§ 2. Термодинамика изопроцессов

Начнем рассматривать приложения первого начала термодинамики к анализу процессов в самой наглядной и доступной модельной системе - идеальном газе.

В изохорном процессе каждая из элементарных работ равна нулю, так как в этом процессе . Тогда, согласно первому началу термодинамики, в изохорном процессе все сообщенное системе количество теплоты расходуется на изменение ее внутренней энергии:

. (3.2.1)

Из последнего выражения следует, что в изохорном процессе количество теплоты можно рассматривать как функцию состояния.

Для нагревания различных тел на одинаковое количество градусов, необходимо затратить различные энергии. Поэтому вводят величину, показывающую, какое количество теплоты нужно сообщить телу для его нагревания на один градус, называемую теплоемкостью

. (3.2.2)

Терминология не отражает физической сути введенной величины, так как тело не может быть емкостью для теплоты, оно является только емкостью для энергии. Данный термин существует в терминологическом аппарате физики, появившись во времена господства теории теплорода.

Теплоемкость может быть отнесена к любому количеству вещества. Отнесенная ко всему телу, теплоемкость тела определяется по формуле (3.2.2). Количество теплоты, необходимое для нагревания на один градус одного килограмма вещества называется удельной теплоемкостью:

. (3.2.3)

Теплоемкость одного моля - молярная теплоемкость:

. (3.2.4)

Далее мы будем рассматривать все процессы для одного моля вещества, поэтому речь будет идти именно о молярной теплоемкости.

Для теплоемкости в изохорном процессе можно записать

, (3.2.5)

где i– число степеней свободы молекулы газа (в случае идеального газа i = 3). Откуда

, (3.2.6)

. (3.2.7)

С другой стороны, при изобарном процессе (3.1.12) , а с учетом (3.1.10)

. (3.2.8) Принимая во внимание, что , можно записать

, или , (3.2.9) откуда теплоемкость при изобарном процессе

. (3.2.10)

Уравнение

(3.2.11) носит название уравнение Майера.

§ 3 Применение первого начала термодинамики к изопроцессам

Будем рассматривать квазиравновесные процессы, т.е. такие, которые идут настолько медленно, что характерное время установления внутреннего равновесия много меньше времени наблюдения за протекающим процессом . К таким процессам может быть применено первое начало термодинамики. Проанализируем с этой точки зрения квазиравновесные процессы в идеальном газе, то есть процессы в системах, уравнением состояния которых является уравнение Менделеева-Клапейрона.

Пусть процесс идет без теплообмена с окружающей средой, то есть система является адиабатически изолированной. Процессы происходящие в такой системе, называются адиабатными процессами, при этом . Для обеспечения этого условия процесс должен идти быстро. Противоречит ли это условию квазиравновесности процесса? Введем время установления равновесия системы с окружающей средой . О квазиравновесном адиабатном процессе можно говорить, только когда .

Предположим, что рассматриваемый процесс удовлетворяет указанному условию и, следовательно, к его анализу применимо первое начало термодинамики, которое в данном случае принимает вид

, (3.3.1)

т.е. при адиабатном процессе работа совершается системой за счет убыли ее потенциальной энергии, то

. (3.3.2)

Теплоемкость системы в адиабатном процессе равна нулю. Это относится к термодинамической системе любой природы.

Введем в рассмотрение идеальный газ, используем выражение (3.3.2) и уравнение состояния идеального газа

Разделив переменные, получим

. (3.3.3)

После интегрирования уравнения (3.3.3) с учетом уравнения Майера (3.2.11) приходим к уравнению адиабаты в координатах (V,T), связывающему температуру и объем идеального газа в адиабатном процессе:

, (3.3.4)

где величина называется показателем адиабаты и равна отношению молярных (или удельных) теплоемкостей газа при постоянном давлении и постоянном объеме.

Используя уравнение Менделеева - Клапейрона можно записать уравнение адиабаты через две другие пара параметров состояния

, (3.3.5)

. (3.3.6)

Найдем выражение для работы, совершаемой идеальным газом в адиабатном процессе при переходе из состояния 1 с параметрами в состояние 2 c параметрами .

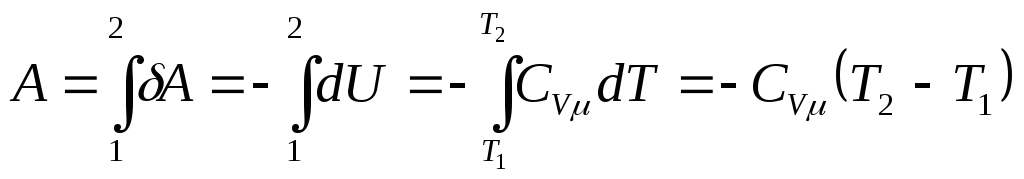. (3.3.7)

Поскольку численное значение работы и ее знак удобно определять по графику процесса, изображенного в координатах , адиабату часто изображают именно в этих координатах. На рис. 3.3.1 изображены изотерма и адиабата для равных масс идеального газа.

Б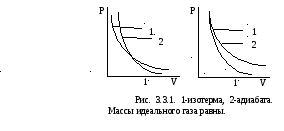ольшая крутизна адиабаты по сравнению с изотермой может быть объяснено из термодинамических представлений. Пусть изотермическое и адиабатное расширение начинаются из одного и того же состояния. В изотермическом процессе давление уменьшается за счет уменьшения объема, а в адиабатном процессе – за счет уменьшения объема и уменьшения средней кинетической энергии молекул, то есть быстрее, чем в изотермическом процессе. Рассуждая аналогично в случае начала изотермического и адиабатного сжатия из одного и того же состояния, приходим к выводу, что увеличение давления в адиабатном процессе идет медленнее.

Как можно показать, теплоемкость в изотермическом процессе равна бесконечности

при T = const, (3.3.8) при постоянном давлении и при постоянном объеме теплоемкости имеют некоторые конечные значения

, , (3.3.9) в адиабатном процессе теплоемкость равна нулю, т.к. .

Рассмотрим теперь процессы с промежуточными значениями теплоемкости, которая в течение процесса не изменяется . Процессы, идущие при постоянной теплоемкости, называются политропическими процессами. Пусть адиабатный процесс, совершаемый над одним молем идеального газа является квазиравновесным.

Согласно первому началу термодинамики для рассматриваемого случая получаем

, (3.3.10) где при политропических процессах. С учетом

, откуда .

Из уравнения Майера , следовательно

Величина называется показателем политропы. Тогда

. (3.3.11)

Интегрируя правую и левую части (метод разделения переменных), получим

или

(3.3.12)

- уравнение политропы. С помощью уравнения Менделеева-Клапейрона его можно записать в виде:

. (3.3.13)

. (3.3.14)

Очевидно, что

при С = 0; n = γ; — уравнение адиабаты;

при С = ∞; n = 1; — уравнение изотермы;

при С = С_р; n = 0; P = Const — уравнение изобары;

при C = C_v; n = ; , но , следовательно, V = Const — уравнение изохоры.

Все изопроцессы являются частными случаями политропического процесса.