Теорема 3.1.1 Рассмотрим систему уравнений

Пусть функции удовлетворяют условиям Липшица своими аргументами. Тогда существует единственное решение = в окрестности , удовлетворяющее начальным условиям . Более того, это решение является непрерывной функцией от начальных условий (of the initial conditions). Если , где - параметр и каждое также удовлетворяет условию Липшица равномерно в в окрестности и непрерывна в , то те же самые условия справедливы во всей окрестности 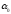. Кроме того, решение является непрерывной функцией в этой окрестности.

Уникальность означает, что для дифференциального уравнения, удовлетворяющего условиям Липшица, решения задачи Коши не пересекаются друг с другом.

Пример Рассмотрим следующее уравнение

.

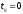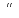
Пусть и Также и являются решениями исходной задачи. Функция не удовлетворяют условию Липшица в окрестности нуля.

Теорема 3.1.1. устанавливает существование единственного решения для некоторой окрестности . Это значит, что теорема обеспечивает только локальное существование теоремы.

Пример Рассмотрим следующее уравнение

.

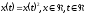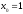Пусть и . Тогда 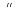является решением исходной задачи. С другой стороны решение этого дифференциального уравнения не существует для . Этот пример показывает, что глобальное существование решений нуждается в тщательном исследовании, когда кто-то находит локальное решение.

Понятие устойчивости определяется следующим образом.

Определение 3.1.4 Рассмотрим систему

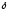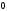Решение , определенное на [] стабильна, если для любого заданного существует >такое, что если есть любой вектор, удовлетворяющий <, то решение с исходным решением существует на и удовлетворяет <, . Стабильность, определенная выше, называется стабильностью Ляпунова или решением стабильности(стабильным решением). [how small is the permitted deviation measured by, there exists a nonzero tolerance, measured by 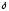, in the initial conditions when the system is activated, allowing it to run satisfactorily]

Пример Общим решение , где <есть 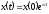. Это решение устойчиво. Как

мы можем выбрать , чтобы гарантировать устойчивость решения.

Другим свойством динамической системы является то, что частное решение может стать менее стабильным с течением времени. Вполне возможно, что чувствительность системы к нарушениям может увеличиться на неопределенное время, хотя со временем она остается технически стабильной, этот признак состоит в том, что, в то время как уменьшается до нуля, увеличивается. Если решение стабильно для и из определения 3.14 не зависит от , то решение равномерно стабильно (устойчиво) на . Любые устойчивые решения автономной системы равномерно стабильны, если система инвариантна относительно преобразования времени. Еще одно свойство – асимптотическая стабильность.

Определение 3.1.5. Решение равенства асимптотически стабильно, если (а) оно стабильно и (b) существует >такое, что если <, тогда , при . Это глобально асимптотическое решение, если может быть выбрано сколько угодно большим.

Очевидно, что решение при <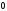есть глобально асимптотическое решение.

На рисунках 3.1.2a и 3.1.2b (для двумерной динамики) равновесие устойчиво. Это значит, что все решения, начинающиеся с «Достаточно», близки к равновесной пребывания и находятся рядом с ней. Следует отметить, что траектория решения не должна подходить к точке равновесия , как показано на рисунке 3.1.2b. Если точка равновесия асимптотически устойчива, траектории, «достаточно близкие» к ней, должны не только оставаться закрытыми, но и должны оставаться «близкими», но в конечном итоге должны стремиться к нему так, как . Это случай для траектории на рисунке 3.1.2a, но не для той же траектории, изображенной на рисунке 3.1.2b. Очевидно, что свойство асимптотической стабильности сильнее свойства стабильности.

Определение 3.1.6. Решение к неустойчиво, если для любого достаточно малого и для любых существует решение такое, что (a) и (b) при некоторых .

Нестабильность также упоминается как нестабильность Ляпунова.

Пример Общим решением при есть . Из мы видим, что если мы всегда можем выбрать , удовлетворяющее . Таким образом, уравнение неустойчиво.

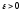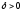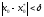Определение 3.1.7. Решение динамической системы будет орбитально устойчивым, если для любого заданного существует такое, что если , тогда

, , для каждого

Не следует путать понятие устойчивости и орбитальной стабильности. Рисунок 3.1.3 является хорошим примером. Предположим, что C и D - две орбиты разных периодов. Хотя расстояние между ними остается ограниченным все время, расстояние между двумя точками 1 и 2 на двух орбитах может увеличиться вследствие сдвига фаз, индуцированных разницей между периодами. Таким образом, фаза один не обязательно должна быть устойчива, даже если С орбитально устойчива.

Эти определения для применимы к автономной системе .

Определение 3.1.8. Периодическое решение динамической системы, непрерывной во времени, в пределах которого нет других периодических решений, называется предельным циклом.

Упражнение 3.1.

1. Для общего двумерного уравнения

,

найти константу Липшица для функции с точки зрения a, b, c и d.

3.2 Устойчивость равновесия автономных уравнений

Из определений в предыдущем разделе мы видим, что устойчивость точки равновесия из скалярного дифференциального уравнения

(3.2.1)

является локальным свойством потока вблизи равновесия. Следующая теорема гласит, что при определенных условиях устойчивость свойств можно определить из линейной аппроксимации функции вблизи .

Теорема 3.2.1 Предположим, что 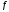- функция класса и - точка равновесия , то есть . Предположим также, что . Тогда точка равновесия асимптотически устойчива, если и неустойчива, если .

Линейное дифференциальное уравнение называется линейным уравнением вариации или линеаризацией векторного поля относительно своей точки равновесия .

Поскольку точка равновесия из асимптотически устойчива, если и нестабильна, если , мы видим, что Теорема 3.2.1 утверждает, что если , тип устойчивости точки равновесия из есть таким же, как и тип устойчивости точки равновесия в начале его линеаризованного векторного поля. Следует отметить, что условие является важным. Точка равновесия из называется гиперболическим равновесием (точкой гиперболического равновесия), если . Если , то называется негиперболической или вырожденной точкой равновесия. Когда равновесие вырождено, его устойчивость определяется более высокими членами разложения Тейлора функции при . Например, происхождение неустойчивого равновесия для 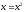, но это асимптотически устойчивое равновесие при .

Пример Монетарная модель Кагана.

Модель гиперинфляции Кагана описывается парой уравнений

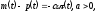
где - натуральный логарифм номинальной денежной массы (), - натуральный логарифм уровня цен (), а - ожидаемый уровень инфляции. В этой модели производство и реальная процентная ставка являются фиксированными и эффект богатства игнорируется. Первое уравнение описывает непрерывное равновесие на денежном рынке, а второе уравнение выражает обычную форму адаптивной гипотезы об ожидаемом уровне инфляции. Коэффициент

интерпретируется как полу-эластичность спроса. Он измеряет процентное изменение спроса на деньги в процентных пунктах изменения ожидаемого уровня инфляции. Предположим, номинальная денежная масса остается постоянной, из первого уравнения получаем, что . Подставляя первое уравнение и во второе, получаем

.

Мы делаем вывод, что корректировка цен устойчива тогда и только тогда, когда . Это соотношение подчеркивает компромисс (изменение одного показателя за счет другого) между полу-эластичностью спроса на деньги по отношению к инфляционным ожиданиям и скоростью адаптации инфляционных ожиданий. Высокая чувствительность спроса на денежную функцию совместима с устойчивостью, только если инфляционные ожидания достаточно адаптируются к прошлым темпам инфляции.

Пример Ловушки бедности, генерируемые в модели Солоу.

Король и Ребело пытались объяснить ловушки бедности в рамках неоклассической теории роста с помощью функции полезности, в которой есть прожиточный минимум на душу населения и эластичность межвременной замены меняется с течением времени. Модель имеет два положения равновесия – типа Солоу и неустойчивость стационарного состояния на уровне акционерного капитала, сопоставимого с величиной прожиточного потребления.

Проиллюстрируем этот подход на основе Рос (Ros (2000: 60-62)). Модель начинается с функции потребления

(3.2.2)

где и соответственно потребление на душу населения и доход на душу населения в момент времени , - прожиточный минимум на душу населения, - соотношение капитала и труда в соответствии с уровнем прожиточного минимума, - норма амортизации капитала, - склонность к потреблению без учета прожиточного минимума. ОтменаПрослушатьНа латиницеКогда доход на одного рабочего на уровне прожиточного минимума равен амортизации основного капитала, то есть . Соответствующая норма сбережений – это

(3.2.3)

где . Здесь - склонность к сбережениям не из прожиточного минимума. В соответствии с определениями, параметр может быть положительным или отрицательным. Если , положительно, подразумевая то, что по мере роста доходов сбережения уменьшаются. Сбережения являются нелинейной функцией от уровня доходов на душу населения. Норма сбережений растет вместе с доходом на душу населения, если предельная склонность к потреблению без учета прожиточного минимума меньше, чем средняя склонность к потреблению с учетом прожиточного минимума.

В противном случае, норма сбережений имеет тенденцию падать по мере увеличения дохода выше прожиточного минимума. Подставляя уравнение (3.2.3) в основное уравнение

,

которое по дает

(3.2.4)

в котором - фиксированный прирост населения. Мы называем вышеописанную модель обобщенной моделью Солоу с ловушками бедности. Проверьте, что эта модель может иметь два равновесия, как показано на рисунке 3.2.1 при .

В случае, когда , равновесие при высоком уровне похоже на устойчивое состояние в модели Солоу. Другое – на уровне прожиточного минимума. Это часто упоминается как ловушка бедности, но такое состояние неустойчиво. Экономическая система не будет оставаться там долгое время. Бедность не может быть устойчива при надлежащих нарушениях, например, внешней поддержке и торговли. Эта ловушка происходит потому, что при низком уровне соотношения капитала и труда доход на душу населения едва ли достаточен и сбережения опускаются ниже амортизации. Если экономика переживает такой вид бедности, то легко начать быстрое развитие, потому что однажды соотношение труда и капитала станет выше, чем уровень , он будет быстро расти в направлении устойчивого равновесия. Как только он достигает высокого уровня жизни, он в ловушке, поскольку это стабильное состояние. Модель имеет только одно условие равновесие – состояние неустойчивой бедности, когда , то есть, Такая ситуация имеет место, когда норма сбережений является слишком низкой или когда прожиточный минимум на душу является слишком низким. Если экономика характеризуется политической и социальной нестабильностью, то она имеет низкий уровень сбережений. При таких обстоятельствах, народ вряд ли может сделать какой-либо прогресс в экономическом развитии.