"Криволинейные интегралы"

 

Криволинейным интегралом II рода от функций  и  по плоской кривой  от точки  к  точке называют предел , где точки  – точки, которые разбивают участок кривой  от точки  до точки  на  частей, а  и  – приращения соответствующих координат при переходе от точки  к точке . Криволинейный интеграл II рода обозначают:  или . Направление по кривой  от точки  до точки  называется направлением интегрирования. Если кривая  пространственная, то криволинейный интеграл II рода от трех функций , ,  определяется аналогично:

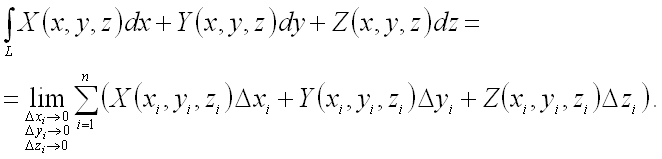
Свойства криволинейного интеграла II рода

1. Криволинейный интеграл определяется подынтегральным выражением, формой кривой интегрирования и указанием направления интегрирования. При изменении направления интегрирования криволинейный интеграл меняет знак. 2. Если участок кривой  от точки  до точки  разбить точкой на две части  и , то непосредственно из определения криволинейного интеграла II рода следует, что .

Если криволинейный интеграл II рода вычисляется по замкнутой кривой , то его называют криволинейным интегралом II рода по замкнутому контуру и обозначают . При вычислении криволинейного интеграла II рода по замкнутому контуру необходимо учитывать направление обхода замкнутой кривой  (против часовой стрелки или по часовой стрелке).

Вычисление криволинейного интеграла II рода

Если кривая  задана уравнениями в параметрической форме: где функции  и  непрерывны и имеют непрерывные производные  и , и, кроме того, функции  и  также непрерывны как функции параметра  на отрезке , то криволинейный интеграл II рода может быть вычислен по формуле: , где точкам  и  соответствуют значения  и  параметра . Аналогично вычисляется криволинейный интеграл II рода по пространственной кривой , заданной уравнениями в параметрической форме .

 приложения криволинейных интегралов       Длина кривой 

     Масса кривой 

( - плотность кривой).

     Координаты центра масс 

     Работа 

     Работа силы  вдоль кривой l:

Основные понятия об обыкновенных дифференциальных уравнения (оду)

Дифференциальное уравнение - это уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значения её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, ее производные и независимые переменные.

Все дифференциальные уравнения можно разделить на обыкновенные дифференциальные уравнения(ОДУ), в которые входят только функции (и ихпроизводные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Порядком или степеньюдифференциального уравнения называется наибольший порядок производных, входящих в дифференциальное уравнение.

Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени. Формулировка второго закона Ньютона для материальной точки дает простейший пример обыкновенного дифференциального уравнения второго порядка с неизвестной функцией координат точки и временем, выступающим в роли независимой переменной.

Обыкновенное дифференциальное уравнение (ОДУ)  -ого порядка — это уравнение вида

где  — неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от независимой переменной  , штрих означает дифференцирование по  .

Решением дифференциального уравнения называется  раз дифференцируемаяфункция  , удовлетворяющая уравнению во всех точках своей области определения. Обычно существует целое множество таких функций (такое параметризованное семейство рещений называется общим решением дифференциального уравнения), и для выбора одного из них требуется наложить на него дополнительные условие: например, потребовать, чтобы решение принимало в данной точке данное значение. Полученное единственное решение называется частным решением. Общее решение обыкновенного дифференциального уравнения  -ого порядка может быть выражено в виде

где  ,  - произвольные постоянные. Если общее решение задано в неявном виде выражением

то это выражение называют общим интегралом дифференциального уравнения.

   Уравнения с разделенными переменными 

     Общий интеграл 

     Уравнение с разделяющимися переменными 

     Общий интеграл