
ЛП-метод-каЛуценко
.pdf
ФЕДЕРАЛЬНОЕ АГЕНСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение высшего профессионального образования
«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»
Кафедра «Математика и моделирование»
М.М. Луценко
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
РЕШЕНИЕ ЗАДАЧИ
Методические указания и варианты индивидуальных заданий для студентов заочного факультета
САНКТ-ПЕТЕРБУРГ
2006
УДК 512.8
М.М.Луценко
Линейное программирование. Решение задачи. Методические указания и варианты индивидуальных заданий для студентов заочного факультета, – СПб.: Петербургский государственный университет путей сообщения, 2006, 22 с.
Содержание пособия соответствует разделам математического программирования, изучаемым студентами в 3 семестре. Пособие предназначено для студентов специальностей УПП заочного факультета ПГУПС.
Рецензент: профессор В.В. Гарбарук (кафедра «Высшая математика» ПГУПС)
© М.М.Луценко © Петербургский государ-
ственный университет
2

Постановка задачи
Главным объектом изучения в линейном программирование является задача, которая в наиболее общей форме формулируется следующем образом.
Задача. Найти экстремум линейной функции F, если ее аргументы удовлетворяют некоторым ограничениям.
Настоящие методические указания посвящены анализу задачи линейного программирования, даны ее различные формы записи и указаны некоторые способы ее решения.
Каждый студент должен будет сделать для своей задачи все ниже перечисленные действия.
1.Записать задачу в матричной форме
2.Записать каноническую задачу.
3.Решить задачу геометрически.
4.Найти начальный базисный план с помощью искусственных переменных.
5.Решить задачу симплекс-методом.
6.Написать двойственную задачу к искомой в матричной и развернутой формах.
7.Найти решение двойственной задачи и доказать его оптимальность с помощью теоремы двойственности.
Варианты задач и пример решения указаны в конце этих указаний.
Матричная и развернутая формы задачи линейного программирования
В этом параграфе мы сравним две формы записи задачи линейного программирования.
Определение 1. Следующая задача называется стандартной задачей линейного программирования.
Задача 1. Найти
F |
ct x |
max , |
(1) |
Ax |
b , x |
0 , |
(2) |
где A – матрица системы ограничений, имеющая m строк и n столбцов, b – столбец из m элементов; c, x – столбцы из n элементов. Таким образом, эти матрицы имеют вид
a1,1 |
a1,2 |
a1,n |
|
b1 |
|
c1 |
|
x1 |
|
|
|
a2,1 |
a2,2 |
a2,n |
, b |
b2 |
, c |
c2 |
, x |
x2 |
. |
(3) |
|
A |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||
am,1 |
am,2 |
am,n |
|
bm |
|
cn |
|
xn |
|
|
|
В развернутой форме эта стандартная задача линейного программирования может быть записана в следующем виде.
Задача 1’. Найти максимум линейной функции
F ct |
x c x c |
x |
2 |
c x |
, |
|
(1 ) |
||
|
1 |
1 2 |
|
|
n n |
|
|
|
|
при ограничениях: |
|
|
|
|
|
|
|
|
|
a1,1x1 |
a1,2 x2 |
a2,n xn |
b1 , |
|
|
|
|||
a2,1 x1 |
a2,2 x2 |
a2,n xn |
b2 , |
x1, x2 , xn |
0 . |
(2 ) |
|||
|
|
||||||||
|
|
|
|
||||||
am,1x1 |
am,2 x2 |
am,n xn |
bm , |
|
|
|
|||
3

Определение 2. Решением этих задач называется матрица (упорядоченный на-
бор чисел) x *t (x * , x * , x * ), удовлетворяющая системе ограничений (2) и |
||
1 |
2 |
n |
обеспечивающая максимальное значение функции (1). Иногда это решение называется оптимальным планом задачи. Значение функции на оптимальном плане обозначается
Fmax F (x*) .
Определение 3. Линейная функция F задачи 1 называется целевой функцией, а множество D решений системы (2) – множеством допустимых решений (планов) этой задачи.
Пример 1. Записать задачу линейного программирования (1), (2) с матрицами
|
5 |
6 |
30 |
7 |
|
x1 |
|
A |
4 |
3 |
; b 20 ; c |
; x |
|||
2 |
x2 |
||||||
|
3 |
1 |
28 |
|
|
|
в развернутой форме (1 , 2 ) .
Решение. В развернутой форме задача формулируется следующим образом.
Найти максимум функции F |
ct x 7x |
2x |
при ограничениях |
|
|
|
1 |
2 |
|
5x1 |
6x2 |
30, |
|
|
4x1 |
3x2 |
20, |
|
x1, x2 0 . |
3x1 x2 28,
Пример 2. Записать следующую задачу линейного программирования в матричной форме.
Минимизировать линейную функцию F |
3x1 2x2 при ограничениях |
||
x1 |
x2 |
4, |
|
x1 |
x2 |
0, |
x1, x2 0 . |
3x1 |
x2 |
5, |
|
Решение. Для того чтобы записать эту задачу в матричной форме (1, 2), изменим неравенства в ограничениях задачи так, чтоб они имели одинаковый знак. Для этого умножим первое неравенство на –1. Мы получим следующую систему ограничений задачи:
|
|
|
x1 |
x2 |
4, |
|
|
|
|
|
|
|
|
x1 |
x2 |
0, |
|
|
|
|
|
|
|
|
3x1 |
x2 |
5, |
|
|
|
|
|
Тогда в матричной форме задача примет вид |
|
|
|
|
|
|||||
|
|
F |
ct x |
max , |
|
|
|
|
||
|
|
|
Ax b , x 0 , |
|
|
|
|
|||
где |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
4 |
|
3 |
|
|
x1 |
|
|
A |
1 |
1 ; b |
0 |
; c |
; |
x |
. |
|||
2 |
x2 |
|||||||||
|
2 |
1 |
5 |
|
|
|
|
|||
|
|
|
|
|
|
|
||||
4

Геометрическое решение задачи линейного программирования
Для того чтобы решить задачу линейного программирования геометрически, построим множество решений системы ограничений. Любая прямая a1x1 a2 x2 p
разбивает плоскость на две полуплоскости. Для точек M (x1, x2 ) одной из полуплоско-
стей выполняется неравенство a1x1 |
a2 x2 |
p , а для |
точек другой полуплоскости |
||
противоположное неравенство a1x1 |
a2 x2 |
p . Если |
ограничением |
задачи |
будет |
система неравенств, то множеством |
допустимых решений D этой |
задачи |
будет |
||
выпуклое многоугольное множество, полученное как пересечение полуплоскостей, каждая из которых является решением соответствующего неравенства системы.
Построим теперь линии уровня функции F c1 x1 c2 x2 . Очевидно, что это будут параллельные линии c1 x1 c2 x2 p , перпендикулярные нормальному вектору n (c1 ,c2 ) . Следовательно, при параллельном перемещении линии уровня в направ-
лении вектора n значение целевой функции F будет возрастать, а противоположном убывать. Свое максимальное значение функция F примет на «последней» общей точке множества допустимых решений и соответствующей линии уровня при ее параллельном переносе в направлении вектора n .
Пример 3. Решить следующую задачу линейного программирования геометриче-
ски.
F ct |
x 7x |
2x |
max , |
|
(4) |
|
|
|
1 |
2 |
|
|
|
при ограничениях |
|
|
|
|
|
|
5x1 |
6x2 |
30, |
|
|
|
|
4x1 |
3x2 |
20, |
x1, x2 |
0 . |
(5) |
|
3x1 |
x2 |
28, |
|
|
|
|
Решение. Найдем множество |
D решений неравенств. |
Для этого построим три |
||||
прямые: |
|
|
|
|
|
|
5x1 |
6x2 |
30, |
|
|
|
(I ) |
4x1 |
3x2 |
20, |
|
|
|
(II ) |
3x1 |
x2 |
28. |
|
|
|
(III ) |
Прямая (I ) разбивает плоскость на две полуплоскости. Стрелочками отметим ту |
||||||
полуплоскости, которая удовлетворяет неравенству |
5x1 6x2 |
30 . Для этого дос- |
||||
таточно проверить хотя бы одну точку этой полуплоскости, например, начало координат O(0,0) . Пересечение полуплоскостей составит множество допустимых решений задачи D.
5

Построим теперь линии уровня функции F, т.е прямые 7x1 |
2x2 |
p |
для раз- |
личных p. На рисунке показана прямая, соответствующая значению |
p |
14 . |
На части |
( III ) |
l |
( I ) |
|
|
|
x2 |
|
|
l0 |
|
|
 ( II )
( II )
n |
D |
Q(8,4) |
|
этой прямой, лежащей внутри этой области, значение функции F равно 14.
Параллельно переместим эту прямую в направлении вектора n . Свое наибольшее на множестве D значение функция F примет в вершине многоугольника точке Q . Для того чтобы
найти ее координаты достаточно решить систему уравнений:
4x1 3x2 20,
|
x1 |
|
3x1 |
x2 |
28. |
|
|
|
|
Откуда |
мы |
находим |
|
p =14 |
p =64 |
x1 |
8 , x2 |
4 . Итак, мак- |
||
|
симальное на множестве D |
|||||
|
|
|||||
|
|
значение функции F равно |
||||
|
|
Fmax |
7 8 |
2 |
4 |
64 , |
которое она принимает в точке с координатами x1 |
8 , x2 4 . |
|
|
|
|
|
Построение симплекс-таблицы
Определение 4. Задача линейного программирования называется канонической, если она имеет следующий вид.
Задача 2. Найти минимум линейной функции:
F c |
ct |
|
x |
c |
c x |
c x |
c x |
, |
(6) |
0 |
|
|
|
0 |
1 1 |
2 2 |
n |
n |
|
при ограничениях |
|
|
|
|
|
|
|
|
|
a1,1x1 |
|
|
a1,2 x2 |
a2,n xn |
b1, |
|
|
||
a2,1x1 |
|
|
a2,2 x2 |
a2,n xn |
b1, |
|
(7) |
||
|
|
|
|
||||||
|
|
|
|
||||||
an,1x1 |
|
|
an,2 x2 |
an,n xn |
b1, |
|
|
||
|
|
|
|
x1, x2 , xn |
0 , |
|
|
|
|
или в матричной форме |
|
|
|
|
|
|
|
|
|
F |
c |
|
ct x |
min , |
|
|
|
(8) |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
Ax |
b , |
x 0. |
|
|
|
(9) |
|
Определение 5. Мы будем говорить, что задача линейного программирования (1,2) сведена к некоторой канонической задаче линейного программирования (возможно с другим числом переменных и ограничений), если по решению первой задачи можно построить решение второй задачи и наоборот.
Пример 4. Свести задачу линейного программирования
6

F ct x 7x |
2x |
max , |
|
1 |
2 |
|
|
при ограничениях |
|
|
|
5x1 |
6x2 |
30, |
|
4x1 |
3x2 |
20, |
(10) |
3x1 x2 28, x1, x2 0 ,
к канонической задаче.
Перенесем члены неравенств в одну часть так, чтобы полученные выражения были неотрицательны:
30 |
5x1 |
|
6x2 |
|
0, |
|
20 |
4x1 |
|
3x2 |
|
0, |
|
28 3x1 |
x2 |
|
0. |
|
||
Введем дополнительные переменные x3 , |
x4 , x5 по формулам: |
|
||||
x3 |
30 |
5x1 |
6x2 , |
|
||
x4 |
20 |
|
4x1 |
3x2 , |
(11) |
|
x5 |
28 |
|
3x1 |
|
x2 . |
|
Таким образом, каждому решению |
xt |
|
(x , x |
2 |
) системы неравенств (10) будет |
|
|
|
|
1 |
|
|
|
соответствовать решение (x1 , x2 , x3 , x4 , x5 ) |
системы уравнений (11), причем все его |
|||||
компоненты будут неотрицательны. И наоборот каждому неотрицательному решению
(x , x |
2 |
, x |
3 |
, x |
4 |
, x |
5 |
) |
системы (11) будет соответствовать решение |
xt |
(x , x |
2 |
) системы |
1 |
|
|
|
|
|
|
1 |
|
|||||
(10). |
|
|
|
|
|
|
|
|
|
|
|
|
|
Если функция F принимает в некоторой точке максимальное значение, то в этой точке функция (–F) принимает свое минимальное значение. Причем эти значения будут равны с точностью до знака. Таким образом, вместо максимума функции
F |
7x1 |
2x2 на множестве D можно искать на этом множестве минимум функции |
F1 |
F |
7x1 2x2 . |
Таким образом, искомая задача может быть сведена к следующей задаче линейного программирования:
F1 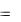 7x1 2x2 min ,
7x1 2x2 min ,
при ограничениях
5x1 6x2 x3 30,
4x1 3x2 x4 20,
3x1 x2 x5 28, x1 , x2 , x3 , x4 , x5 0 .
По оптимальному решению первоначальной задачи легко найти оптимальное решение канонической задачи.
7

Минимальное значение функции F1,min 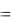 64 , в точке с координатами:
64 , в точке с координатами:
x1 8 , x2 4 , x3 30 5  8 6
8 6  4 46 , x4 20 4 8 3 4 0 , x5 28 3 8 4 0 .
4 46 , x4 20 4 8 3 4 0 , x5 28 3 8 4 0 .
Определение 6. Набор из m различных переменных системы уравнений (7) называется базисным, если все переменные из этого набора могут быть выражены только через оставшиеся переменные с помощью элементарных преобразований системы. Переменные, входящие в этот набор, называются базисными, а остальные свободными.
Определение 7. Решение системы (7) называется базисным (опорным планом), если значения всех свободных переменных равны нулю.
Пример 5. Найти базисное решение системы:
a1,1x1 |
a1,2 x2 |
x3 |
b1, |
|
a2,1x1 |
a2,2 x2 |
x4 |
b2 , |
(12) |
a3,1x1 |
a3,2 x2 |
x5 |
b3. |
|
Решение. В этой системе уравнений за базисные переменные можно взять переменные x3 , x4 , x5 , а за свободные x1 , x2 , так как первые легко выражаются через по-
следние. Итак, базисным решением этой системы будет набор чисел (0,0,b1 ,b2 ,b3 ) .
Определение 8. Симплекс-таблицей для канонической задачи (6), (7) называется следующая таблица:
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 |
||
|
|
|
|
|
|
|
x |
|
x2 |
|
.... |
xn |
b |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
a1,1 |
|
a1,2 |
|
.... |
a1,n |
b1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
a2,1 |
|
a2,1 |
|
.... |
a2,n |
b2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.... |
|
.... |
|
.... |
|
.... |
.... |
.... |
|
|
|
|
|
|
xi |
|
am,1 |
|
am,2 |
|
|
am,n |
bm |
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
c1 |
|
c2 |
|
.... |
cn |
c0 |
|
Здесь |
xi |
, xi |
, , xi |
имена базисных переменных. Последняя строка таблицы соот- |
||||||||||
|
1 |
2 |
m |
|
|
|
|
|
|
|
|
|
|
|
ветствует равенству F c1x1 |
c2 x2 |
|
|
cn xn |
c0 . |
|
|
|||||||
Мы будем называть эту таблицу базисной, если в столбцах помеченных перемен- |
||||||||||||||
ными |
xi |
, xi |
, , xi |
стоят только нули, |
за исключением строки помеченной той же |
|||||||||
|
1 |
2 |
m |
|
|
|
|
|
|
|
|
|
|
|
переменной, где стоит 1.
В дальнейшем мы будем иметь дело только с базисными симплекс-таблицами. Каждая базисная симплекс-таблица порождает некоторое базисное решение. В нем значения выделенных базисных переменных равны соответствующим свободным членам, а значения остальных переменных равны нулю.
Легко убедиться в верности следующих условий допустимости и оптимальности базисных решений
Условие допустимости.
Базисное решение, порождаемое базисной симплекс-таблицей, допустимо, если
все элементы столбца свободных членов неотрицательны: bi 0 , i 1,m.
8

Условие оптимальности.
Допустимое базисное решение, порождаемое базисной симплекс таблицей, оптимально, если все числа, стоящие в последней строке, неположительные, за исключе-
нием, быть может, числа c0 .
Таким образом, мы выделили класс симплекс-таблиц, по которым легко построить оптимальное базисное решение.
Пример 6. Записать следующую задачу в форме симплекс таблицы в базисе переменных x3 , x4 , x5 , а также условия допустимости и оптимальности соответствующего базисного решения.
F c0 c1 x1 c2 x2 |
min, при ограничениях (12) и x1, x2 , x3 , x4 , x5 0 . |
Решение. Соответствующая симплекс таблица будет иметь вид:
|
|
|
|
|
Таблица 2 |
|
|
x1 |
x2 |
x3 |
x4 |
x5 |
b |
x3 |
a1,1 |
a1,2 |
1 |
0 |
0 |
b1 |
x4 |
a2,1 |
a2,1 |
0 |
1 |
0 |
b2 |
x5 |
am,1 |
am,2 |
0 |
0 |
1 |
b3 |
F |
c1 |
c2 |
0 |
0 |
0 |
c0 |
Базисным решением задачи будет матрица xt (0,0,b ,b ,b ) . Оно будет допус- |
||
1 |
2 |
3 |
тимым, если b1 ,b2 ,b3 0 и оптимальным, если c1 , c2 0 . При выполнении этих условий минимальное значение функции F будет равно c0 .
Преобразование симплекс таблиц
Сформулируем теперь правила преобразования симплекс таблиц. Так как каждой таблице можно сопоставить систему линейных алгебраических уравнений, то эти правила будут аналогичны тем правилам, которые известны из теории преобразования систем линейных уравнений. А целью этих преобразований будет получение такой таблицы, для которой выполняются вышеуказанные условия оптимальности.
Все наши действия имеют также геометрическую интерпретацию. Каждому базисному решению задачи соответствует вершина выпуклого многогранного множества допустимых решений задачи. А каждому преобразованию симплекс таблицы соответствует переход от одной вершины к другой, уменьшающий значение целевой функции.
Проверка оптимальности и выбор генерального элемента симплекс таблицы
 Если все элементы последней строки таблицы, кроме последнего, неположительные, то таблица порождает оптимальное базисное решение.
Если все элементы последней строки таблицы, кроме последнего, неположительные, то таблица порождает оптимальное базисное решение.
 За генеральный столбец берётся тот столбец таблицы, кроме последнего, в последней строке которого стоит положительный элемент.
За генеральный столбец берётся тот столбец таблицы, кроме последнего, в последней строке которого стоит положительный элемент.
 Если все элементы выбранного генерального столбца, кроме последнего, неположительные, то целевая функция неограниченна на множестве допустимых решений, а задача не имеет оптимального плана.
Если все элементы выбранного генерального столбца, кроме последнего, неположительные, то целевая функция неограниченна на множестве допустимых решений, а задача не имеет оптимального плана.
 За генеральную строку берется та строка таблицы, кроме последней, в которой отношение свободного члена к положительному элементу генерального столбца наименьшее.
За генеральную строку берется та строка таблицы, кроме последней, в которой отношение свободного члена к положительному элементу генерального столбца наименьшее.
9

Генеральный элемент таблицы помечается знаком *.
Составление новой симплекс таблицы.
 Имена всех базисных переменных сохраняются за исключением имени генеральной строки. Оно заменяется именем переменной генерального столбца.
Имена всех базисных переменных сохраняются за исключением имени генеральной строки. Оно заменяется именем переменной генерального столбца.
 Элементы генеральной строки делятся на генеральный элемент, и полученные значения заносятся в новую таблицу. В частности, на месте генерального элемента записывается единица.
Элементы генеральной строки делятся на генеральный элемент, и полученные значения заносятся в новую таблицу. В частности, на месте генерального элемента записывается единица.
Остальные элементы генерального столбца заменяются нулями.
Для элемента s исходной таблицы находятся соответствующий ему
элемент генеральной строки q и элемент |
r |
генерального столбца. |
На месте |
||
этого элемента в новой таблице пишется |
|
|
|
|
|
s s |
q |
r |
, |
(13) |
|
p * |
|||||
|
|
|
|||
где p * – генеральный элемент.
Компактно это преобразование таблицы можно записать в виде формулы:
p * |
q |
1 |
q / p * |
|||
|
|
|
q r |
|||
r |
s |
0 |
s |
|
||
|
|
|
||||
|
p * |
|||||
|
|
|
||||
|
|
|
|
|
||
Пример 7. Решить следующую каноническую задачу линейного программирова- |
||||||
ния симплекс-методом. |
|
|
|
|
|
|
F1 |
7x1 2x2 |
|
min , |
|||
при ограничениях |
|
|
|
|
|
|
|
5x1 |
6x2 |
x3 |
30, |
|
|
|
4x1 |
3x2 |
x4 |
20, |
|
|
|
3x1 |
x2 |
x5 |
28, |
|
|
x1, x2 0
Решение. В этой задаче легко выделить базисные и свободные переменные. Полагая значения свободных переменных x1 , x2 нулю, найдем значение базисных перемен-
ных: |
x3 30 , |
x4 20 , |
x5 28 . |
Полученное |
базисное |
решение |
xt |
(0, 0, 30, 20, 28) |
очевидно неотрицательно и, следовательно, допустимо. Соста- |
||||
вим теперь (базисную) симплекс-таблицу в первом столбце, которой указаны имена базисных переменных. (Таблица 3.)
Таблица 3.
|
x1 |
x2 |
x3 |
x4 |
x5 |
b |
x3 |
–5 |
6 |
1 |
0 |
0 |
30 |
x4 |
4* |
–3 |
0 |
1 |
0 |
20 |
x5 |
3 |
1 |
0 |
0 |
1 |
28 |
F1 |
7 |
2 |
0 |
0 |
0 |
0 |
Таблица 4.
|
x1 |
x2 |
x3 |
x4 |
x5 |
b |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
1 |
–3/4 |
0 |
1/4 |
0 |
5 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Эта таблица не порождает оптимальное базисное решение, так как в последней строке стоят два положительных числа. Возьмем одно из них, например 7. Следова-
10
