ЛИТЕРАТУРА

Основная

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сыктывкарский Государственный Университет им. Питирима Сорокина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

05-06 МАТАН.pdf

Скачиваний:

Добавлен:

29.03.2016

Размер:

594.66 Кб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

разрешенные относительно производной. Общий метод введения параметра. Уравнения Лагранжа и Клеро. Простейшие типы уравнений высших порядков, допускающих понижение порядка.

Тема 4. Линейные уравнения высокого порядка.

Линейные уравнения n-го порядка. Свойства решений однородного линейного уравнения,

фундаментальная система решений. Свойства решений неоднородного линейного уравнения, ме-

тод вариации произвольных постоянных.

Тема 5. Линейные уравнения с постоянными коэффициентами.

Построение фундаментальной системы решений однородного линейного уравнения n-го порядка с постоянными коэффициентами. Построение общего решения неоднородного линейного уравнения с постоянными коэффициентами и специальной правой частью.

Тема 6. Системы линейных уравнений первого порядка.

Основные понятия, относящиеся к системам обыкновенных дифференциальных уравнений:

порядок системы, решение системы, нормальная форма системы. Задача Коши для нормальной системы, начальные данные. Достаточные условия существования и единственности решения за-

дачи Коши для нормальной системы. Общее и частное решения нормальной системы. Нормальная система линейных дифференциальных уравнений. Свойства решений нормальной системы линей-

ных однородных уравнений. Свойства решений нормальной системы линейных неоднородных уравнений, метод вариации произвольных постоянных.

Тема 7. Линейные системы с постоянными коэффициентами.

Построение фундаментальной системы решений нормальной системы однородных линей-

ных уравнений с постоянными коэффициентами.

M (x, y)dx

1.В. А. Ильин, Э. Г. Поздняк. Основы математического анализа, т. 2. М.: Наука, 2001. 2.Л. Д. Кудрявцев. Математический анализ, т.1. М.: Высшая школа, 1981, 1988.

3.Б. П. Демидович. Сборник задач и упражнений по математическому анализу. М.: Наука, 2003. 4.А. Ф. Филиппов. Сборник задач по дифференциальным уравнениям. М.: Наука, 1973, 1979, 1985.

Дополнительная

1.Я. С. Бугров, С. М. Никольский. Дифференциальное и интегральное исчисление. М.: Наука, 1980, 1985, 1989.

2.Г. Н. Бергман. Сборник задач по математическому анализу. М.: Наука, 2002, 2005.

166

5.2 Ряды с положительными членами.

Понятие числового ряда. Основные понятия.

Рассматривается числовая последовательность an вещественных (или комплексных) чи-

сел. Сумма первых k ее членов называется k – ой частичной суммой: Sk an .

n 1

Определение. Числовой ряд an называется сходящимся, если существует конечный пре-

n 1
дел последовательности Sk частичных сумм, т.е.		k
дел последовательности Sk частичных сумм, т.е.	S lim	an - сумма числового ряда.
	k	n 1
		n 1

Член an последовательности an называют n - ым членом или общим членом числового

ряда. Если предела последовательности Sk не существует или он бесконечный, то соответст-

вующий числовой ряд называют расходящимся.

Пример 1. Исследовать на сходимость числовой ряд с общим членом an qn

(ряд геометрической прогрессии).

Решение. Воспользуемся формулой суммы k членов геометрической прогрессии:

a (1 qk )

, существует предел S lim Sk

a (1 qk )

. Если

lim

1 q

При q 1

для любого n an

1 и Sk

k и соответствующий ряд расходится.

При

q 1 последовательность Sk

1 k

1 ограничена,

но не имеет предела и ряд

также расходится. Расходимость ряда при

1 следует из неограниченности последовательно-

сти Sk

q(1 qk

)

и, как следствие, отсутствие у нее предела.

1 q

Применяя к Sk критерий Коши для последовательности, получим Критерий Коши для

ряда:

Числовой

ряд an сходится

в том

и только

том

случае,

если

n 1

: m N и n m

am 1 am 2 ... an

Доказательство. Последовательность Sk сходится в том и только в том случае, если к ней

применим критерий Коши: 0

N : m N и n m

Sn Sm

am 1

am 2

... an

Теорема 1. (Необходимое условие сходимости ряда)

167

Если ряд an

сходится, то lim an

0 .

n 1

Доказательство. По критерию Коши 0 N

: n N

Sn 1

Существуют расходящиеся ряды, для которых lim an

0 .

Пример 2. (гармонический ряд).

Доказать, что ряд

расходится.

n 1

Решение. Действительно, S

n S

n 1

...

2n 1

2n 1 1

2n 1 2

для любого n , и критерий Коши для последовательности Sk не выполняется, т.е. ряд расходится.

Упражнения.


1.	Если ряд an	(1) сходится, то ряд an также сходится при любом				.
	n 1			n 1

2.	Если ряды an		(1) и bn	(2) сходящиеся, то ряд (an	bn ) сходящийся.
	n 1		n 1	n 1

Ряды с положительными членами.

Если an 0 для любого n , то ряд (1) называют рядом с положительными членами.

Теорема 2. Для сходимости числового ряда с положительными членами необходимо и

достаточно, чтобы последовательность его частичных сумм Sk была ограниченной.

	(1) сходится, то последовательность Sk сходится,
Доказательство. Если ряд an	(1) сходится, то последовательность Sk сходится,
n 1

и потому является ограниченной.	Если ряд an с положительными членами, то
	n 1

Sn 1 Sn an 1 Sn для любого n , т.е. последовательность Sk монотонно возрастает. Если Sk

ограничена, то она, как известно, имеет предел и ряд (1) сходится.

Применение этого простого (необходимого и достаточного!) условия сходимости рядов с положительными членами затруднено тем, что нахождение частичных сумм Sk не всегда возмож-

но.


Замечание. Если ряд an получен из ряда	an отбрасыванием первых N его членов, то
n N 1	n 1

его сходимость (или расходимость) от этого не изменяется. Это обусловлено тем, что критерий Коши, примененный к этим рядам, не опирается на значения первых N его членов.

Теорема 3. ( Признак сравнения 1 для рядов с положительными членами)

168


Если ряды an	(1) и bn (2) с положительными членами удовлетворяют условию:
n 1	n 1

an bn для всех n N , то из сходимости ряда (2) следует сходимость ряда (1) и из расходимости ряда (1) следует расходимость ряда (2).

Доказательство. Из сделанного замечания можно полагать, что неравенство an bn выпол-

няется для любого n . Если Sk и Sk частичные суммы рядов (1) и (2), то Sk Sk и из ограничен-

ности частичных сумм ряда (2) следует ограниченность частичных сумм ряда (1) и на основании теоремы 2 сходимость ряда (1). Если ряд (1) расходится, то Sk неограничены и Sk неограничен-

ны. Тогда на основании теоремы 2 ряд (2) расходится.

Теорема 4. (Признак сравнения 2 для рядов с положительными членами)


Если ряды an	(1) и bn (2) с положительными членами удовлетворяют условию:
n 1	n 1

lim an , то при 0 сходимость и расходимость рядов (1) и (2) одновременная. Если

n bn

0 , то из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) следует

расходимость ряда (2).

Доказательство.

Пусть

Из

определения

предела

для

/ 2 N : n N a

. Тогда на основании теоремы 3 из сходимости (1)

следует сходимость (2) и наоборот. Из расходимости (1) следует расходимость (2) и наоборот.

Пусть 0 . Тогда 0 N : n N an

bn . Из последнего неравенства утверждения тео-

ремы 4 следуют из теоремы 3.

Теорема 5. (Признак Даламбера для рядов с положительными членами).

Если общий член ряда (1) удовлетворяет условию lim

an 1

, то при 1 ряд сходится, а

n a

при 1 расходится. При 1 признак ответа не дает.

Доказательство.

Пусть

Выберем

0 столь

малым,

что 1. Тогда

N N

: n N

an 1

n 2

... n N a

Ряд

n 1

bn сходящийся (геометрическая прогрессия со знаменателем

и поэтому на основании

n N

признака сравнения сходится ряд (1). Пусть 1. Выберем 0 столь малым,

что 1.

Тогда N N

: n N

an 1

n 1

n 2

... n N a

n 1

169


Ряд bn	расходящийся (геометрическая прогрессия со знаменателем 1) и поэтому на
n N
основании признака сравнения расходится ряд (1).
Теорема 6 . (Интегральный признак Коши)
Если y f (x) монотонно убывающая на D 1; функция,			f (x) 0 и интеграл

f (x)dx сходится, то ряд an с общим членом an		f (n) сходится. Если интеграл
1	n 1

f (x)dx расходится, то и ряд расходится.

Доказательство. Из монотонности: f (n 1) f (x) f (n) для всех x n; n 1 .

n 1

Тогда	f (n 1) f (x)dx f (n) .		Если	интеграл	f (x)dx ,	то
	n				1
	m				m
0 N : n N, m n		f (x)dx f (n) f (n 1) ... f (m)			f (x)dx
	n 1				n 1

и для ряда (1) выполняется критерий Коши и ряд сходится. Если интеграл расходится, то последо-

k 1

вательность Ik f (x)dx неограниченна и частичные суммы

k 1

f (1) f (2) ... f (k) f (x)dx

f (x)dx ...

f (x)dx f (x)dx также неограни-

ченны. Последнее свидетельствует о расходимости ряда (1).

Пример 3. Исследовать на сходимость ряд

в зависимости от параметра p.

n p

Решение. Если p 0 , то ряд расходится по невыполнению необходимого признака.

Пусть p 0 . Тогда функция f (x)

монотонно убывает на 1; и интеграл

x p

x1 p

x n

. Если p 1, то интеграл сходится и

f (x)dx lim

dx lim

x 1

lim

1 p

p 1

по интегральному признаку сходится ряд. Если 0 p 1, то интеграл расходится и по интеграль-

ному признаку расходится ряд. При p 1 (гармонический ряд) расходимость ряда была доказана в примере 2.

Теорема 7. ( Радикальный признак Коши)

Пусть an ряд с положительными членами, для которого существует lim n an . Тогда

n 1

170

при 1 ряд сходится, при 1

ряд расходится. При 1 признак ответа не дает.

Доказательство. Пусть

Число 0 выберем настолько малым, что 1. Тогда

N : n N n

an n bn . Поскольку bn

сходится (геометрическая про-

n 1

грессия со знаменателем

1), по признаку сравнения

1 ряд (1) сходится. Пусть 1 .

Число

выбираем

настолько

малым,

что

Тогда

N : n N n

an n bn . Поскольку bn

расходится (геометрическая про-

n 1

грессия со знаменателем

1), по признаку сравнения 1 ряд (1) расходится.

Замечание. Для обобщенного гармонического ряда (пример 3) для любого p 0 константа

1 в

признаках

Даламбера и

радикальном

Коши. Действительно, в

признаке

Даламбера

n p

1 p

lim

lim 1

n (n 1)p

p ln n

e0 1. Однако, при p 1 ряды сходятся, а при

В признаке Коши lim n

lim e n

n p

p 1 расходятся, поэтому пограничный случай

1 может содержать сходящиеся и расходя-

щиеся ряды. Признаки Даламбера и радикальный Коши в этом случае ответа не дают.

5.3 Знакопеременные ряды.

Абсолютная и условная сходимости.

Определение. Ряд an (1)

называется абсолютно сходящимся, если сходится ряд

n 1

(2), составленный из модулей членов ряда (1).

Теорема 1. Абсолютно сходящийся ряд сходится.

Доказательство.

Если

ряд

(2)

сходится,

то

по

критерию

Коши

0 N N

: n N, m n

an 1

...

. Поскольку

an an 1

... am

an 1

...

, для ряда (1) выполняется критерий Коши и он

сходится.

Любой из достаточных признаков сходимости рядов с положительными членами может быть использован как достаточный признак абсолютной сходимости знакопеременного ряда. На-

пример, достаточный признак Даламбера абсолютной сходимости знакопеременного ряда. Если

для общего члена знакопеременного ряда an (1) выполняется условие:

n 1

171

lim an 1 1, то ряд (1) абсолютно сходится.

n an

Определение. Числовой ряд an называется условно сходящимся, если он сходится, а ряд

n 1

an , составленный из модулей его членов, расходится.

n 1

Чтобы понять разницу между абсолютной и условной сходимостями числовых рядов дока-

жем теорему, утверждающую, что члены абсолютно сходящегося ряда можно менять местами без потери сходимости и изменения суммы ряда. Условно сходящиеся ряды при изменении порядка слагаемых могут изменять свою сумму.

Теорема 2. (Дирихле, без доказательства).

Пусть ряд an (1) сходится абсолютно и m1 ,m2 ,... , mn ,... любая перестановка множест-

n 1

ва натуральных чисел. Тогда ряд bn (3) с общим членом bn amn также сходится абсолютно и

n 1

имеет ту же сумму.

Для условно сходящегося ряда справедлива теорема.

Теорема 3. (Риман, без доказательства)

	условно, то для любого числа , существует пере-
Если ряд an (1) сходится	условно, то для любого числа , существует пере-
n 1

становка членов ряда (1), при которой он сходится и имеет сумму .

Преобразования Абеля, достаточные признаки условной сходимости.

Рассмотрим преобразование конечной суммы ak bk .

k 1

Теорема 4. (Преобразование Абеля)

Для любых чисел ak и bk , к=1,2,…,m. справедливо представление:

m 1

ak bk am Bm ak Bk ,

		k 1	k 1
	ak 1 ak , Bk	b1 b2 ... bk .
где ak	ak 1 ak , Bk	b1 b2 ... bk .

Доказательство. (индукцией по числу m )

При m=2 формула справедлива : a1b1 a2b2 a2 (b1 b2 ) (a2 a1 )b1 .

Предположим, что формула верна для m и докажем ее справедливость m+1:

m 1	m	m 1
ak bk am 1bm 1 ak bk am 1bm 1 am Bm ak Bk			am 1bm 1 am Bm
k 1	k 1	k 1

172

m	m
- ak Bk + am 1 am Bm = am 1Bm 1 ak Bk .
k 1	k 1
Теорема 5. ( Признак Абеля)
		2) последовательность bn монотонна и
Ряд anbn сходится, если 1) ряд	an сходится	2) последовательность bn монотонна и
n 1	n 1

ограничена.

Доказательство. Воспользуемся преобразованием Абеля для оценки отрезка ряда:

bm an

m 1

... ak

ak bk

an 1 ... am bk 1 bk an

an 1

(1)

k n

Для любого 0

N : n N, m n

an an 1

... am

bm bn

последовательности bn :

Здесь константа

ограничивает значения модулей

членов

B для всех n .Пусть последовательность bn монотонно растет:

bk 1 bk 0( в противном случае (bk 1

bk ) 0 ).

Тогда второе слагаемое оценивается

m 1

(bk 1 bk )(an an 1 ... ak )

(bk 1 bk )

an 1 ... ak

k n

m 1

bk 1 bk

(bm

bn )

2B k n

Первое слагаемое оценивается проще:

bm (an an 1 ... am )

an an 1 ... am

Тогда

ak bk

для всех n N, m n и для ряда выполняется критерий Коши,

k n

что завершает доказательство теоремы.

Теорема 6. (Признак Дирихле)

Ряд anbn сходится, если выполняются следующие условия

n 1

1) частичные суммы Sm an ограничены

n 1

2)последовательность bn монотонно стремится к нулю.

Доказательство. Пусть для определенности bn возрастает. Воспользуемся преобразованием

Абеля. Тогда будем иметь 0 N : n N,m n

, где А – констан-

та, ограничивающая отрезки ряда

an an 1 ... ak

A, n, k . Первое слагаемое в оценивается:

173

bm (an an 1 ... am )

an an 1 ... am

Второе слагаемое с учетом знакопостоянства

bk 1 bk

0 для всех k (монотонность bn )

m 1

оценивается:

(bk 1

bk )(an

an 1 ... ak )

(bk 1 bk )

an 1

... ak

m 1

k n

A(b

)

. Тогда

для всех n N, m n и для

k 1

k n

ряда выполняется критерий Коши, что завершает доказательство теоремы.

Определение. Ряд называется знакочередующимся, если любые два соседних члена имеют


противоположные знаки : ( 1)n an	, an 0 . Следующий признак устанавливает достаточные
n 1

условия сходимости знакочередующихся рядов.

Теорема 7. ( Признак Лейбница)

Если последовательность an в знакочередующимся ряде ( 1)n an , an 0 , монотонно

n 1

стремится к нулю, то ряд сходится.

Доказательство. К знакочередующемуся ряду с монотонно убывающими an применим

признак Дирихле, поскольку все частичные суммы ряда ( 1)n ограничены.

n 1

Общая схема исследования числового ряда.

1. Проверяют выполнение необходимого признака сходимости. Если он не выполнен, ис-

следование закончено - ряд расходится.

2.Выясняют является ли данный ряд знакоопределенным. ( все члены положительные или отрицательные). Если да, то подбирают подходящий достаточный признак (сравнения с известным рядом, Даламбера, радикальный или интегральный Коши, Раабе и др.)

3.Если ряд знаконеопределен, то рассматривают ряд из модулей его членов и подбирают подходящий достаточный признак абсолютной сходимости. Если ряд из модулей сходится, то ис-

следование заканчивается – ряд сходится абсолютно.

4. Если ряд из модулей расходится, то ряд исследуется на условную сходимость. Если он знакочередующийся, то применяют признак Лейбница, если произвольный, то признак Абеля или Дирихле.

	n
Пример 1. (Ряд Лейбница) Исследовать сходимость ряда	( 1)	в зависимости от p>0.
	p
n 0	n

174

Решение. При p 1 ряд из модулей есть обобщенный гармонический ряд				1	и он схо-
			n 1 n p		и он схо-
			n 1 n p
дится, т.е. исходный ряд сходится абсолютно. При		p 0;1 абсолютной сходимости нет, хотя ряд
знакочередующийся и последовательность an	1	стремится к нулю монотонно. Тогда ряд по
знакочередующийся и последовательность an	n p	стремится к нулю монотонно. Тогда ряд по
	n p

признаку Лейбница сходится условно.

Пример 2. Пусть последовательность an стремится к нулю монотонно. Исследовать на

сходимость ряд an cos n .

n 1

Решение. Ряд знаконеопределенный, проверим выполнение условий признака Дирихле.

ei (1 ei k )

sin k

i n

Частичные суммы Sk cos n Re e

ограничены и

2sin

n 1

ряд сходится.

Лемма. Если ряды an

(1) и bn (2) с положительными членами удовлетворяют усло-

n 1

вию:

для всех n N ,

то из сходимости ряда (2) следует сходимость ряда (1). Если

an 1

bn 1

для всех n N , то из расходимости ряда (2) следует расходимость ряда (1).

bn 1

an 1

Доказательство. Если перемножить неравенства при n N, N 1,..., N m , то

aN m

bN m или bN m

aN m . Из последних двух неравенств и при-

aN m

bN m

знака сравнения 1 следует утверждения леммы.

Теорема 8. ( Признак сходимости Раабе)

Если ряд

с положительными членами и

lim n

1 p , то при p 1 ряд сходит-

n 1

an 1

ся, а при p 1 расходится.

	an
	an		p o(1)

Доказательство. Условие теоремы перепишем в виде n		1
an 1

175

(n 1)q

1 q

p 1 и

. Если bn

, то

. Пусть

an 1

bn 1

выберем число q :1 q p . Тогда ряд bn

сходится и N : n N

, что по лемме

an 1

bn 1

n 1

означает сходимость ряда (1). Пусть

p 1. Выберем число q : p q 1. Тогда ряд (2) расходится

для n N . Тогда по лемме ряд (1) расходится.

an 1

bn 1

5.4

Степенные ряды.

Определение. Степенным рядом называют функциональный ряд вида: cn x a n

(1), где

n 0

cn - его коэффициенты, a – центр ряда.

Структуру области сходимости степенного ряда подчеркивает следующая

Теорема 1.

Если степенной ряд (1) сходится в точке x x0 , то он сходится абсолютно для всех x на ин-

тервале D x :

x a

x0 a

x a

Доказательство.

сn (x a)n

cn (x0 a)n

. Поскольку ряд (1) в точке x x0 схо-

дится, его члены ограничены (даже стремятся к нулю): M :

cn (x0

a)n

M для всех n . Для каж-

x a

дого x D величина t

и ряд M t n сходящийся (ряд геометрической прогрессии).

x0 a

n 0

Тогда по признаку сравнения ряд

cn (x a)n

сходится.

n 0

Следующая теорема уточняет характер сходимости (1) на замкнутом множестве.

Теорема 2. (Абеля)

Если степенной ряд (1) сходится в точке x x0

a , то он сходится равномерно для всех x

на отрезке D x : 0 x a x0 a

a; x0 .

Доказательство. Обозначим

(x a)k

и b

Применим преобразование

(x0 a)k

k q

q 1

ak 1 bp bp 1

... bk . Из условия тео-

Абеля к сумме ck (x a)k

ak bk

aq bk

k p

176

ремы последовательность an 0

для

x D

и ak ak 1 0 . Из сходимости

(1) в точке x x0

сле-

дует, что

для

любого

0 существуют

N : p N, q p

p 1

... b

для

всех

k p .Тогда

ck (x a)k

ak 1 ak aq

(aq ap 1) aq ,

поскольку

k p

aq 1 для всех

x D . Равномерная сходимость ряда (1) на

D следует тогда из критерия Коши

равномерной сходимости.

Следствие. Пусть функция f (x)

непрерывна на отрезке D a; x0 , а при x a; x0

a n .

f (x) cn x a n . Тогда если сходится ряд сn x0 a n , то

f (x0 ) сn x0

n 0

Определение. Областью сходимости степенного ряда (1) называют множество

Dсх , со-

стоящее из тех точек x0 , в которых ряд (1) сходится. Множество Dсх

не пусто, поскольку a Dсх .

Определение. Радиусом сходимости степенного ряда называют число R sup

. Зна-

x0 Dсх

чение R соответствует тому, что Dсх = ; . Значение R 0

означает, что Dсх = a и

ряд (1) сходится только в одной точке.

Определение. Интервал a R;a R называется интервалом сходимости степенного ряда.

Следующая теорема дает возможность для вычисления радиуса сходимости степенного ря-

да.

Теорема 3. (Коши-Адамара)

. Тогда ряд(1) сходится абсолютно на интервале a R;a R

Пусть

lim n

и расхо-

дится вне отрезка a R;a R .

x a .

Доказательство.

Если lim n

то R 0 и

ряд сходится в одной точке

Ес-

R и ряд сходится на всей числовой оси. Если R 0 ,

x a

ли lim n

, то

то для

x a

lim n

1 lim n

c (x a)n

1, что

по

радикальному

признаку

Коши

означает

сходимость ряда.

Если

x a

R lim n

c (x a)n

то ряд расходится по тому же признаку.

При

x a

R признак ответа не дает : ряд (1) может как сходится, так и расходится.

Пример 1. Степенной ряд

имеет радиус сходимости R 1, сходится на интервале

n 1

1;1 , в точке x 1 расходится, а при x 1 сходится (условно).

177

	x	n	имеет радиус сходимости R 1, сходится на отрезке 1;1
Пример 2. Степенной ряд n 1
	n	2

(абсолютно).

Другую формулу для вычисления радиуса сходимости дает

Теорема 4. (Даламбера)

Пусть lim

cn 1

. Тогда

ряд (1) сходится абсолютно на интервале a R;a R и расхо-

дится вне отрезка a R;a R .

cn 1(x a)n 1

Доказательство. Если

x a

lim

n 1

lim

1, что обеспечивает

c (x a)n

(x a)n 1

сходимость ряда по признаку Даламбера. При

x a

R lim

n 1

1 и ряд расходится

c (x a)n

поскольку не выполняется необходимый признак сходимости.

Теорема 5.

Пусть степенной ряд(1) имеет радиус сходимости R 0 . Тогда для любого r : 0 r R

ряд (1) сходится равномерно на отрезке a r;a r .

Доказательство. На данном отрезке функциональный ряд (1) мажорируется числовым:

cn (x a)n

cn r n

. По определению числа R

, для R r существует x0 Dсх , для которого

x0 a

R r . Тогда по теореме 1 ряд (1)

сходится (абсолютно) для всех x :

x a

x0 a

, в

частности x a r , т.е. ряд cn r n сходится абсолютно. По теореме о мажорирующем ряде ряд

n 0

(1) сходится равномерно на отрезке a r;a r .

Отметим ряд свойств степенных рядов, основанных теоремах о равномерной сходимости.

Следствие 1. Сумма степенного ряда является непрерывной функцией на интервале сходи-

мости.

Действительно, члены степенного ряда – непрерывные функции, поэтому его сумма – не-

прерывная функция на любом отрезке a r;a r при r : 0 r R , т.е. она непрерывна на ин-

тервале a R;a R . Заметим, что непрерывность суммы на отрезке a R;a R не гарантиро-

вана.


Пример 3. Ряд xn имеет радиус сходимости R 1 и сумму (геометрическая прогрессия)
		n 0
равную S(x)	1	, не являющуюся непрерывной на отрезке 1;1 .

	1 x

178

Следствие 2. Степенной ряд (1) можно почленно дифференцировать в интервале сходимо-

сти, при этом ряд из производных также степенной имеет тот же радиус сходимости и сумму,

равную производной суммы ряда(1) внутри интервала сходимости.


	Действительно,	пусть ряд из производных	ncn (x a)n 1 (2)		имеет радиус сходимости
			n 1
R		его интервал сходимости, ряд		(1) имеет	радиус сходимости R и
R	и I2 a R ;a R	его интервал сходимости, ряд		(1) имеет	радиус сходимости R и
	a R;a R - его интервал сходимости. Пусть		~
I1			~	. Тогда ряд	~	n 1	абсолютно
I1			x I2	. Тогда ряд	ncn (x a)		абсолютно

n 1

сходится (теорема 1) и справедливо неравенство:

x a

ния это означает сходимость ряда (1) в точке

x x , т.е R R . Пусть

0 (необходимый признак), поэтому она ограничена:

cn (x

a n 1 . По признаку сравне-

~ . Последовательность x I1

0 : n	~	n 1	M .

	cn (x a)

n 1

x a

n 1

x a

n 1

Тогда для

x :

x a

справедливо неравенство: n

(x a)

. К

n 1

ряду

применим признак Даламбера , из которого следует, что он будет сходится

n 1

при

x a

Тогда по признаку сравнения ряд (2)

сходится (абсолютно) в точке x,

т.е.

x a

R R . Сравнивая два полученных неравенства, получим R R . На основании теоремы 5 ряд из производных (2) равномерно сходится на каждом отрезке a r;a r и по теореме о дифференци-

ровании функциональных рядов его сумма равна производной суммы ряда (1) на этом отрезке.

Следствие 3. Степенной ряд (1) можно почленно интегрировать на отрезке a; x и получен-

			n 1
ный ряд		cn	x a	имеет тот же интервал сходимости.
ный ряд			n 1	имеет тот же интервал сходимости.
n 0			n 1
Доказательство аналогично следствию о дифференцировании.
5.5	Ряды Тейлора.
Ряды Тейлора.
						имеет сумму f (x) в интервале a R;a R . Тогда
Пусть степенной ряд					cn x a n (1)	имеет сумму f (x) в интервале a R;a R . Тогда
					n 0
по теореме о дифференцировании степенного ряда функция							f (x) имеет производные любого по-
рядка		во		всех	точках	интервала	a R;a R ,	причем
			n(n 1) ... (n k 1) x a n k			для всех x a R;a R .
f k (x) cn			n(n 1) ... (n k 1) x a n k			для всех x a R;a R .

n k

179

Поставляя x a , получим соотношения, связывающие коэффициенты ряда (1)					со значе-
ниями производных функции		f (x) в точке x a :
f	k	(a) ck k(k 1) ... 1 ck	k! ck	f k (a)	(2)
				k!

Определение. Рядом Тейлора функции f (x) в окрестности точки x a называют степенной

ряд (1), коэффициенты которого определяются формулами (2). В частном случае, при a 0 ряд

(1) с коэффициентами (2) называют рядом Маклорена.
Таким образом, степенной ряд (1) является рядом Тейлора своей суммы. Всегда ли ряд
Тейлора функции	f (x) имеет f (x) своей суммой? Ответ в общем случае отрицательный.
			1
Пример 1.			x2	, x 0, имеет производные в точке	a 0 всех порядков,
Пример 1.	Функция f (x) e			, x 0, имеет производные в точке	a 0 всех порядков,
		0, x 0
		0, x 0

причем f k (0)

0 ,

k 0,1,...,.

2t 3

, x

Решение.

lim

0 и значение производной

(x)

0 lim f (x)

x 0

t et

x 0

доопределяется нулем. Аналогично,

выражение производной порядка k:

(x) в точке

(t)

переменной t

(x) P

где

- многочлен

степени

. Тогда

mk x

lim f k (x)

lim

P(t)

0 и поэтому f

k (0) 0 .

x 0

t et

Тогда все коэффициенты ряда Маклорена функции f (x) равны нулю и сумма ряда нулевая

для x 0 и , следовательно, не равна

f (x) .

Определение. Функция f (x)

разложима в ряд Тейлора в окрестности точки x a , если ее

ряд Тейлора сходится и имеет сумму

f (x) для x a R;a R при некотором R 0 .

Заметим, что n – ая частичная сумма ряда Тейлора совпадает с многочленом Тейлора функ-

ции

n (a)

x a

f (x) степени n: Sn (x) Tn ( f ) f (a) f (a) x a ...

Определение. Остатком ряда Тейлора называют функцию rn ( f ) f (x) Tn ( f ) . Выражение

n 1 c

n 1

остатка ряда в форме Лагранжа имеет вид: r

( f )

для c a R;a R , а в фор-

(n 1)!

ме Коши: r ( f ) 1

f n 1

(t) x t n dt .

Теорема 1. (Необходимое и достаточное условие разложимости)

Функция f (x) разложима в ряд Тейлора на множестве a R;a R тогда и только, если

180

lim rn ( f ) 0 для всех x a R;a R .

Доказательство. Следует из определения сходимости ряда.

Теорема 2. (Достаточное условие разложимости)

Если функция

f (x) бесконечно дифференцируема на

a R;a R

при

R : 0 R и

существует константа

M 0 такая, что

f n (x)

M при всех

x a R;a R

и n ,

то функция

f (x)

разложима в ряд Тейлора на a R;a R .

Доказательство.

Воспользуемся

выражением остатка ряда

форме

Лагранжа:

r ( f )

n 1

(x)

x a

n 1

MRn 1

sup

. Последовательность

бесконечно

n 1 !

n 1!

(n 1)!

x a R;a R

малая, поэтому остаток ряда стремится к нулю.

Разложение элементарных функций в ряд Маклорена.

1. Функция y e x .

Коэффициенты ряда Маклорена cn

x 0

. На любом интервале h;h производ-

ные

ex eh

ограничены,

поэтому

функция

y e x

разложима в ряд

ex 1 x

...

(3)на любом интервале h;h , т.е. на всей числовой оси.

2. Функция y chx

ex e x

Ряд для функции e x получается из ряда (3) заменой x на – x:

e x 1 x x2 ... ( 1)n xn

2! n!

Сложением рядов получим,

	chx 1		x2		x4	...	x2n	..,	x ;
	chx 1					...	2n !	..,	x ;
	2!			4!			2n !
3. Функция y shx	ex e x
		.
	2	.
	2

Поскольку shx ch x , дифференцируем ряд (4):

shx x	x3	...	x2n 1	...	x ;
			2n 1 !
3!

4. Функция y cos x .

(4)

(5)

181

cos x

;

Производные

cos x

ограничены

на

коэффициенты

cos

если n 2k 1,

. Тогда ряд для косинуса примет вид :

1 ,

если n 2k

cos x 1

... ( 1)k

x2k

...

x ;

(6)

2k !

5. Функция y sin x .

Поскольку sin x cos x , ряд для синуса получается дифференцированием ряда (6) :

sin x x

... ( 1)k

x2k 1

...

x ;

(7)

2k 1 !

6. Функция y ln(1 x) .

Ряд геометрической прогрессии

1 x x2 ... xn

...

сходится при x ( 1;1) .

1 x

Заменяя x на - x , получим

... ( 1)

... Интегрируем ряд на

1 x

ln (1 x) 1 x

отрезке 0; x :

ln(1 x) 0

x x

... ( 1)n 1

... x ( 1;1)

(8)

1 x

Поскольку функция y ln(1 x)

непрерывна на 1;1

и ряд (8) сходится в точке x 1,

(ряд Лейбница) то на основании следствия сумма ряда в точке x 1 равна ln 2 , т.е.

ln 2 1

... ( 1)n 1

...

Поэтому разложимость функции y ln(1 x)

в ряд (8)

происходит на множестве 1;1 .

7. Функция y 1 x .

Рассмотрим степенной ряд 1 x

...

1 2 ... k 1

xk ...

Найдем его радиус сходимости: ck

1 2 ... k 1

ck 1

R lim

lim

т.е. ряд сходится для x ( 1;1) и имеет там сумму S(x) . Заметим, что

k 1

1 2 ... k 1

k 1

S (x)

x ...

... и

(k 1)!

1 2 .. k 1 k

1 2 ... k 1

1 x S (x) (1

k 1!

x )

k 1

182

1 2 ... k 1

) 1 ck x

S(x) .

(k 1)!

k 1

Тогда

ln CS ln 1 x

CS 1 x .

Заметим,

что S(0) 1 C 1 и

1 x

S(x) 1 x , т.е.

1 x 1 x 1 x2 ... 1 2 ... k 1 xk ... для x ( 1;1) (9) 2! k!

5.6 Дифференциальные уравнения. Введение

Дифференциальные уравнения (ДУ) - это соотношения между независимыми переменны-

ми, искомыми функциями от этих переменных и производными или дифференциалами искомых функций.

ДУ разделяются на два класса:

а) обыкновенные дифференциальные уравнения (ОДУ)

F(x, y(x), y	(x), y 2	(x),..., y(nn ) (x)) 0,	(1)
x	x	x
б) уравнения с частными производными (УЧП)

Q(x , x ,...,x , y		, y	,..., y	, y 2	, y	,..., y(nn ) ) 0		(2)
1 2	k x1	x2	xk	x	x1x2	x	k
				1			k

Порядком ДУ называется порядок старшей производной, входящей в уравнение (1) или (2).

Проинтегрировать ДУ (1) и (2) - это значит найти соответственно такие функции y(x) и y(x1, x2 ,..., xk ) , при подстановке которых в уравнения (1) и (2) они обращаются в соответствующих областях в тождества.

Приведем примеры физических задач, приводящих к решению ДУ.

Пример 1. Согласно закону, установленному И. Ньютоном, скорость охлаждения тела про-

порциональна разности между температурой тела и температурой окружающей среды. Пусть тело нагрето до температуры T0, а температуру окружающей среды будем считать постоянной и равной

Tc<T0. Обозначим через T(t) температуру тела в момент времени t, а через K>0 коэффициент про-

порциональности, и заметим, что функция T(t) убывающая. Применяя закон Ньютона, получаем ОДУ первого порядка

Tt' (t) K(T(t) Tc ).

Полагая T(0)=T0, после интегрирования получим закон охлаждения в виде:

T (t) Tc (T0 Tc ) e Kt .

183

Пример 2. Материальная точка массы m свободно падает под действием силы тяжести

Fт=mq. Обозначим через y(t) расстояние, пройденное точкой за время t, тогда согласно второму закону Ньютона получаем ОДУ 2-го порядка

myt''2 (t) mq .

Полагая y(0) y0 , y'(0) V0 , после интегрирования получим закон движения матери-

альной точки

qt2

y(t) 2 V0t y0.

Пример 3. Рассмотрим замкнутый электрический контур, содержащий сопротивление R,

самоиндукцию L и электродвижущую силу E(t). Если через J(t) обозначить силу тока в контуре в момент времени t, то согласно 2-му закону Кирхгофа (сумма падений напряжения вдоль всякого замкнутого контура электрической цепи равна нулю) получим ОДУ первого порядка

L Jt' (t) R J(t) E(t),

определяющее закон изменения тока в данном контуре. Если предположить, что E(t) постоянна и равна E0, а J(0)=0, то закон изменения тока J(t) имеет следующий вид:

E E R t

J (t) R0 R0 e L .

Отсюда видно, что ток J(t) слагается из двух токов: тока ER0 , соответствующего закону Ома

ER t

иэкстратока замыкания R0 e L , протекающего в обратном направлении и быстро затухающего с

увеличением t.

В курсе дифференциальных уравнений рассматриваются также системы обыкновенных дифференциальных уравнений (СОДУ)

i (x, y1(x), y2 (x),..., yn (x), y1 (x),..., yn(n) ) 0,(i 1,2,...,n) ,		(3)
где yi (x),(i 1,2,...,n) искомые функции независимого переменного x.
Порядком системы (3) называется сумма порядков старших	производных функций
y1(x), y2 (x),..., yn (x).
Проинтегрировать систему (3) - это значит найти такие функции	y1(x), y2 (x),..., yn (x),	при

подстановке которых в равенства (3) последние обращаются в тождества в соответствующей об-

ласти изменения x.

5.7 ОДУ первого порядка

Полагая в (1) введения n=1, получим ОДУ первого порядка, не разрешенное относительно

производной

184

yx' f (x, y),

		F (x, y, yx' ) 0.			(1)
Если (1) однозначно разрешимо относительно yx' или x'y , то уравнения
		yx' f (x, y)			(2)
или
'			1		(3)
		xy		g(x, y)

			f (x, y)
назовём ОДУ первого порядка, разрешенными относительно производных.
Учитывая, что yx'	dy	, уравнения (2) и (3) можно записать в виде:
	dx
		dy f (x, y)dx 0 ,			(4)
		dx g(x, y)dy 0 ,			(5)
которые будем называть ОДУ первого порядка в дифференциалах.
Общий вид ОДУ первого порядка в дифференциалах будет
		M (x, y)dx N(x, y)dy 0,			(6)

где функции M(x,y) и N(x,y) определены в некоторой открытой односвязной

области D Rx2, y , причем точки, в которых одновременно обращаются в нуль функции M(x,y) и

N(x,y), называются особыми точками уравнения (6).

Рассмотрим уравнение

(2)

где функция f (x, y) определена и непрерывна в области G Rx2, y , причем областью в Rx2, y будем считать связное открытое множество, то есть: а) две любые точки этого множества G могут быть соединены ломаной, целиком принадлежащей G; б) любая точка M множества G содержится в G

вместе с некоторой окрестностью точки M.

Определение 1. Решением ОДУ (2) на промежутке a,b ПрxG называется функция

yy(x), удовлетворяющая условиям:

1)x a,b : y'(x) ;

2)x a,b : M (x, y(x)) G ;

3)x a,b : y'(x) f (x, y(x)) .

Через a,b будем обозначать связное множество на числовой оси, которое представляет

собой один из промежутков: (a,b),(a,b],[a,b),[a,b], ( ,b),( ,b],(a, ),[a, ),( , ).

185

Пример 1. Дифференциальное уравнение

yx, f (x)	(7)
имеет решениями на промежутке a,b непрерывности функции	f (x) все множество первооб-
разных
y(x) f (x)dx C,	(8)

где С - произвольная постоянная.

Из примера 1 следует, что ОДУ (2) может иметь бесчисленное множество решений, причем эта ситуация является общей. Для выделения конкретного решения необходимо задать дополни-

тельные условия, выделяющие это решение из всего множества решений. Такими условиями яв-

ляются начальные условия:

y(x0 ) y0 , M0 (x0 , y0 ) G.

(9)

Числа x0 , y0 называются начальными данными, а задача отыскания решения ОДУ (2),

удовлетворяющего начальным условиям (9), называется задачей Коши для ОДУ (2) с начальными

условиями (9).

Наряду с задачей Коши для ОДУ (2) с начальными условиями (9) рассмотрим интегральное

уравнение

			y(x) y0 f (t, y(t))dt .	(10)
			x0
Определение 2. Функция	y y(x) , определенная на промежутке			a,b , называется ре-
шением уравнения (10), если выполняются условия:
1) y y(x) - непрерывна;
2) x a,b : M (x, y(x)) G ;
		x
3) x a,b : y(x) y0			f (t, y(t))dt

		x0
Теорема 1. Функция y y(x)			является решением задачи Коши для ОДУ (2) с начальными

условиями (9) тогда и только тогда, когда она является решением интегрального уравнения (10).

Доказательство. Пусть y y(x) является решением задачи Коши для ОДУ (2) с начальны-

ми условиями (9). Тогда x a,b выполняется условие 3) определения 1, причем

x0 a,b ,y(x0 ) y0. Условия 1) и 2) определения 2 вытекают из условий 1) и 2) определения 1.

Интегрируя тождество 3) определения 1 в пределах от x0 до x a,b , получаем условие 3) оп-

ределения 2). Следовательно, y(x) является решением уравнения (10).

186

Пусть теперь y y(x)	является решением интегрального уравнения (10)	на промежутке
a,b . В силу тождества в 3)	определения 2 функция y(x) дифференцируема для x a,b и
y(x0 ) y0. Это показывает, что для функции y(x) выполнены начальные условия		(9) и условие 1)

определения 1. Условие 2) определения 1 совпадает с условием 2) определения 2. Дифференцируя по x тождество в 3) определения 2, получим тождество в 3) определения 1. Отсюда следует, что функция y(x) является решением ОДУ (2) с начальными условиями (9). Теорема доказана.

Определение 3. Будем говорить, что решение задачи Коши для ОДУ (2) с начальными ус-

ловиями (9) существует, если существует такой интервал	(x0 , x0	), 0, и существует такое
решение y(x), определенное на этом интервале и удовлетворяющее условию y(x0 ) y0.
Теорема 2. (Дж. Пеано). Если в уравнении (2)	функция	f (x, y) непрерывна в области

G Rx2, y , то решение (хотя бы одно) задачи Коши для ОДУ (2) с начальными условиями (9) суще-

ствует.

Определение 4. График решения y y(x) уравнения (2) в плоскости XOY называется ин-

тегральной кривой ОДУ (2).

Рассмотрим пространство Rx2, y и сопоставим каждой точке M0 (x0 , y0 ) из области G доста-

точно малый отрезок прямой с угловым коэффициентом tg f (x0 , y0 ), проходящей через точку

M0 . Получившееся семейство отрезков в области G назовем полем направлений, определяемым ОДУ (2). Из определения решения и интегральной кривой ОДУ (2) следует, что кривая y y(x) ,

лежащая в области G , тогда и только тогда является интегральной кривой этого уравнения, когда она гладкая и касательная в каждой её точке совпадает с направлением поля в этой точке. Отсюда получаем приближенный метод построения интегральных кривых ОДУ (2) в области G. Для удоб-

ства этого построения находят множество точек в области G с одинаковым наклоном поля.

Определение 5. Изоклиной ОДУ (2) в области G называется кривая, во всех точках которой

направление поля, определяемого ОДУ (2), одинаково.

Из этого определения следует, что множество изоклин ОДУ (2) задается уравнением

f (x, y) C,	где С принимает допустимые вещественные значения. Построив сетку изоклин, мы
можем приближенно построить интегральные кривые уравнения (2) в области G. Заметим еще,
что изоклины f (x, y) 0 и		f 1(x, y) 0 называются соответственно изоклинами нуля и бесконеч-
ности, то есть в точках первой направление поля параллельно оси OX, а в точках второй парал-
лельно оси OY.
Пример 2. Приближенно построить интегральную кривую уравнения			yx' x2	y2 , про-
ходящую	через начало	координат. Изоклинами этого уравнения	будут	окружности
		187

x2 y2	C,C 0.	Полагая	C 0,	1	,1, 3 , получим окружности с направлением поля	0,	,	, .

				3		6	4	3

Используя эту сетку изоклин строим приближенно интегральную кривую. Заметим, что решения данного уравнения в виде интегралов найти невозможно, поэтому метод изоклин наиболее целе-

сообразен.

Как видно из формулировки теоремы Пеано, она решает локальную задачу существования решения ОДУ (2), проходящего через точку M 0 G. Что же будет за пределами интервала

(x0 , x0 ) ? Для решения этого вопроса введем понятие продолжения решений ОДУ (2).

Определение 6. Будем говорить, что решение y y(x) ОДУ (2), определенное на проме-

жутке a,b ПрxG продолжимо вправо (влево), если существует решение y y1(x) этого урав-

нения, определенное на промежутке a,b1 ПрxG, b1 b ( a1,b ПрxG, a1 a ), сужение ко-

торого на a,b совпадает с y(x). Решение y y1(x) ОДУ (2) называется в этом случае продол-

жением решения y y(x) вправо (влево).

Теорема 3. Если решение y y(x) ОДУ (2) определено на промежутке a,b] [a,b , то

оно продолжимо вправо (влево).

Доказательство. Покажем продолжимость вправо. Поставим задачу Коши для ОДУ (2) с

начальными данными x0 b, y0 y(b),(b, y(b)) G. По теореме Пеано существует такой интервал

(b ,b ) ПрxG, 0, в котором существует решение y y (x), удовлетворяющее началь-

ному условию y (b) y(b). Положим

y(x),x a,b]
y1(x)			.
y		(x),x [b,b )
Легко проверить, что y y1(x) является решением ОДУ (2) на промежутке a,b ), 0,
а это означает, что решение y y(x) ,	согласно определениию 6, будет продолжимо вправо. Ана-
логично доказывается продолжимость влево. Теорема доказана.
Определение 7. Решение y y(x)			ОДУ (2) называется полным, если оно не являяется про-

должимым ни вправо, ни влево.

Из определения 7 и теоремы 3 следует, что областью определения полного решения всегда является открытый интервал ( , ) ПрxG, называемый максимальным интервалом существова-

ния решения ОДУ (2).

Обратимся опять к теореме Пеано и заметим, что она утверждает существование хотя бы одного, не обязательно единственного, решения задачи Коши для ОДУ (2) с начальными условия-

ми (9). Отсюда следует необходимость введения понятий точки и области единственности ОДУ

(2).

188

Определение 8. Точка M0 (x0 , y0 ) G называется точкой единственности ОДУ (2), если

существует такая -окрестность S(M0 , ) G этой точки, что внутри S(M0 , ) через точку M0

проходит одна и только одна интегральная кривая ОДУ (2).

Область D G , сплошь состоящую из точек единственности ОДУ (2), назовем областью единственности уравнения (2). Отсюда следует, что два любых решения ОДУ (2) из области D,

совпадающие в некоторой точке, совпадают всюду в области D.

Определение 9. Точка M0 (x0 , y0 ) называется точкой неединственности ОДУ (2), если в

любой окрестности этой точки через неё проходит более одной интегральной кривой ОДУ (2).

Определение 10. Решение y y(x) ОДУ (2) называется частным, если каждая точка, соот-

ветствующей этому решению интегральной кривой, является точкой единственности ОДУ (2).

Вся совокупность частных решений ОДУ (2) в области D называется общим решением

уравнения (2) в этой области.

Определение 11. Функция y y(x,C), где C - произвольная постоянная, называется общим

решением ОДУ (2) в области единственности D, если:

1) для любой точки M 0 (x0 , y0 ) D уравнение y0 y(x0 ,C) однозначно разрешимо относи-

тельно С, то есть C0 y 1(x0 , y0 );

2) функция y y(x,C0 ) является решением задачи Коши для ОДУ (2) с начальными дан-

ными x0 , y0.

В общем случае, интегрируя ОДУ (2) в области D G , мы получим общее решение в не-

явном виде:
	(x, y,C) 0	(11)
или
	U (x, y) C.	(12)
Определение 12. Общее решение ОДУ (2), записанное в форме (11) или (12), называется
общим интегралом, а функция U (x, y) - интегралом ОДУ (2) в области D.
Основными свойствами интеграла U (x, y) ОДУ (2) являются:
1)	интеграл U (x, y) сохраняет постоянное значение вдоль всякой интегральной кривой
y y(x)	уравнения (2), расположенной в области D;
2) для всех (x, y) D имеет место тождество
	Ux' (x, y) U y' (x, y) f (x, y) 0.	(13)

189

190


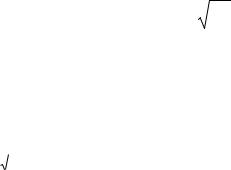
Пример 3. Для уравнения yx'		x y функция U (x, y) (x y 1) e x является интегралом,
а функция	y C ex x 1, где С	- произвольная постоянная, общим		решением в области
D Rx2, y .Самим проверить выполнимость свойств 1) и 2) интеграла U (x, y)				в данном случае.
Теорема 4 (Коши-Пикара). Если			функция f (x, y) непрерывна вместе со своей частной
производной	f y' (x, y) в области D G,		то существует, и притом единственное, решение y y(x)

задачи Коши ОДУ (2) с начальными условиями y(x0 ) y0 ,(x0 , y0 ) D , то есть существует единст-

венная интегральная кривая y y(x) уравнения (2), целиком принадлежащая области D, прохо-

дящая через точку M 0 (x0 , y0 ).

Определение 13. Решение y y(x) ОДУ (2) называется особым, если каждая точка, соот-

ветствующей этому решению интегральной кривой, является точкой неединственности ОДУ (2).

Интегральная кривая, соответствующая особому решению называется особой интегральной кри-

вой ОДУ (2).

Из определений области единственности и особого решения следует, что особые решения могут быть лишь границей области D. Из теоремы Коши-Пикара следует, что в каждой точке осо-

бой интегральной кривой нарушается хотя бы одно из условий этой теоремы.

Пример		4. Уравнение yx' 3 3 y2			имеет общее	решение y (x C)3	в областях
D (x, y)	x R,y 0 и D		(x, y)	x R,y 0 плоскости R2		. При этом функция	y 0 также яв-

1		2			x, y

ляется решением данного уравнения, однако она не получается из общего решения ни при каком значении произвольной постоянной С. Так как в точках интегральной кривой y 0 производная

'	2		не существует, то y 0 - особая интегральная кривая.
'			не существует, то y 0 - особая интегральная кривая.
f y (x, y)	3	y
Рассмотрим однопараметрическое (C - параметр) семейство
			(x, y,C) 0	(14)
гладких кривых сплошь заполняющих область D Rx2, y и предположим, что функция				диффе-
ренцируема по переменным x и y в этой области.

Поставим следующую задачу: cоставить ОДУ первого порядка в области D, для которого каждая кривая данного семейства будет интегральной кривой. Очевидно, что для решения постав-

ленной задачи достаточно исключить параметр C из системы уравнений

	'	'	'	0	(15)
x		(x, y,C) y	(x, y,C) yx	0	(15)

(x, y,C) 0

Пример 5. Пусть заданы семейства гладких кривых y C ex 0 и (y C) x C 0, где

С - параметр. Построим соответствующие ОДУ первого порядка, исключая параметр С из систем

C ex yx' 0
	y C ex 0

иy C x yx' 0 .

(y C) x C 0

Получим соответственно ОДУ yx' y и (x2 x) yx' y 0.

Определение 14. Если общие решения уравнений (2)-(6) удается найти в виде конечной

комбинации операций интегрирования, то будем говорить, что решение найдено в квадратурах.

Заметим, что в некоторых случаях левая часть уравнения
M (x, y)dx N (x, y)dy 0	(6)
является полным дифференциалом некоторой функции U (x, y), то есть
dU (x, y) M (x, y)dx N(x, y)dy.	(16)
Тогда общим интегралом ОДУ (6) будет соотношение
U (x, y) C,	(12)

где С - произвольная постоянная.

Если же при умножении обеих частей ОДУ (6) на некоторую функцию (x, y) 0 , непре-

рывную в области G непрерывности функций M (x, y) и N(x, y), левая часть полученного урав-

нения
(x, y)M (x, y)dx (x, y)N(x, y)dy 0			(17)
обращается в полный дифференциал от некоторой функции V (x, y) , то соотношение
	V (x, y) C,		(18)
где С - произвольная постоянная, является общим интегралом ОДУ (6).
Уравнения с разделяющимися переменными
Общий вид ОДУ первого порядка с разделяющимися переменными
A1(x)B1( y)dx A2 (x)B2 (y)dy 0 ,			(1)
где функции A1(x) и A2 (x) - непрерывны в промежутке x a,b ,		а функции B1( y) и	B2 ( y) -
непрерывны в промежутке y c,d .
Рассмотрим область G (x, y)	x a,b , y c, d . В этой области, кроме особых точек,

в которых одновременно обращаются в нуль функции A1(x)B1(y)		и A2 (x)B2 ( y) , уравнение (1)
имеет в общем случае два вида решений:
1) x , если a,b и A2 ( ) 0,			(2)
y , если a,b и B1( ) 0;			(3)

191

2) рассмотрим область D G , в которой A2 (x) B1( y) 0 . Уравнение (19) в области D эк-

вивалентно уравнению

A1(x)	dx	B2	( y)	dy 0 ,	(4)
A2 (x)		B1
			(y)

левая часть которого является полным дифференциалом функции

U (x, y)	A (x)		B ( y)		dy .	(5)
	1		2
	A	(x)	B	( y)
	2		1

Тогда общим интегралом ОДУ (1) в области D будет соотношение

A (x)			B (y)
1		dx	2		dy C,	(6)
A	(x)	dx	B	(y)	dy C,	(6)
2			1

где C - произвольная постоянная.

Таким образом, все множество решений ОДУ (1) состоит из решений (2), (3) и (6). Заметим,

что среди решений (2) и (3) могут быть особые, причем интегральная прямая x , a,b , бу-

дет особой интегральной прямой ОДУ (1), если A2 ( ) 0 и один из интегралов

A (x)

dx,

dx ,

(7)

(x)

где 0 достаточно мало, является

сходящимся.

Аналогично,

интегральная прямая

y , c, d ,

будет особой интегральной прямой ОДУ (1), если B1( ) 0 и один из интегра-

лов

B ( y)

B (y)

dy,

(8)

B ( y)

B (y)

является сходящимся.

Другой метод нахождения особых решений для ОДУ первого порядка, разрешенного отно-

сительно производной, связан с нарушением условий теоремы Коши-Пикара в точках исследуе-

мых решений.

Укажем ещё один способ распознавания особых решений для ОДУ (1). Если решения (2) и

(3) не получаются из (6) ни при каких частных числовых значениях С, то они являются особыми решениями ОДУ (1).

Решение задачи Коши для ОДУ (1) с начальными данными x0 , y0 (x0 , y0 ) D имеет вид:

x	A (x)		y		B ( y)
	1		dx		2		dy 0.	(9)
	A	(x)	dx		B	(y)	dy 0.	(9)
x	2		y	0	1
0				0

192

Пример 6. Всё множество решений уравнения				yx' y2 состоит из прямой y 0 и совокуп-
ности кривых y	1		, где С - произвольная постоянная. При решении вопроса будет ли инте-
		C x

гральная прямая	y 0 особой интегральной прямой обратимся к теореме Коши-Пикара. Так как
функция f (x, y) y2 и её производная f y' (x, y) 2y				непрерывны в области Rx2, y , то прямая y 0

не является особой интегральной прямой.

Пример 7. Для уравнения yx' 23 3 y , в отличие от предыдущего примера, прямая y 0 бу-

дет особой интегральной прямой. Почему?

Самостоятельно

найти

все

решения

уравнений:

dy dx 0,

yx' 1 y2 ,

yx'

yx' cos2y,

yx'

) нарисовать эскизы интеграль-

y(1 y),

ных кривых.

Уравнение

yx' f (ax by c)

(10)

линейной подстановкой z(x) ax by c приводится к уравнению с разделяющимися переменны-

ми

		zx'	b f (z) a		(11)
Однородные ОДУ первого порядка
Уравнение
		M (x, y)dx N (x, y)dy 0			(1)
называется однородным, если функции M (x, y)				и N(x, y) являются однородными функциями
по переменным	x и	y одного	и	того же порядка	k 0 , то есть
M (tx,ty) tk M (x, y),N(tx,ty) tk N(x, y).
Подстановкой	y x z(x)	уравнение (1) приводится к уравнению с разделяющимися пере-
менными
	M (1, z) z N(1, z) dx x N(1, z)dz 0 .				(2)
Функции y i	x,(x 0;i 1,2,...,k) , где i			корни уравнения
		M (1, z) z N(1, z) 0 ,			(3)

являются решениями уравнения (1), причем среди них могут содержаться особые. Особыми могут быть полуоси оси Oy : x 0( y 0). Заметим, что точка (0,0) является особой для ОДУ (1).

193

Уравнение


yx'	f	a1x b1y c1	(4)

	a2 x b2 y c2

всегда приводится к однородному уравнению или к уравнению с разделяющимися переменными,

причем:

a) если c1 c2	0, то ОДУ (4) - однородное;
б) если c1 0	или c2 0	и a1b2 a2b1 0 , то после линейной подстановки			z a1x b1 y по-
лучим уравнение с разделяющимися переменными;
в) если c1 0	или c2 0	и a1b2 a2b1 0, то система уравнений
		a x b y c 0
		1	1	1
		a2 x b2 y c2 0
имеет единственное решение (x , y ). Заменой				x u ,y v ОДУ (4) приводится к
однородному уравнению

vu' f a1u b1v .a2u b2v

Если уравнение (1) не является однородным, но после замены y zm , где m 0, обращает-

ся в уравнение

M1(x, z)dx N1(x, z)dz 0,

где функции M1(x, y) и N1(x, y) - однородные, то ОДУ (1) называется в этом случае обобщенным однородным уравнением.

Пример. Уравнение 2x2 y'x y3 xy является обобщенным однородным уравнением, так как после замены y zm оно обращается в уравнение

2mx2 zm 1z'x z3m xzm , которое при m 12 будет однородным уравнением.

Линейные ОДУ первого порядка

Общий вид линейного ОДУ первого порядка

a(x)yx' b(x)y c(x),	(1)
где функции a(x),b(x),c(x) - непрерывны на интервале (a,b) и	a(x) 0.
Разделим обе части уравнения (1) на функцию a(x) и получим эквивалентное уравнение
yx' p(x)y q(x),	(2)
где p(x),q(x) также непрерывны на (a,b).

194

Умножая обе части ОДУ (33) на функцию e p( x)dx 0, получаем ОДУ

(y e p(x)dx )'x	q(x) e p(x)dx ,	(3)
интегрируя которое получаем общий интеграл
y e p(x)dx q(x) e p(x)dxdx C		(4)
и общее решение

p( x)dx	q(x) e	p(x)dx
y e	q(x) e		dx C ,

где С - произвольная постоянная.

Разрешая ОДУ (1) относительно производной и применяя теорему Коши-Пикара что уравнение (1) не имеет особых решений.

Пример 1. Линейное уравнение

(5)

получаем,

yx' y cos x e sin x ,

после умножения обеих частей на функцию e cos xdx esin x 0, преобразуется в уравнение

( y esin x )'x 1.

Отсюда получаем общее решение ОДУ

y e sin x (x C),

где С - произвольная постоянная.

Некоторые ОДУ первого порядка становятся линейными, если x считать искомой функци-

ей, а y - аргументом, то есть

A(y) x'y B(y) x C(y),		(6)
где A( y), B( y),C( y) - непрерывные функции на интервале y (c,d).
Пример 2. Уравнение (2ey x) yx' 1, не являющееся линейным, преобразуется в линейное
x'y x 2ey ,общее решение которого имеет вид:	x ey Ce y , где С- произвольная постоянная.
Уравнение вида:
f y' (y) yx' f (y) p(x) q(x),		(7)
где p(x),q(x) - непрерывны на интервале x (a,b),	а функция f ( y) - непрерывно дифференцируе-
ма на интервале y (c, d), заменой z(x) f (y(x))	приводится к линейному ОДУ

z'x p(x) z q(x).

Одним из замечательных ОДУ вида (7) является уравнение Я.Бернулли

195

yx' p(x) y q(x) yn , (n 0,n 1), (8)

где функции p(x),q(x) - непрерывны при x (a,b). Умножая обе части этого уравнения на функ-

цию (1 n) y n ,( y 0), приходим к уравнению вида (6)

(1 n) y	n yx' p(x)(1 n)y1 n (1 n)q(x).	(9)
Полагая в (9) z(x) y1 n (x), получим	линейное уравнение

zx' (1 n) p(x)z (1 n)q(x).

Интегрируя это уравнение и возвращаясь к переменной y, получим общее решение уравне-

ния Я. Бернулли в виде

(n 1) p(x)dx

(1 n) p(x)dx

1 n

(10)

y e

C (1 n)q(x)e

где С- произвольная постоянная.

Заметим, что при n 0

функция y(x) 0 также будет решением уравнения Я.Бернулли.

Применяя к этому уравнению теорему Коши-Пикара, видим, что при n 1 решение

y(x) 0 не

является особым, а при 0 n 1 оно особое.

Пример 3. Уравнение Я. Бернулли xyx'

2y xy2 подстановкой z y 1 преобразуется в

линейное zx'

z 1, общее решение которого имеет вид

z x Cx2 . Отсюда и из подстанов-

ки получаем общее решение искомого уравнения y

, где С - произвольная постоянная.

x Cx2

Уравнение Я. Риккати

yx' p(x) y q(x) y2

r(x),

(11)

где p(x),q(x),r(x) - непрерывные в интервале

x (a,b) функции,

в общем случае не решается в

квадратурах. Однако, если известно хотя бы одно его частное решение y y1(x),

то заменой

y y1(x) z оно приводится к уравнению Я. Бернулли.

ОДУ первого порядка в полных дифференциалах

Определение 1. ОДУ первого порядка

M (x, y)dx N (x, y)dy 0 ,

(1)

где функции M (x, y), N(x, y) - непрерывны в области G Rx2, y , а левая часть есть полный диффе-

ренциал некоторой дифференцируемой функции U (x, y), назовем ОДУ в полных дифференциа-

лах. Общий интеграл этого уравнения задается соотношением

U (x, y) C.

196

M (x, y), N (x, y), M y' (x, y), Nx' (x, y) - непрерывны в области

Поставим следующие вопросы: 1. Каким образом по виду уравнения (1) можно определить,

является ли оно уравнением в полных дифференциалах? 2. Как найти функцию U (x, y) ? Ответы на эти вопросы дает следующая

Теорема 1. Уравнение (6), где

G1 G, тогда и только тогда будет ОДУ в полных дифференциалах, если для всех (x, y) G1 имеет место равенство

My' (x, y) Nx' (x, y).

(2)

Доказательство. Докажем первую часть теоремы. Пусть левая часть уравнения (1) является в области G1 G полным дифференциалом функции U (x, y), то есть имеет место тождество

M(x, y)dx N(x, y)dy Ux' (x, y)dx U y' (x, y)dy.		(3)
Из тождества (3), в силу произвольности dx и dy , получаем тождества
M (x, y) U x' (x, y),	N (x, y) U y' (x, y),	(4)
дифференцируя которые соответственно по y и по x, получим
My' (x, y) U xy'' (x, y),	Nx' (x, y) U yx'' (x, y).	(5)
В силу непрерывности функций M y' (x, y), Nx'	(x, y) в области G1 G , из теоремы о равенст-
ве смешанных производных получаем равенство (2).

Докажем вторую часть теоремы. Пусть в области G1 G выполняется равенство (2). Тре-

буется показать, что существует такая функция U (x, y), полный дифференциал которой в области

G1 тождественно равен левой части уравнения (1), то есть имеют место тождества (4). Всё множе-

ство функций, удовлетворяющих первому тождеству в (4), дается формулой
U (x, y) M (x, y)dx C( y),	(5)

где C(y)- произвольная дифференцируемая функция от y. Покажем, что C(y) можно выбрать так, чтобы выполнялось и второе тождество в (4), т.е.

U y, (x, y) N (x, y).		(6)
Подставляя (5) в (6), получим
Cy, (y) N(x, y)	M (x, y)dx ,	(7)
	y

Отсюда следует, что C( y) можно найти, если правая часть в (7) не зависит от переменной x, то есть

197

Преобразуя левую часть в (8), получим

'		' '	'		' '
'			'
Nx (x, y)			Nx
Nx (x, y)	M (x, y)dx		Nx	M(x, y)dx
		y x			x y

Nx' (x, y) My' (x, y) (по условию (2) теоремы (1)) = 0.

Таким образом, функция U (x, y), с точностью до произвольной постоянной, имеет вид
				'		(9)
U (x, y)	M (x, y)dx				dy.
		N (x, y)	M(x, y)dx
			y

Теорема доказана.

Замечание. Из доказательства второй части теоремы 1 следует практический прием реше-

ния ОДУ в полных дифференциалах.

Пример 1. Уравнение (x2 y)dx (y2 x)dy 0 является ОДУ в полных дифференциалах,

так как (x2 y)'y

( y2 x)'x

в области Rx2, y . Здесь

M (x, y) x2 y,N(x, y) y2 x. По формуле

(52) находим функцию

U (x, y)

y)dx

xy ( x)dy

C1,

где C1 -

произвольная постоянная. Таким образом, общий

интеграл искомого уравнения будет

где

C - произвольная постоянная.

Теорема 2. Решение задачи Коши для ОДУ(6) в полных дифференциалах с начальными условиями y(x0 ) y0 ,(x0 , y0 ) D G, где область D является областью непрерывности функций

M (x, y), N (x, y), M y' (x, y), Nx' (x, y) и в которой M 2 (x, y) N 2 (x, y) 0, даётся одной из формул:

x	y
M (x, y)dx N(x0 , y)dy 0,		(10)
x0	y0
x	y
M (x, y0 )dx N(x, y)dy 0,		(11)
x0	y0

причем это решение единственно.

Доказать самостоятельно, используя вторую часть доказательства теоремы 5.

198

Заметим,	что в точках, где одновременно обращаются в нуль функции M (x, y)							и N(x, y), и
называемых особыми для ОДУ (6), не гарантируется единственность решения задачи Коши.
Пример	2.	Единственным	решением	задачи	Коши	для		уравнения
(2xy 1)dx (3y2	x2 )dy 0 с начальными данными (0,0)			является функция		x	2y3		. По-

						1		1 4y4

казать самостоятельно.

Пример 3. Найти все интегральные кривые уравнения в полных дифференциалах

(x y)dx (x y)dy 0 , проходящие через точку (0,0).

Интегрирующий множитель

Рассмотрим уравнение (1)

M(x, y)dx N (x, y)dy 0 ,

снепрерывными в области D G функциями M(x, y), N (x, y), M y' (x, y), Nx' (x, y) , не являющееся

уравнением в полных дифференциалах.

Определение 1. Если при умножении обеих частей ОДУ (1) на функцию (x, y) , непре-

рывную вместе со своими частными производными и отличную от нуля в области D , уравнение

(1) обращается в ОДУ в полных дифференциалах, то есть для всех (x, y) D выполняется равен-

ство

(x, y) M(x, y) '	(x, y) N (x, y) '
y	x
или
(x, y) My' (x, y) Nx' (x, y) N (x, y) 'x (x, y) M (x, y) 'y (x, y)		(2)

то функцию (x, y) назовем интегрирующим множителем ОДУ (1), а уравнение (2) - уравнением для нахождения интегрирующего множителя.

Заметим, что решить уравнение (2) не легче, чем уравнение (1), поэтому рассмотрим слу-

чаи, когда интегрирующий множитель находится достаточно легко:

1)пусть (x, y) (x) , тогда уравнение (2) принимает вид

(x) My' (x, y) Nx' (x, y) N (x, y) 'x (x, y)

или

d (x)	My' (x, y) Nx' (x, y)	dx	(3)

	N (x, y)
(x)

Если правая часть в (3) зависит только от x, то есть

My' (x, y) Nx' (x, y)

a(x),

N (x, y)

199

то из (3) интегрированием находим (x) с точностью до постоянного множителя

		(x) C e a( x)dx ,			(4)
где C - произвольная постоянная (обычно полагают C 1).
2) пусть (x, y) ( y) , то из (2) получаем
	d (y)		M y' (x, y) Nx' (x, y)	dy	(5)
	( y)		M (x, y)	dy
	( y)		M (x, y)

Если правая часть в (5) является функцией одного только y, то есть

My' (x, y) Nx' (x, y)

b(y),

M (x, y)

то интегрируя (5) получаем

( y) C e b( y)dy ,

(6)

где C - произвольная постоянная (для удобства обычно считают C 1)

3) пусть (x, y) (x, y) , где (x, y) - известная функция, непрерывная вместе со свои-

ми частными производными в области D , тогда из (2) получаем
	d ( )	M y' (x, y) Nx' (x, y)		(7)
			d .
	( )	N (x, y) 'x M(x, y) 'y	d .
Если правая часть в (7) есть функция r( ), то

( (x, y)) C e r ( )d ,

(8)

где C - произвольная постоянная.

5.8 ОДУ первого порядка, не разрешенные относительно производной

Определение 1. Дифференциальное уравнение

F(x, y, yx' ) 0,		(1)
где функция F(x, y, yx' )- непрерывна в области V R3	' , называется ОДУ первого порядка, не
x, y, y
разрешенное относительно производной.
Определение 2. Решением ОДУ (1) в явной форме называется функция		y y(x) , опреде-
ленная на промежутке a,b р xV и удовлетворяющая условиям:
1) x a,b : yx' (x) ;

2) x a,b : (x, y(x), yx' (x)) V ;

200

3) x a,b : F (x, y(x), y'x (x)) 0 .

Определение 3. Решеним ОДУ (1) в неявной форме на промежутке a,b p xV назы-

вается решение y y(x) функционального уравнения

(x, y) 0

и обращающее ОДУ (1) в тождество для всех x a,b .

Определение 4. Решением ОДУ (1) в параметрической форме называется функция

x x(t),

y y(t),

определенная на промежутке t , и удовлетворяющая условиям

1) t , : xt' (t), yt' (t),			xt' (t) 0 ;
		y' (t )
2) t , :	(x(t), y(t),	t	) V	;
		xt' (t)

	y	'	(t )
3) t , : F (x(t), y(t),		t		) 0 .

	xt'		(t)

Определение 5. Задачей Коши для ОДУ		(1) называется задача нахождения	решения
y y(x) этого уравнения, которое удовлетворяет начальному условию
y(x0 ) y0 ,M 0 (x0 , y0 ) p ( x, y)V			(2)
Зафиксируем точку M0(x0, y0) и рассмотрим уравнение
	F (x0 , y0 , yx' ) 0		(3)
относительно yx' . Допустим, что уравнение (3) разрешимо, то есть
yx'	fk (x0 , y0 ),	(k 1,2,3,...,m).	(4)
Таким образом, в точке M0	определено m различных направлений. Все эти направления

определяют поле направлений в точке M 0.

Определение 6. Точка M 0 (x0 , y0 ) p ( x, y)V называется точкой единственности решения

задачи Коши для ОДУ (1) с начальными условиями (2), если в каждом из направлений

tg k fk (x0 , y0 ),(k 1,2,3,...,m)	(5)
через точку M0 проходит не более одной интегральной кривой уравнения (1).
Определение 7. Точка M 0 (x0 , y0 ) p ( x, y)V называется точкой	неединственности ре-

шения задачи Коши для ОДУ (1) с начальными условиями (2), если в одном из направлений (5)

через эту точку проходит более одной интегральной кривой. 201

Пусть ОДУ (1) в некоторой окрестности S(M0 , ) p ( x, y)V точки M0 (x0 , y0 )	может быть
разрешено относительно yx' , то есть распадается на m различных уравнений
yx' fk (x, y), (k 1,2,3,...,m),	(6)
разрешенных относительно производной.
Предположим, что каждое из уравнений (6) имеет общее решение
y yk (x,C),(k 1,2,3,...,m)	(7)
или общий интеграл
k (x, y) C,(k 1,2,3,...,m),	(8)

где C- произвольная постоянная.

Определение 8. Совокупность общих решений (7) или общих интегралов (8) называется общим решением или общим интегралом ОДУ (1).

Определение 9. Решение ОДУ (1) называется частным, если каждая точка соответствую-

щей интегральной кривой является точкой единственности решения задачи Коши для уравнения

(1).

Определение 10. Решение ОДУ (1) называется особым, если каждая точка соответствую-

щей интегральной кривой является точкой неединственности решения задачи Коши для уравнения

(1).

Рассмотрим вопрос о существовании особых решений у ОДУ (1). Очевидно, что особые решения ОДУ (1) могут содержать лишь те точки, в которых нарушаются условия теоремы един-

ственности. В частности, если F (x, y, yx' ) непрерывна и имеет непрерывные частные производные первого порядка, то особые решения следует искать среди множества тех точек, координаты кото-

рых одновременно удовлетворяют уравнениям

	F (x, y, p) 0,	(10)
	'	(10)
	'
	Fp (x, y, p) 0,

где p yx' . Если система (10) совместна, то исключая параметр p , получим некоторую кривую

(x, y) 0 , называемую p -дискриминантной кривой ОДУ (1). Таким образом, если ОДУ (1) имеет особые решения, то они находятся среди множества p -дискриминантных кривых уравнения (1).

Укажем первый метод метод нахождения особых решений ОДУ (1):

1)найти все p -дискриминантные кривые ОДУ (1);

2)среди найденных кривых найти интегральные кривые ОДУ (1);

3)проверить нарушение единственности в точках найденных интегральных кривых и выде-

лить среди них особые.

202

Пример 1. Рассмотрим уравнение

y xyx' eyx'				0	(11)
и составим систему уравнений (10) для определения p -дискриминантных кривых
		p	0 .

y xp e
	x e p	0
Исключая параметр p, получаем p-дискриминантную кривую
y x ln x x .					(12)
Непосредственной подстановкой убеждаемся, что (96) есть решение ОДУ (95). Общее ре-
шение уравнения (12) есть семейство прямых
	y Cx eC ,				(13)
где C - произвольная постоянная.
Значения углового коэффициента	в точках			кривых (12) и (13) соответственно	равны

y'x ln x и y'x C . Приравняем эти значения и найдем x eC . Подставим это значение x eC в

(12) и (13) и получим, что при этом значении интегральные кривые (12) и (13) соприкасаются. Та-

ким образом, через каждую точку интегральной кривой (12) в том же направлении проходит дру-

гая интегральная кривая из множества интегральных прямых (13). Отсюда и из определения осо-

бой интегральной кривой получаем, что кривая (12) - особая.
Пример 2. Для уравнения
9x 4 yx'	2	0	(14)

прямая x 0 будет единственной p -дискриминантной кривой, которая не является интегральной кривой этого уравнения. Таким образом, ОДУ (14) не имеет особых решений.

Рассмотрим простейшие случаи интегрирования ОДУ (1).

Случай 1. ОДУ (1) имеет вид

	F (yx' ) 0.		(15)
Пусть уравнение (15) имеет конечное или счетное (случай континуума мы не рассматрива-
ем) число действительных решений относительно yx' , то есть
y'	K ,	(i 1,2,3,... ) ,	(16)
x	i
где Ki ,(i 1,2,3,...) - постоянные числа. Находим общие решения уравнений (16) в виде
	y Ki x C,		(17)
где C - произвольная постоянная. Выражая из (17) постоянные Ki			и подставляя в (15), получим
общий интеграл ОДУ (15) в виде

203

y C		0 .
F

Особых решений в этом случае нет.

Пример 3. Уравнение

	yx' 4	4 yx' 2		1 0
имеет общий интеграл
y C 4		y C			2
		4			1 0.
			x
	x

Случай 2. ОДУ (1) имеет вид

			F (x, yx' ) 0 .				(18)
В этом случае могут представиться три возможности:
а) уравнение (18) разрешимо относительно yx'					, то есть
	yx'	fk (x),		(k 1,2,3,... ).			(19)
Общий интеграл каждого уравнения (19) имеет вид
			y fk (x)dx C ,
где C - произвольная постоянная. Особых решений нет.
б) уравнение (18) однозначно разрешимо относительно x , то есть
			x ( yx' ),				(20)
где (yx' ) -	непрерывно дифференцируемая функция по yx' .					Обозначим через yx'	p , тогда
уравнение (20) запишется в виде
			x ( p) .				(21)
Для	выражения искомой	функции		y	через	p воспользуемся	тождеством
dy yx' dx p dx , подставляя в которое (18), получим
	dy p 'p ( p)dp		y p 'p ( p)dp C,
где C - произвольная постоянная.
Таким образом, получили общее решение ОДУ (20) в параметрической форме
			x ( p)
			'
			'
			p p ( p)dp C
	y		p p ( p)dp C

где p - параметр, а C - произвольная постоянная. Особых решений нет.

в) уравнение (20) допускает параметрическое представление

204

x (t)	, (t , )	(22)
'		(22)
'
yx (t)

такое, что

и функции

(t)

и (t) - непрерывно дифференци-

t , :

F (t), (t)

руемы в промежутке , .

Тогда из (22) и тождества dy yx'

dx получаем dy (t) t' (t)dt . Таким образом, общее

решение ОДУ (18) в этом случае представляется в параметрическом виде

x (t)

(t) t (t)dt C

где t - параметр, а C - произвольная постоянная.

Пример 4. Уравнение

(yx' )2 x2

(23)

разрешимо относительно yx' , а именно

yx' x .

Тогда общее решение ОДУ (23) имеет вид

y x2 C, 2

где C - произвольная постоянная. Особых решений нет.

5.9 ОДУ высших порядков. Основные понятия и определения.

Определение 1. Уравнение

' ''		(n)	) 0,								(1)
F (x, y, yx , yx2	,..., yxn		) 0,
где функция F непрерывна в некоторой открытой односвязной области W Rn 2				'	,..., y			(n)		, назы-
			(x, y, y		,..., y					)
вается ОДУ n -го ( n 2 ) порядка, не разрешенным относительно старшей производной							y(nn ) .
									x
Определение 2. Уравнение
(n)	'	''	(n 1)								(2)
yxn f (x, y, yx		, yx2 ,..., yxn 1 ),
где функция f непрерывна в некоторой открытой односвязной области V Rn 1					'	,...,y			(n 1)		, на-
			(x,y	, y		,...,y					)

зывается ОДУ n-го ( n 2 ) порядка, разрешенным относительно старшей производной y(nn) . x

205

Определение 3. Решением ОДУ (2), определенным на промежутке a,b ,

функция y y(x), удовлетворяющая на этом промежутке условиям:

1) x a,b : y(x) Cna,b ;
2)	x a,b : (x, y(x), y'(x),..., y(n 1) (x)) V ;
	(n)	'	(n 1)	(x)) .
3)	x a,b : yxn	f (x, y(x), yx (x),..., yxn 1		(x)) .

Заметим, что решение ОДУ (2) может быть задано в неявной форме (x, y) 0

метрической форме x (t),y (t).

называется

(3)

или в пара-

Определение 4. График решения	y y(x)				ОДУ (2)		в плоскости R2			называется инте-
								( x, y)
гральной кривой уравнения (2).
Определение 5. Задачей Коши для ОДУ					(2) называется задача			нахождения решения
y y(x) этого уравнения, удовлетворяющего начальным условиям
y(x0 ) y0 , yx'	(x0 ) y0' ,..., y(nn 11) (x0 ) y0(n 1) ,								x0 a,b ,		(4)
						x
M (x , y , y				'	,..., y	(n 1) ) V .
0	0	0		0		0
В случае уравнения (2) второго порядка
		yx''	2 f (x, y, yx' ),								(5)
где функция f (x, y, yx' ) непрерывна в области E R3						'	, начальные условия (4) имеют вид:
					(x	,y,y	)
y(x0 ) y0 , yx' (x0 ) y0' , x0						a,b , K0 (x0 , y0, y0' ) E,					(6)

то есть при x x0 a,b задаются значения искомой функции y y(x) и её производной.

Геометрически задачу Коши для ОДУ (5) с начальными условиями (6) можно сформулиро-

вать так: на плоскости R(2x,y)

найти интегральную кривую l уравнения (5), проходящую через за-

данную

точку

K (x

, y

) Пр

в заданном

направлении

y' , причем

точка

, y) 0

K (x

, y

' ) E.

Определение

6. Если

некоторой

-окрестности

точки

S( M0 , ) R(x,y)

(x , y

) Пр

(x, y)

, y

, y'

,..., y

(n 1) ) существует только

одна

интегральная

кривая

L ( y y(x))

уравнения

(2),

проходящая

через

точку

M0 ,

причем

206

'	'	(n 1)	(n 1)		,		'	(n 1)	V ,	то	будем говорить,
y(x0 ) y0, yx (x0 ) y0 ,..., yxn 1			(x0 ) y0		,	x0 , y0 , y0 ,..., y0			V ,
что задача Коши для ОДУ (2) с начальными условиями (4) имеет единственное решение.
Теорема 1 (Коши-Пикара). Пусть функция							f в уравнении (2) непрерывна в области V V
вместе со своими частными производными				f y' , f		'	' ,..., f ' (n 1) . Тогда ОДУ (2) имеет единствен-
						y	y
ное решение y y(x)		задачи Коши с начальными условиями (4), определённое на некотором
отрезке [x0 , x0 ] Пр xV , где 0 достаточно мало.
Определение 7. Функция
				y (x,C1,C2 ,...,Cn ) ,							(7)
где C1,C2 ,...,Cn -	произвольные		вещественные				постоянные,	определённая			в промежутке

a,b Пр xV , называется общим решением ОДУ (2) в этом промежутке, если выполняются ус-

ловия:

1)x a,b : (x,C1,C2 ,...,Cn ) Cna,b ;

2)(x0 , y0, y0' ,..., y0(n 1) ) V :(система функциональных уравнений

					y0 (x0,C1,C2 ,...,Cn )
					'		'
					y0	x (x0,C1,C2 ,...,Cn )

				. .. . .. .. . .. . .. .. . .. . .. .. . .. .
				y(n 1) (x ,C ,C ,...,C )
					0				0		1		2		n
однозначно разрешима относительно C1,C2 ,...,Cn ,													то есть
				C0			1	(x	0	, y , y'				,..., y	(n 1) )
					1		1		0	0			0		0
				C0			2	(x	0	, y	0	, y'		,..., y	(n 1) )
					2		2		0		0		0		0
				.. . .. . .. . .. . .. . .. . .. . .. . . .. . .. .
					0								'		(n 1)	).
				Cn		n (x0 , y0 , y0								,..., y0		).
3) функция y (x,C0				,C0 ,...,C0 ),x a,b						является единственным решением задачи Коши для
			1	2	n
ОДУ (2) с начальными условиями (4).
Определение 8. Если общее решение (7)											ОДУ (2) задано неявно соотношением
														(x, y,C1,C2 ,...,Cn ) 0,				(8)
то равенство (8) называется общим интегралом уравнения (2).
Определение 9. Решение ОДУ (2), получаемое из (7) при конкретных числовых значени-
яхC C ,C	2	C ,...,C C , называется частным решением уравнения (2) в области D Пр															(x, y )	V .
1 1	2	2	n n														(x, y )

207

Определение 10. Решение y (x) ОДУ (2) называется особым, если через каждую точку соответствующей интегральной кривой проходят другие интегральные кривые уравнения (2).

Простейшие случаи понижения порядка ОДУ (1)-(2).

Случай 1. Уравнение (2) имеет вид:

y(nn ) f (x),					(9)
x
где функция f (x) непрерывная на промежутке x a,b . Последовательно интегрируя,					полу-
чаем общее решение уравнения (9)
y(x) ... f (x)dx...dx C1	xn 1		xn 2		(10)
		C2		... Cn 1x Cn ,
		C2		... Cn 1x Cn ,
n	(n 1)!		(n 2)!

где C1 ,C2 ,...,Cn - произвольные постоянные.

Случай 2. Уравнение (1) имеет вид:

F (x, yx(kk ) , yx(kk 11) ,..., yx(nn ) ) 0,(k 1).

Подстановка z(x) y(kk )	приводит (11) к уравнению
x
	' ''	(n k )
	F(x, z, zx , zx2	,..., zxn k		) 0
(n k) -го порядка.
Случай 3. Уравнение (1) имеет вид:
		'	''		(n)
	F (y, yx , yx2				,..., yxn	) 0.

Подстановка z(y) yx' приводит (12) к уравнению

						( y, z, z'y		, z'' 2 ,..., z(nn 1)1		)
								y	y
при этом производные				''		'''	(n) выражаются через
				yx2 ,		yx3 ,..., yxn
yx''2 yx'		'x yx'				'y yx'	z'y z
yx'''3 yx''	2	'x	yx''		2 'y yx'		zy''	2 z2	(z'y )2	z

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

z, z'y ,..., z(n 1) по формулам yn 1

y(nn) z(nn 1)1 zn 1 . . . . . . . . . . . . . . . .						(z'y )n 1 z .
x	y
Случай 4. Уравнение (1) имеет вид:
	Q' (x, y, y	'	, y	''	2	,..., y(n 1) ) 0.
	x	x		x		xn 1

(11)

(12)

(13)

208

Уравнение (13) равносильно уравнению

(n 1)

(14)

Q(x, y, yx , yx2

,..., yxn 1 ) C1

(n 1) - го порядка.

Соотношение (14) называется первым интегралом ОДУ (13).

(n)

Случай 5. Функция F в уравнении (1) однородная относительно y, yx , yx2 ,..., yxn

поряд-

ка k 0, то есть имеет место равенство

F (x,t y,t y' ,t y'' 2 ,...,t y(n) ) t k F (x, y, y' , y

''2

,..., y(n) ) .

Подстановка yx' y z, где z z(x)

новая искомая функция, приводит (1) к уравнению

(n 1)

(x, z, zx , zx2 ,..., zxn 1

) 0

(n 1) -го порядка. При этом производные y

''2 ,..., y(nn) выражаются через

,..., z

(n 1)

y, z, zx

n 1

по формулам

yx''2 yx'

'x y z 'x yx' z yzx'

y z2 zx'

yx'''3

yx''

y(z2 zx' ) 'x

y(z3

3zzx' zx''

2 )

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

y(n) y(zn . ..	.	.	. . .. .. . .. . .. .. . .. .. . .. z(n 1) ) .
xn			xn 1
Случай 6. Функция F в уравнении (1) является обобщенно однородной, то есть имеет ме-
сто равенство
F (t x,tm y,tm 1yx' ,tm 2 y	''	2	,...,tm n y(nn) ) tk F (x, y, yx'	,..., y(nn) ) .
	x		x	x

Произведём в уравнении (1) замену независимой переменной x и искомой функции

на новую независимую переменную t и новую искомую функцию z(t) по формулам

x et

y z(t) e ,

y(x)

(15)

при этом

z'emt mzemt

e(m 1)t (z'

mz)

xt'

yx' '

''2

mzt'

)e(m 1)t

(m 1)(zt'

mz)e(m 1)t

(16)

yx2

xt'

209

a0 (x)

e(m 2)t zt''2 (2m 1)zt' m(m 1)z

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Подставляя (15) и (16) в ОДУ (1), получим уравнение

(z, z	'	, z	''2	,..., z(n) ) 0,
	t		t	t n

которое подстановкой u(z) zt' приводится к уравнению

(z,u(z),uz' ,uz''2 ,...,u(nn 11) ) 0

(n 1) -го порядка.

5.10 Линейные обыкновенные дифференциальные уравнения n-го порядка (ЛОДУ)

Определение 11. ЛОДУ n-го порядка называется уравнение
	a0 (x)y(n) a1(x)y(n 1) ... an 1(x)y' an (x)y F(x),	(17)
где функции ai (x)(i 1,2,..,n)	и F(x) - непрерывны в некотором промежутке a,b ,	причем
x a,b : a0 (x) 0 .

Разделим обе части уравнения (17) на a0 (x) и обозначим pi (x) ai (x)

(i 1,2,...,n),g(x) F(x) . Получим ЛОДУ n-го порядка в канонической форме a0 (x)

y(n) p1(x) y(n 1) p2 (x)y(n 2) ... pn 1(x) y' pn (x)y g(x). (18)

Определение 12. Если g(x) 0 , то (18) называется линейным неоднородным обыкновен-

ным дифференциальным уравнением (ЛНОДУ) n-го порядка, а если g(x) 0 , то уравнение
y(n) p1(x) y(n 1) p2 (x) y(n 2) ... pn 1(x) y' pn (x)y 0	(19)

называется линейным однородным обыкновенным дифференциальным уравнением (ЛООДУ) n-

го порядка, соответствующим ЛНОДУ (18).

Замечание 1. ЛООДУ (19) на промежутке x a,b всегда имеет решение			y(x) 0 , кото-
рое называется тривиальным решением.
Запишем ЛНОДУ (18) в разрешенном относительно y(n) виде
y(n) p (x) y(n 1)	... p (x) y g(x) f (x, y, y'	, y'' ,..., y(n 1) ) .	(20)
1	n

210

	Так как	функция f в	(20)	непрерывна вместе со своими частными				производными по
y, y' ,..., y(n 1)		в области		V x a,b , y R, y' R,..., y(n 1 R ,то				в окрестности
S( , M	) V любой точки M		(x , y	0	, y	'	,..., y(n 1) ) V выполняются все условия теоремы 1 сущест-
	0	0	0	0		0	0

вования и единственности решения y y(x) задачи Коши для уравнения (20) с начальными ус-

ловиями (4). Отсюда следует, что для любого значения x0 a,b и для любых, наперед задан-

ных, вещественных значений y0 R, y0' R, y0'' R,..., y0(n 1) R существует единственное ре-

шение задачи Коши для уравнений (18) и (19) с начальными условиями (4). Таким образом, любое решение y y(x) уравнений (18) и (19) является частным и поэтому особые решения отсутствуют.

Замечание 2. Единственным решением задачи Коши для ЛООДУ (19) с начальными усло-

виями

x x0 a,b , y(x0 ) 0, y'(x0 ) 0, y''(x0 ) 0,..., y(n 1) (x0) 0

(21)

является тривиальное решение y(x) 0.

Рассмотрим линейный дифференциальный оператор n-го порядка

Ln [ ]

d n

p1 ( x )

d n 1

p2 ( x )

d n 2

... pn

1 ( x)

pn ( x )[ ] ,

(22)

dx n

dx n 1

определённый на множестве функций из класса Cna,b ,

то есть для любой функции

y(x) Cna,b на

промежутке a,b

L [ y(x)]

d n y( x)

p (x)

d n 1 y(x)

(x)

d n 2 y(x)

... p

(x) y(x) .

dxn 1

dxn 2

dxn

При этом предполагается, что все функции pi (x)(i 1,2,...,n) - непрерывны для

x a,b .

Перечислим свойства оператора Ln[] :

1) R y(x) Cna,b : Ln[ y(x)] L[ y(x)] ;

2) y1(x), y2 (x),..., yk

(x) Cna,b : Ln

yi (x) Ln[yi (x)] ;

i 1

3) 1, 2 ,..., k R y1(x), y2 (x),..., yk

(x) Cna,b : Ln

i yi (x)

i 1

i Ln[yi (x)]

i 1

Линейная зависимость и независимость функций.

Определение 13. Система функций y1(x), y2 (x),..., yn (x) , определённых на промежутке

a,b , называется линейно зависимой на этом промежутке, если

211

		n			n					. (23)
	1,	2 ,..., n R, i2	0	x a,b :	i yi (x) 0					. (23)
		i 1		i 1
Если же последнее тождество в (23) имеет место лишь в случае, когда все постоянные
i (i 1,2,...,n)	одновременно равны нулю, то система функций y (x), y						(x),..., y	n	(x)	называется
					1	2		n

линейно независимой на a,b .

Пример 1. Система функций 1, x, x2 ,..., xn является линейно независимой в любом интерва-

ле (a,b) R . В самом деле, соотношение

0 1 1 x 2 x2 ... n xn 0,

вкотором не все i R (i 0,1,2,...,n) равны нулю, не может выполняться тождественно, ибо оно

определяет собой алгебраическое уравнение n-ой степени с вещественными коэффициентами и поэтому не может иметь более чем n вещественных корней.

Пример 2. Система функций

2 x

,...,e

n x

, где все

(i 1,n) вещественные и различ-

ные, является линейно независимой в любом интервале (a,b) R . Действительно,

предположим

противное, то есть

(24)

1, 2 ,..., n R, i2

x (a,b) :

ie i x

0 .

i 1

Пусть, для определенности, n 0. Разделим обе части тождества в (24) на дифференцируем по x . Получим тождество

i ( i 1)e( i 1)x 0.

i 2

e 1x 0 и про-

(25)

Разделим обе части тождества (25) на e( 2 1) x 0 и продифференцируем по x . Получим тождество

i ( i 1)( i 2 )e( i 2 )x 0.

i 3

Рассуждая аналогично, приходим после (n 1) -го шага к тождеству

n ( n 1)( n 2 ) ( n n 1)e( n n 1 )x 0 ,

из которого, в силу различности всех i , следует n 0 , что противоречит предположению. От-

сюда следует утверждение примера 2.

Теорема 2. Если некоторая непустая подсистема y1(x),..., ym(x) системы функций

y1(x),..., yn (x) (n m) линейно зависима на промежутке a,b , то и сама система линейно за-

висима на этом промежутке.

212

Доказать самостоятельно.

Следствие. Если одна из функций системы y1(x),..., yn (x) , определённых на промежутке

a,b , тождественно равна нулю на этом промежутке, о такая система функций линейно зависи-

ма на a,b .
Определение 14. Определитель
			y1(x) y2		(x)............ yn (x)
			y1(x) y2		(x)............ yn (x)
			y' (x) y	'	(x)............ y' (x)			(26)
W[ y1(x),..., yn	(x)] W(x)		1	2		n		(26)
W[ y1(x),..., yn	(x)] W(x)		..................................
			..................................
		y	(n 1) (x)	y(n 1)		(x)... y(n 1)	(x)
		1			2	n

называется определителем Вронского для системы функций y1 (x),..., yn (x) , непрерывно дифферен-

цируемых до (n 1) -го порядка включительно на промежутке a,b .

Теорема 3. Если система функций y (x),..., y

(x) ,y (x) Cn 1

, (i 1,n)

линейно зависима на

a,b

a,b , то x a,b : W (x) 0 .

Доказательство. По условию теоремы

(27)

,...,

i i

a,b :

y (x) 0

i 1

Продифференцируем тождество в (27) по x до (n 1) -го порядка включительно. Получим

систему тождеств

1 y1(x) 2 y2 (x) ............... n yn (x) 0

1 y1' (x) 2 y2'

(x) ............... n yn'

(x) 0

(28)

...............................................................

(n 1)

(x)

(n 1)

(x) ...

(n 1)

(x) 0 .

Система (28) является

однородной

алгебраической

системой

тождеств

относительно

, 2

,..., n с определителем W (x). Так как i

0, то x a,b : W (x) 0 . Теорема

i 1

3 доказана.

Следствие. Система функций y1(x),..., yn (x) , yi (x) Cna,1b (i

) линейно незави-

1,n

сима на промежутке a,b ,

если x0

a,b : W (x0 ) 0 .

213


5.11 ЛООДУ n-го порядка с непрерывными коэффициентами.
Рассмотрим уравнение
y(n) p1(x) y(n 1) p2 (x) y(n 2) ... pn 1(x)y' pn (x) y 0,					(19)
где функции pi (x)(i		) - непрерывные в промежутке x a,b .
	1,n
Лемма 1. Если функции yi (x)(i				являются решениями уравнения (19),	то любая их
			1, m)
линейная комбинация
		y(x) 1y1(x) 2 y2 (x) ... m ym (x),			(20)

где i (i 1, m) - произвольные вещественные числа, также будет решением ЛООДУ (19).

Доказательство непосредственно следует из свойства 3 линейного дифференциального опе-

ратора n-го порядка.

Теорема 4. Если функции yi (x)(i 1,n) являются решениями ЛООДУ (19) на промежутке

a,b , то следующие утверждения эквивалентны:

1)x a,b : W[y1(x),..., yn (x)] 0 ;

2)x0 a,b : W(x0 ) 0 ;

3)система функций y1(x),..., yn (x) линейно зависима на промежутке a,b .

Доказательство. Для доказательства теоремы 4 достаточно показать, что из 1) следует 2), из

2) следует 3), из 3) следует 1).

а) соотношение 1) 2) - очевидно;

б) покажем, что 2) 3) . Рассмотрим линейную однородную алгебраическую систему

1y1(x0 ) 2 y2 (x0 ) .................

n yn (x0) 0

(x0 )

(30)

1y1(x0 ) 2 y2

n yn (x0) 0

....................................................................

(n 1)

)

(x ) 0

1 1

2 2

n уравнений

с n

неизвестными 1, 2 ,..., n R .

Так

как

определитель

этой системы

W (x0 ) 0,

то система (30)

имеет хотя бы одно ненулевое решение ( 10 , 20 ,..., n0 ), ( i0 )2 0.

i 1

Из леммы 1 и равенств (30) следует, что функция

y(x) i0 yi (x)

i 1

214

является решением ЛООДУ (19) на промежутке a,b и удовлетворяет при x x0 a,b ну-

левым начальным условиям (21). Но единственным решением ЛООДУ (19) на промежутке a,b

с начальными условиями (21), согласно замечанию 2 п.1, является тривиальное решение y(x) 0 .

Отсюда следует, что

	n	,
x a,b :	i0 yi (x) 0
i 1

где ( i0 )2 0 , то есть система функций y1(x),..., yn (x) линейно зависима на промежутке

i 1

a,b . в) соотношение 3) 1) вытекает из теоремы 3 п.2. Теорема 4 доказана.

Следствие. Если система решений y1(x),..., yn (x) ЛООДУ (19) линейно независима на

промежутке a,b , то x a,b : W (x) 0 .

Определение 15. Любая система n решений y1(x),..., yn (x) ЛООДУ (19), линейно незави-

симая на промежутке a,b , называется фундаментальной системой решений (ФСР) уравнения

(19) на этом промежутке.

Пример 3. Уравнение y'' y 0 имеет частные решения y1(x) ex и y2 (x) e x на проме-

жутке ( , ) . Так как система функций ex ,e x линейно независима (см. пример 2 п. 2) на про-

межутке ( , ) , то она представляет собой ФСР данного уравнения на этом промежутке.

Теорема 5. Для того, чтобы система n решений y1(x),..., yn (x) ЛООДУ (19) на промежут-

ке a,b являлась ФСР уравнения (19) на этом промежутке, необходимо и достаточно, чтобы

определитель Вронского W[y1(x),..., yn (x)] не равнялся нулю хотя бы в одной точке x0 a,b .

Доказательство. Необходимость следует из определения 15 и следствия из теоремы 4. Дос-

таточность следует из определения 15 и следствия из теоремы 3.

Теорема 6. ЛООДУ (19) с непрерывными на промежутке a,b коэффициентами всегда

имеет ФСР на этом промежутке.

Доказательство. Выберем произвольную числовую матрицу

	a	a	..........a
	11	12	1n
An n	a21 a22		.........a2n
An n	........................

an1 an2 .........ann

сопределителем det An n 0 и поставим для ЛООДУ (19) n задач Коши с начальными условиями:

при x x0 a,b

215

y(x0)				a11
	'	(x0 )		a21
1) y
......................
	(n 1)
			(x0 ) an1
y

	y(x0)						a12
	'	(x		)			a
2)	y		0
							22
	......................
	y(n 1) (x				0	)	a
							n2

		y(x0)				a1n
. . . . . . .			'	(x0)		a2n
	y
	n)	......................

			(n 1)
					(x0 ) ann.
	y

По теореме 1 каждая из поставленных задач имеет единственное решение на промежутке

a,b . Обозначим эти решения соответственно y1(x),..., yn (x) и составим определитель Вронско-

го для этих решений в точке x0 a,b , который совпадает с det An n 0 . Из теоремы 5 получаем,

что найденная система решений y1(x),..., yn (x) является ФСР ЛООДУ (19) на промежутке

a,b . Теорема 6 доказана.

Теорема 7. Пусть система решений y1(x),..., yn (x) ЛООДУ (19) является ФСР этого урав-

нения на промежутке a,b , тогда общее решение ЛООДУ (19) на	a,b имеет вид
y(x) C1 y1(x) C2 y2 (x) ... Cn yn (x) ,	(31)
где C1,C2 ,...,Cn - произвольные постоянные.

Доказательство. Так как любое решение ЛООДУ (19) на промежутке a,b является ча-

стным, то достаточно показать, что всякое решение													y0 (x)		задачи Коши для уравнения (19) с на-
чальными условиями x x0 a,b ,
y	0	(x ) y	0	R, y'	(x ) y	'	R,..., y(n 1)			(x	0	) y(n 1)			R
	0	0	0	0	0	0			0		0			0
задаётся формулой (31). Составим линейную алгебраическую систему
					C1y1(x0) C2 y2 (x0) .......................										Cn yn (x0 ) y0
						'			'								'	'	(32)
					C1y1		(x0) C2 y2 (x0) .......................								Cn yn			(x0 ) y0	(32)
					.............................................................................
									) C y(n 1) (x						C y(n 1)			) y(n 1) .
					C y(n 1) (x			0	) C y(n 1) (x				0	) .....	C y(n 1)	(x	0	) y(n 1) .
					1	1		0	2	2			0		n n		0	0

Поскольку определитель этой системы является определителем Вронского для функций y1(x),..., yn (x) , являющихся линейно независимыми на промежутке a,b , то он отличен от нуля в любой точке этого промежутка. Следовательно, система (32) имеет единственное решение

C10 ,C20 ,...,Cn0 . Тогда

x a,b : y	(x) C0 y (x) C0 y		(x) ... C0 y	(x) .	(33)
0	1 1	2 2	n n

Действительно, слева и справа в тождестве (33) стоят решения ЛООДУ (19), начальные ус-

ловия которых при x x0 a,b совпадают. Согласно теореме 1 о существовании и единствен-

ности решения задачи Коши для уравнения (19) с начальными условиями (32) левая и правая части в (33) совпадают на всём промежутке a,b , то есть имеет место (33). Теорема 7 доказана.

216

Следствие. ЛООДУ (19) не может содержать более чем n линейно независимых решений

на промежутке a,b .
Теорема 8. Если уравнения
		y(n) p1(x) y(n 1) ... pn 1(x) y' pn (x) y 0				(19)
		y(n) q1(x) y(n 1) ... qn 1(x) y' qn (x) y 0,				(34)
с непрерывными на промежутке a,b коэффициентами			pi (x),qi (x) (i		) ,	имеют общую
с непрерывными на промежутке a,b коэффициентами			pi (x),qi (x) (i	1,n	) ,	имеют общую
ФСР y1(x),..., yn (x) на этом промежутке, тогда
i		x a,b : pi (x) qi (x) .
i	1,n	x a,b : pi (x) qi (x) .

Доказательство. Подставляя решения yi (x)(i 1,n) из ФСР в уравнения (19) и (34) и вычи-

тая почленно полученные тождества, получим

p (x) q (x)

y(n 1)

(x) ... p

(x) q

(x)

(x) 0.

(35)

Если предположить, что x0

a,b : p1(x0 ) q(x0 ) ,

то, в силу непрерывности функций

p1(x),q1(x) ,

(a1,b1) a,b ,x0 (a1,b1) x (a1,b1) : p1(x) q1(x) .

Разделим обе части тождества (35) на

p1(x) q1(x) ,

считая

x (a1,b1).

Тогда для всех

x (a1,b1) получим тождество

y(n 1) (x)

p2 (x) q2 (x)

y(n 2) (x) ...

pn (x) qn (x)

y (x) 0 ,

p (x) q (x)

p (x) q (x) i

которое показывает, что ЛООДУ (n 1) -го порядка

y(n 1)

p2 (x) q2 (x)

y(n 2) ...

pn (x) qn (x)

y 0

p1(x) q1(x)

с непрерывными в интервале (a1,b1) коэффициентами имеет n линейно независимых на этом ин-

тервале решений yi (x)(i 1,n) , что противоречит следствию из теоремы 7. Отсюда получаем, что

a,b

: p1 (x)

q1 (x)

. Рассуждая аналогично, получим

a,b

pi (x)

(x)

. Тео-

2, n

рема 8 доказана.

Следствие. Если на промежутке a,b задана линейно независимая система n функций

y (x),..., y

(x) из класса Cn

, то можно построить ЛООДУ n -го порядка вида (19) с непрерыв-

a,b

ными на некотором интервале (a1,b1) a,b коэффициентами, для которого данная система функций будет ФСР на интервале (a1,b1) . В самом деле, так как система функций y1(x),..., yn (x)

линейно независима на промежутке a,b , то, согласно следствия из теоремы 3 п.2,

217

x0 a,b : W[y1(x0 ),..., yn (x0 )] 0 .	В силу непрерывности функции W[y1(x),..., yn (x)] на
a,b , получаем, что
(a1,b1) a,b ,x0	(a1,b1) x (a1,b1) : W[y1(x),..., yn (x)] 0 .

Предположим, что ЛООДУ n-го порядка вида (19) с требуемыми условиями построено и

y y(x) - любое его решение на интервале (a1,b1) . Тогда согласно следствия из теоремы 7 и из

теоремы 3 п.2 следует, что x (a1,b1) : W[y1(x), y2 (x),..., yn (x), y(x)] 0 , то есть

...............y1(x) y2 (x)

yn (x) y(x)

W[y (x),..., y

(x), y(x)]

y' (x) y' (x) ...............

(x) y'(x)

.........................................

y(n)

(x) y(n) (x) .....

y(n) (x) y(n) (x)

Разлагая этот определитель по элементам последнего столбца, получим уравнение

.............

y' .............

y(n)

.............

y(n 1)

..........................

............................

y(n 2) y(n 2)

... y(n 2)

y(n 1) y

... y

(n 1)

y(n)

(n)

(36)

... ( 1)n y

y2 ..........

......................

y(n)

y(n) .......

y(n)

Коэффициент при

y(n)

является определителем Вронского W[ y ,..., y

], отличным от нуля

для всех значений x a ,b

Обозначим определитель при y(n 1)

через

K(x) и разделим обе

части уравнения (36) на функцию W[y1,..., yn ] 0 . Получим ЛООДУ n -го порядка с непрерывными

на промежутке a1,b1 a,b коэффициентами, для которого система функций y1 (x),..., yn (x) яв-

ляется ФСР на a1 ,b1 .

Пример 4. Построим ЛООДУ 2-го порядка, для которого система функций 1, x2 является ФСР на соответствующем промежутке a1,b1 . Составим определитель Вронского

W[1, x2 ] 1 x2 2x 0 x 0 . 0 2x

Таким образом, в интервалах x ( ,0) и x (0, ) определитель Вронского W[1, x2 ] 0 . Со-

ставляя уравнение W[1, x2 , y(x)] 0 и производя деление обеих его частей на функцию W[1, x2 ] 2x 0,

218

получим ЛООДУ 2-го порядка y'' 1 y' 0 с непрерывными в интервалах ( ,0),(0, ) коэффи- x

циентами, для которого система функций 1, x2 будет ФСР.
Теорема 9. (Лиувилля-Остроградского) Если система решений y1(x),..., yn (x) ЛООДУ	n-го
порядка
y(n) p1(x)y(n 1) p2 (x)y(n 2) ... pn 1(x)y' pn (x)y 0	(19)

является ФСР этого уравнения на промежутке a,b , то для всех x a,b имеют место равен-

ства

W[ y (x),..., y

(x)] Ce p1 (x)dx ,

(37)

W[ y (x),..., y

(x)] W[y (x ),..., y

p1 (x)dx

(38)

(x )] e x0

где C- произвольная постоянная.

Доказательство. Так как система функций y1(x),..., yn (x) является ФСР уравнения (19) на

промежутке

a,b , то из теоремы 8

следствия

из

этой

теоремы вытекает,

что

p1(x)

K(x)

, где

W[y1(x),..., yn (x)]

y1(x)y2 (x)...............yn (x)

y, (x)y, (x)...............y, (x)

(39)

K(x)

....................................

W[y1(x),..., yn (x)]

y(n 2) (x)y(n 2) (x)...y(n 2)

(x)

y(n)

(x)y(n)

(x)............y(n)

(x)

Последнее равенство в (39) следует из формулы дифференцирования функционального оп-

ределителя. Отсюда получаем уравнение для определения W[ y1 (x),..., yn (x)]

dW[ y1(x),..., yn

(x)]

(x)dx ,

W[ y1(x),..., yn (x)]

которое после интегрирования (неопределенного или от x0

до x

из a,b ) даёт формулы (37) и

(38). Теорема 9 доказана.

Следствие. Теорема Лиувилля-Остроградского имеет непосредственное применение для

нахождения общего решения ЛООДУ 2-го порядка

y''

p1(x) y'

p2 (x) y 0

(40)

219

с непрерывными на промежутке a,b коэффициентами, если известно одно его частное реше-

ние		y y1(x) 0 на a,b . Пусть y y(x) - любое другое решение уравнения (40) такое, что
	y(x)		const	на промежутке a,b . Тогда, согласно теоремы 9, получаем

	y1(x)

W[y1(x), y(x)]

y1(x)

y(x)

C1 e

p (x)dx

' (x)

(x)

или

(x) y(x) C1

p1 (x)dx

(41)

y1(x)y

(x) y1

Разделим обе части равенства (41) на функцию y2

(x) 0 , получим

p1( x)dx

y1(x) y

(x) y1(x)y(x)

y(x)

y2 (x)

(x)

y1(x)

Отсюда получаем общее решение ЛООДУ (40) в виде:

p1 ( x)dx

y y1(x)

dx C2

(42)

2 (x)

где C1,C2 - произвольные постоянные.

Пример 5. Найдём общее решение уравнения

xy,, xy, y 0,

(43)

если известно его частное решение y x . Приведем уравнение (43)

к канонической форме

ЛООДУ 2-го порядка, разделив обе части (43) на функцию x 0

в интервалах ( ,0),(0, ) ,

y,,

y 0

(44)

и применим формулу (42),

где p1(x) 1. Получим общее решение ЛООДУ (44) в интервалах

( ,0),(0, )

y C1x

dx C2 x ,

(45)

где C1,C2 - произвольные постоянные.

5.12 ЛООДУ n-го порядка с постоянными коэффициентами.

1. Операторные многочлены и их свойства. Рассмотрим линейный диф-ференциальный

оператор Ln [] n-го порядка с постоянными вещественными коэффициентами ai (i 1, n)

[]

d n[]

d n 1[]

d n 2

[]

... a

d[]

a [] ,

(1)

dxn

1 dxn 1

2 dxn 2

n 1 dx

220

определённый на классе функций y(x) Cn

( , )

Обозначим

d 2

,...

d n

dx2

dxn

Определение 1. Выражение

M (D) Dn a1Dn 1

a2 Dn 2

... an 1D an

ak Dn k

(2)

k 0

назовём операторным многочленом, определённом на множестве функций

y(x) Cn

, то есть

( , )

для всех вещественных x справедливо тождество

Ln[ y(x)] M (D) y(x) ak Dn k y(x),(a0

1) .

k 0

Перечислим свойства операторного многочлена:

Свойство 1.

y1(x) CRn y2 (x) CRn 1, 2 C :

: M (D)( 1 y1(x) 2 y2 (x)) 1M (D)y1(x) 2M (D) y2 (x) (3)

Равенство (3) следует из свойства 3) линейного дифференциального оператора n-го поряд-

ка.

Определение 2. Определим операции сложения и умножения операторных многочленов посредством следующих равенств:

y(x) CRn : M1(D) M 2 (D) y(x) M1(D) y(x) M 2 (D)y(x) ; (4)y(x) CRn : M1(D) M2 (D) y(x) M1(D) M2 (D) y(x) . (5)

Свойство 2. Операция сложения операторных многочленов, определяемая равенством (4),

обладает свойствами коммутативности и ассоциативности.

Это свойство следует из определения 1.

Свойство 3. Операция умножения операторных многочленов, определяемая равенством

(5), обладает свойствами коммутативности и ассоциативности.

Доказательство. Покажем коммутативность операции умножения:

M	(D) M		n			m	y(x)
M	(D) M	(D) y(x)	a Dn k			b Dm i	y(x)
1	2		k			i
		k 0			i 0
	n	m		n	m
ak Dn k bi Dm i y(x)				akbi Dn m k i y(x)
k 0		i 0		k 0 i 0

221

m	n
bi Dm i ak D
i 0	k 0

Ассоциативность следует из равенств:

n k y(x) M 2 (D) M1(D) y(x) .

M 1(D) M2 (D) M3 (D) y(x) M1(D) M2 (D) M3 (D)y(x)

M1(D) M2 (D) M3 (D)y(x) M1(D) M2 (D) M3 (D) y(x) .

Свойство 4. Для операторных многочленов справедлив дистрибутивный закон:

M1(D) M 2 (D) M3 (D) y(x) M1(D) M 2 (D) M1(D) M3 (D) y(x).

Доказательство. M1(D) M 2 (D) M3 (D) y(x) M1(D) M 2 (D)

M3 (D) y(x) M1(D) M2 (D)y(x) M3 (D) y(x) M1(D) M 2 (D) y(x)

M1(D) M3 (D) y(x) M1(D) M2 (D) y(x) M1(D) M3 (D) y(x)

M1(D) M 2 (D) M1(D) M3 (D) y(x) .

Из свойств 1-4 следует, что действия над операторными многочленами подчиняются тем же законам, что и действия над обычными многочленами над полем комплексных чисел.

Составим обычный алгебраический многочлен переменной

M ( ) n a n 1	a n 2	... a	a	n	,	(6)
1	2		n 1	n

где все ai (i 1, n) - действительные числа.

Определение 3. Многочлен (6) будем называть характеристическим многочленом ЛООДУ

с постоянными коэффициентами

M (D) y Dn y a Dn 1 y a			Dn 2 y ... a				n 1	Dy a	n	y 0.	(7)
1		2					n 1		n
Пусть 1, 2 ,..., k - корни многочлена (6) кратностей				m1, m2 ,...,mk соответственно. Тогда,
согласно основной теоремы алгебры, имеем равенства
m1 m2 ... mk n ;
M ( ) ( )m1				( )m2 ( )mk .							(8)
			1	2						k
Так как действия над операторными многочленами подчиняются тем же правилам, что и
действия над обычными многочленами, то имеет место равенство
M (D) (D )m1 (D )m2 (D )mk .											(9)
1			2				k
Используя формулу (9), запишем ЛООДУ (7) в виде
M (D) y (D )m1 (D	2	)m2 (D			k	)mk		y 0 .			(10)
1	2				k

Лемма 3. Для операторных многочленов справедливы равенства:

1)M (D)e x e x M ( );

2)M (D2 )cos x M ( 2 ) cos x ;

222

3)M (D2 )sin x M ( 2 )sin x ;

4)M (D) e x y(x) e x M (D )y(x) - формула смещения.

Доказательство.

n n n

1) M (D)e x ak Dn k e x ake x n k e x ak n k e x M ( ) ;

k 0	k 0		k 0
	n	n
2) M (D2 ) cos x ak D2(n k ) cos x ak D2 D2				D2 cos x
	k 0	k 0
n
ak 2 n k cos x M ( 2 ) cos x ;
k 0
3) аналогично как и в 2);
	n	n	n k	e x (i)
4) M (D) e x y(x) ak Dn k e x y(x) ak Cni k				e x (i)
	k 0	k 0	i 0
n	n k		n

y(x) (n k i) ak Cni k e x i Dn k i y(x) e x ak (D )n k y(x) e x M (D )y(x). k 0 i 0 k 0

Пример 1. Применить формулу смещения в случае, когда операторный многочлен имеет

вид M (D) D 1 2 , а число 1.

D 1 2 ex y(x) ex D2 y(x) ex yx,,2 (x).

Вид общего решения ЛООДУ n-го порядка с постоянными коэффициентами в случае,

когда все корни характеристического уравнения простые.

Пусть все корни 1, 2,..., n характеристического уравнения

M ( ) n a n 1		a	n 2	... a			a	n	0	(11)
	1	2					n 1	n
попарно различны. Тогда функции
y (x) e 1x ,y (x) e 2 x ,..., y					n	(x) e n x				(12)
1	2				n

являются решениями ЛООДУ (7). В самом деле, подставляя функции y e k x ,(k 1, n) в уравнение

(7) и используя лемму 3, получим тождества M ( k ) 0 , что и требовалось доказать. Так как сис-

тема функций (12) с попарно различными k ,(k 1, n) линейно независима на интервале ( , ),

то она будет ФСР уравнения (7) и поэтому общее решение ЛООДУ (7) имеет вид:

n
y(x) Cie i x ,	(12)

i 1

где Ci (i 1, n) - произвольные постоянные.

Заметим, что формула (12) справедлива как в случае действительных, так и в случае ком-

плексных корней характеристического уравнения (11). Так, если имеется только одна пара ком223


плексно сопряжённых корней, например, 1 i , 2							i ,	то соответствующая система n
линейно независимых на интервале ( , ) вещественных решений ЛООДУ (7) имеет вид:
(x)	1		e 1x	1		e 2 x e x cos x ;
	2			2
1
2 (x)		1	e 1x		1	e 2 x e x sin x ;
		2			2
					3 (x) e 3 x ;			(13)

. . . . . . . . . . .

n (x) e n x .

Действительно, матрица перехода от системы (12) линейно независимых на интервале

( , ) решений ЛООДУ (7) к системе решений (13) является невырожденной и поэтому систе-

ма решений (13) также линейно независима на интервале ( , ) . Таким образом, общее реше-

ние ЛООДУ (7) в действительной форме имеет вид:

y(x) C e x cos x C		e x sin x C e 3 x ... C		e n x ,	(14)
1	2	3	n

где Ci ,(i 1,n) - произвольные постоянные.

Аналогичная ситуация возникает и в случае наличия нескольких пар комплексно сопря-

женных корней.

Вид общего решения ЛООДУ n-го порядка с постоянными коэффициентами при на-

личии кратных корней у характеристического уравнения.

Пусть характеристическое уравнение (11) имеет k различных корней i , (i 1,k) кратно-

стей mi,(i 1,k) соответственно. Тогда операторный многочлен имеет вид (10). Так как множите-

ли (D i )mi ,(i 1,k) в (10) обладают свойством коммутативности, то в случае выполнения тожде-

ства (D i )mi y(x) 0 , будет иметь место тождество

(D 1)m1 (D i 1)mi 1 (D i 1)mi 1 (D k )mk (D i )mi y(x) 0, то есть все решения каж-

дого из уравнений

(D )mi
(D )mi	y 0,(i 1, k)			(15)
i
являются решениями ЛООДУ (7).
Аналогично, в силу коммутативности операторов (D i ) в (15), имеем
(D )mi 1 (D ) y 0,
i	i
то есть решения уравнений
(D i ) y 0,(i			)	(16)
(D i ) y 0,(i		1, k	)	(16)

224

являются решениями уравнений (15). Но каждое уравнение (16) имеет решение y(x) e i x . Пока-

жем, что функции y(x) xse i x ,(s 0,1,2,...,mi 1) являются решениями уравнений (15). В самом деле, подставим эти функции в (15) и получим тождества

(D i )mi (xse i x ) e i x Dmi xs 0.

Таким образом, каждому корню i (i 1,k)		кратности mi	соответствует mi		решений
y (x) e i x ,y	2	(x) xe i x ,..., y	m	(x) xmi 1e i x	(17)
1	2		m
			i

уравнения (7). Система n решений (7), где i 1,k , линейно независима на интервале ( , ) по теореме 14 о квазиполиномах и поэтому будет ФСР ЛООДУ (7) на этом интервале. Отсюда полу-

чаем общее решение ЛООДУ (7) в случае наличия кратных корней у характеристического уравне-

ния (11)

k
y(x) Pms 1(x)e s x ,	(18)
s 1

где полиномы Pms 1(x) имеют произвольные коэффициенты.

Заметим, что если среди корней характеристического уравнения (11) есть кратные ком-

плексные корни, то при необходимости получения фундаментальной системы действительных решений для ЛООДУ (7) поступают также, как и в случае простых комплексных корней, а именно:

пусть числа 1	i , 2	i - корни кратности m1		m2	m , тогда 2m комплекснозначным
линейно независимым на интервале ( , )			решениям	y(x) xse i x ,(s 0,1,2,...,m 1;i 1,2) соот-
ветствуют	2m	действительных	линейно		независимых	решения

xse x cos x,xse x sin x,(s 0,1,2,...,m 1) . Отсюда следует, что если характеристическое уравнение

(11) имеет

p пар

комплексно

сопряженных корней

i(1) i i i , i(2)

i i i

кратностей

mi (i

)

и q действительных корней s (s

) кратностей mp s , то общее решение ЛООДУ

1, p

1,q

(7) в действительной форме имеет вид:

(1)

(2)

(3)

y(x) e i

Pmi 1(x)cos i x Pmi 1(x)sin i x e s

Pmp s 1(x) , (19)

i 1

s 1

где полиномы P(1)

(x),P(2)

(x),P(3)

(x)

) - имеют произвольные коэффициенты.

1, p

1, q

m 1

p s

Пример 2. Найдём общее решение ЛООДУ

M (D) y D(D 2)3 (D2 4)2 y 0.

Корнями соответствующего характеристического уравнения

M ( ) ( 2)3 ( 2 4)2 0

225

будут	числа	1 0, 2 2, 3 2i, 4 2i ,						кратности которых				соответственно равны
m1 1,m2	3,m3	2,m4 2. Согласно формуле (19), общее решение данного уравнения имеет вид:
		y(x) C (C	2	C	x C	4	x2 )e2x (C		5	C x) cos2x (C	7	C x)sin 2x ,
		1	2	3		4			5	6	7	8

где Ci,(i 1,8) - произвольные постоянные.

5.13 ЛНОДУ n-го порядка с постоянными коэффициентами.

Линейные неоднородные уравнения с постоянными коэффициентами n-го порядка.

Пусть дано дифференциальное уравнение:

a y n	a y n 1	a	n	y f x ,	(1)
0	1		n

с постоянными коэффициентами a0 ,a1, ,an ,a0 0.

Теорема. Общее решение неоднородного уравнения (1) равно сумме общего решения со-

ответствующего однородного уравнения и какого-либо частного решения неоднородного уравне-

ния.

Отыскание общего решения соответствующего однородного уравнения осуществляется по правилам, изложенным в предыдущем разделе. Частное решение неоднородного уравнения для случая правых частей специального вида находится методом подбора, или иначе, методом неопре-

деленных коэффициентов.

Общий вид правой части уравнения (1), при котором применим метод неопределенных ко-

эффициентов, следующий:

	f x e x P x cos x Q x sin x .				(2)
			l	m
Здесь Pl x и Qm x - многочлены степени l и m соответственно.
В этом случае частное решение уравнения (1) ищем в следующем виде:
	y	ч. н	xs e x P	x cos x Q x sin x ,	(3)
		ч. н	k	k
где k max l,m ,	Pk x и Qk x - многочлены от			x степени k общего вида с неопределенными
коэффициентами, а s - кратность корня i				характеристического уравнения. (Если i
не является корнем, то s 0 .) Разберем его решение на примерах.
Пример 1.	y 2y 3y 4e x .
Решение. Сначала найдем общее решение соответствующего однородного уравнения
			y 2y 3y 0.

Его характеристическое уравнение:

2 2 3 0

или 1 3 0

226

имеет корни 1 1 и 2 3.

Общее решение однородного уравнения:

yo.o C1 ex C2 e 3x .

Теперь нужно найти частное решение неоднородного уравнения. Сравнивая его правую часть с формулой (3), видим, что 1, 0. Число i 1 корнем характеристического уравнения не является, следовательно, s 0 . P и Q - многочлены нулевой степени, следовательно,

частное решение будем искать в виде

yч.н A e x .

Удобно расположить y, y , y в столбик, написав слева значения коэффициентов из исход-

ного уравнения:

3 yч.н Ae x ; 2 yч.н Ae x ; 1 yч.н Ae x .

Сложив всё, получим:

e x 3A 2A A 4e x ,

4A 4, A 1,

yч.н e x ,

а общее решение неоднородного уравнения

yо.н C1 ex C2 e 3x e x .

Пример 2.

y 4y 3sin 2x.

Решение. Однородное уравнение имеет вид

y 4y 0,

его характеристическое уравнение:

2 4 0, корни 1,2 2i .

Общее решение

yo.o C1 cos2x C2 sin 2x.

Чтобы правильно выбрать вид частного решения неоднородного уравнения согласно фор-

муле (3), сравним правую часть уравнения с общим её представлением по формуле (2). Очевидно,

i 2i является однократным корнем характеристического уравнения, поэтому s 1.

В физике это явление называется резонансом, суть его в совпадении собственной частоты колеблющейся системы и частоты приложенной внешней силы.

Кроме того, замечаем, что степени многочленов P и Q - нулевые. Вид частного решения:

227

yч. н x Acos2x B sin 2x .

Подставим в исходное уравнение:

4	yч. н x Acos2x Bsin 2x ;

0yч.н Acos2x Bsin 2x x2Asin 2x x2b cos2x ;

1yч. н 2 2Asin 2x 2B cos2x x 4Acos2x 4Bsin 2x .

Витоге

4Asin 2x 4B sin 2x 3sin 2x ;

4A 3,

B 0 ,

ч.н

x cos2x .

Общее решение:

C cos2x C

sin 2x

x cos2x .

о.н

Пример 3.

f x ,

где f x равна:

1) 10e x , 2) 3e2x , 3) 2sin x , 4)

2x2 30 ,

5) 2e x cos

, 6) x 1 e 2x .

1. y 3y 2y 10e x .

Решение. Xарактеристическое уравнение

2 3 2 0 ,

корни его

2. Общее

решение однородного уравнения:

о.о

C ex C

e2x .

Частное решение неоднородного уравнения ищем в виде

yч.н Ae x ,

так как из сопостав-

ления правой части уравнения с формулой (2) очевидно, что 1 не является корнем характе-

ристического уравнения, т.е. резонанса нет.

Подставив yч.н в исходное уравнение, получим
Ae x Ae x 2Ae x			10e x ,
откуда
6A 10 ,	A	5	.
6A 10 ,	A		.
	3

Общее решение неоднородного уравнения:

yо.н C1 ex C2 e2x 5 e x . 3

2. y 3y 2y 3 e2x .

228

Решение. Правая часть уравнения имеет вид Ae2x ,		2 совпадает с корнем характери-
стического	уравнения, s 1, поэтому вид частного	решения неоднородного уравнения
yч.н Axe2x .	Найдем А:

2y Ax e2x ;

3 y 2Ax A e2x ;

1y 2A 4Ax 2A e2x .

После сложения получим
e2x x 2A 6A 4A 3A 4A 3 e2x , Ae2x 3e2x ,					A 3 .
Общее решение неоднородного уравнения:
y	ч.н	C ex C	2	e2x 3x e2x .
	ч.н	1	2
3. y 3y 2y 2sin x .
Решение. Правая часть уравнения имеет вид			e x sin x, 0, 1.		Корни характеристи-

ческого уравнения не совпадают с числом i i , следовательно резонанса нет и частное ре-

шение имеет вид:

yч. н Acos x Bsin x .

Подставив в уравнение, получим

Acos x B sin x 3 Asin x B cos x 2 Acos x Bsin x 2sin x .

Приравняв коэффициенты при		sin x		и cos x в левой и правой частях равенства, имеем:
A 3B 0;					откуда A					3	,	B		1	.


3A B 2,							5					5
В итоге общее решение уравнения:
y			C ex C				e2x	3	cos x			1	sin x.
	о.н					2
				1			5					5

4. y 3y 2y 2x3 30 .

Решение. Частное решение ищем в виде многочлена с неопределенными коэффициентами,

степень которого совпадает со степенью многочлена в правой части уравнения: yч.н Ax3 Bx2 Cx D .

После подстановки в уравнение получаем

6Ax 2B 3 3Ax2 2Bx C 2 Ax3 Bx2 Cx D 3x3 30 .

Приравняв коэффициенты при x3, x2 , x и 1 слева и справа, имеем:

229

						2A 2 ,
				9A 2B 0 ,
				9A 2B 0 ,
				6A 6B 2C 0 ,
				6A 6B 2C 0 ,

			2B 3C 2D 30 .
Откуда
	A 1 ,		B		9	,	C	21		,		D			15	.
	A 1 ,		B			,	C			,		D				.
				2			2					4
Общее решение уравнения
y		C ex		C e2x x3					9		x2		21	x			15	.
y	о.н.	C ex		C e2x x3							x2			x				.
	о.н.	1		2			2					2					4
							2					2					4

5. y 3y 2y 2 ex cos x . 2

Решение. Частное решение ищем в виде:

yч. н

Acos

Bsin

После подстановки в уравнение получаем:

, B

Общее решение:

yо.н C1 e

cos

2sin

. 2

Теорема (принцип суперпозиции или наложения). Если yi x являются решениями

уравнений

a x y n a x y n 1 a

x y f

x ,

i 1, 2, , k ,

то функция

y x y1 x y2 x yk x

является частным решением уравнения

a x y

n a

x y n 1 a

x y f

x f

6. y 3y 2y x 1 e 2x .

Правую часть уравнения представим в виде суммы

f1 x = x + 1 и f2 x e 2x

и найдем частные решения y1

и y2

уравнений

y 3y 2y x 1 и y 3y 2y e 2x .

Методом неопределенных коэффициентов легко получить:

230

y	1	x	5	,	y			1	e 2x .
1	2	4				2	12
	2	4					12

В соответствии с принципом суперпозиции полагаем, что частное решение уравнения

yч.н y1 y2. Тогда общее решение исходного уравнения:

y		C ex C		e2x	1	x	5		1	e 2x .
	о.н		2
		1		2		4		12

5.14 Вопросы к экзамену по курсу «Ряды и ОДУ»

1.Понятие числового ряда. Сходящийся ряд, его сумма. Критерий Коши сходимости числового ряда. Необходимое условие сходимости ряда. Основные свойства сходящихся рядов.

2.Ряды с неотрицательными членами. Признаки сравнения.

3.Признаки Даламбера и Коши. Интегральный признак Коши-Маклорена. 4.Абсолютная и условная сходимость. Признак Лейбница.

5.Признаки сходимости Абеля и Дирихле.

6.Понятие степенного ряда. Теорема Абеля.

7.Радиус сходимости и область сходимости степенного ряда.

8.Промежутки равномерной сходимости степенного ряда. Непрерывность суммы степенного ряда. 9.Теоремы о почленном интегрировании и дифференцировании степенного ряда.

10.Разложение функций в степенные ряды. Разложение некоторых элементарных функций в ряд Тейлора.

11.ОДУ первого порядка, разрешенные относительно производной. Определение решения. По-

становка задачи Коши.

12.ОДУ первого порядка, разрешенные относительно производной. Понятие поля направлений.

Изоклины. Определение интегральной кривой. Определение существования задачи Коши. Тео-

рема Пеано (формулировка). Единственность решения задачи Коши. Теорема Коши-Пикара

(формулировка).

13.ОДУ первого порядка, разрешенные относительно производной. Определение точки единст-

венности и неединственности решения задачи Коши. Область единственности. Определение ча-

стного и особого решений. Где могут располагаться особые решения?

14.ОДУ первого порядка, разрешенные относительно производной. Определение продолжения решения вправо (влево). Теорема о продолжимости.

15.ОДУ с разделяющимися переменными и приводимые к ним линейной заменой. Метод нахож-

дения общего и особых решений.

231

16.Однородные ОДУ и приводимые к ним переносом начала координат. Метод нахождения обще-

го и особых решений. Обобщенные однородные ОДУ.

17.Линейные ОДУ с непрерывными на интервале(a,b) коэффициентами. Нахождение области единственности и общего решения. Выяснить возможность существования особых решений.

Уравнения Бернулли и Риккати. Метод нахождения общего и особых решений.

18.ОДУ в полных дифференциалах.

19.Понятие интегрирующего множителя. Уравнение интегрирующего множителя. Нахождение

интегрирующего множителя в простейших случаях.

20.ОДУ высших порядков, разрешенные относительно старшей производной. Определение реше-

ния. Задача Коши и определение общего решения.

21.ЛОДУ n-го порядка с непрерывными на интервале (a,b) коэффициентами. Определение ре-

шения. Постановка задачи Коши и теорема Коши-Пикара для таких уравнений. Выяснить воз-

можность существования особых решений.

22.Определения линейной зависимости и линейной независимости системы функций, определен-

ных на интервале (a,b). Доказать, что системы функций 1, x, x2 ,...,xn (n N) и

e 1x ,e 2 x ,...,e n x ( i j для i j , где i, j 1,2,...,n	и все i R) линейно независимы на беско-
нечном интервале ( , ).

23.Понятие определителя Вронского для системы функций y1(x), y2 (x),..., yn (x) . Теорема о необ-

ходимом условии линейной зависимости системы функций y1(x), y2 (x),..., yn (x) .

24.ЛООДУ n-го порядка с непрерывными на интервале (a,b) коэффициентами. Теорема о линей-

ной комбинации решений.

25.Определение фундаментальной системы решений (ФСР) ЛООДУ n-го порядка. Теорема о существовании ФСР у ЛООДУ n-го порядка с непрерывными на интервале (a,b) коэффици-

ентами. Теорема о структуре общего решения ЛООДУ n-го порядка с непрерывными на ин-

тервале (a,b) коэффициентами.

26.Теорема Лиувилля-Остроградского и ее применение для нахождения общего решения ЛООДУ второго порядка, если известно одно нетривиальное частное решение этого уравнения.

27.ЛНОДУ n-го порядка с непрерывными на интервале (a,b) коэффициентами и правой частью.

Теорема о структуре общего решения. Принцип суперпозиции.

28.Понятие операторного многочлена. Основные операции и свойства. Характеристический мно-

гочлен и характеристическое уравнение ЛООДУ n-го порядка с постоянными коэффициен-

тами. Действие операторного многочлена на простейшие функции: e x , cos x , sin x , e x y(x).

232

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
29.03.2016284.41 Кб2103 АЛГЕБРА_ovs_2-8.pdf
#
13.11.20183.16 Mб21031093_B6EB8_kontamin_f_voyna_v_srednie_veka.doc
#
28.03.2016432.64 Кб24032700,62 ФОНЕТИКА.doc
#
04.12.2018292.35 Кб904 КРдля тетрадей.doc
#
28.03.2016170.5 Кб13040400_62_b_socrab.doc
#
29.03.2016594.66 Кб1605-06 МАТАН.pdf
#
17.04.2019813.06 Кб5065420_F215F_lekcii_po_mikroekonomike.doc
#
17.04.2019675.84 Кб7074835_30227_shpargalki_mikroekonomika_vstupite....doc
#
22.11.2018280.06 Кб4080825 КОМИ-ПЕРМЯКИ СЕГОДНЯ.doc
#
28.03.2016471.04 Кб221 УМК по Бюджетной системе 2008.doc
#
06.09.2019244.74 Кб101 St_math.doc