Кочнева Л.Ф., Хаханян В.Х. ИССЛЕДОВАНИЕ ОПЕРАЦИЙ

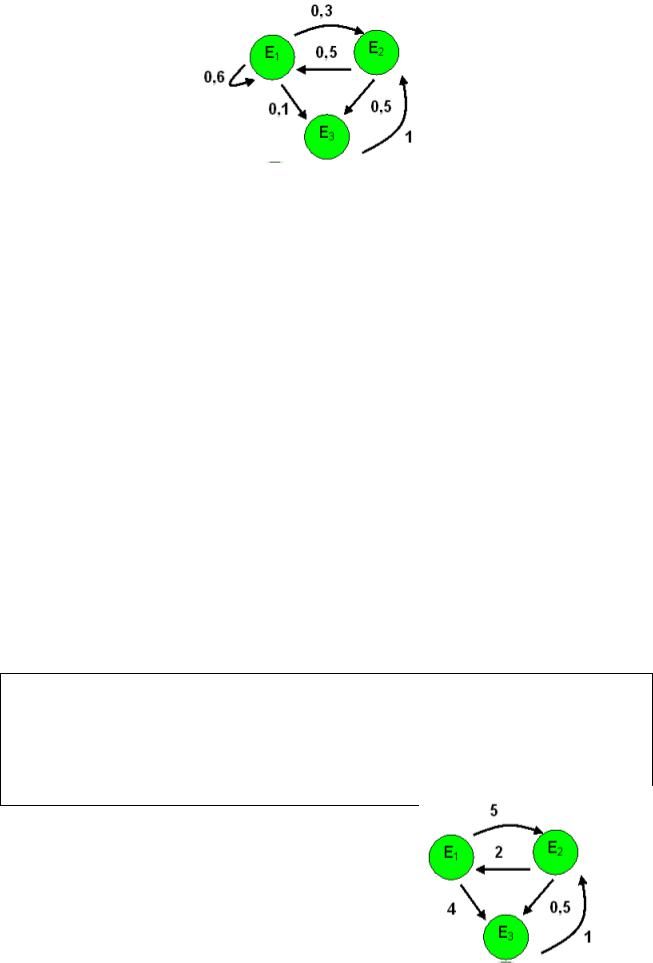
Выпишите систему уравнений для нахождения q*.

Ответ: Василий спит в среднем 10 часов 26 минут в день

7.2 Марковские цепи с конечным множеством состояний и непрерывным временем

Основные понятия Если система может переходить в другое состояние случайным образом в произвольный

момент времени, то говорят о случайном процессе с непрерывным временем. В отсутствии последействия такой процесс называется непрерывной марковской цепью c непрерывным временем.

Описание марковской цепи с непрерывным временем:

Цепь в каждый момент времени может находиться только в одном из состояний

E1,E2,…,En.

Переходы из одного состояния в другое могут происходить в произвольные моменты времени t.

Если система в момент времени t0 находится в состоянии Ei, то вероятность оказаться в состоянии Ej в момент времени t0+t не зависит от t0 и равна pij(t).

Функция pij(t) дифференцируема при t=0: pij/(0)=aij.

Числа aij при i≠j называются интенсивностями перехода из Ei

в Ej

На графе состояний системы численные значения aij ставят рядом со стрелками, показывающими переходы в вершины графа.

130

Свойства матрицы интенсивностей:

1) ∑ pij = 1 ∑aij = 0

j j

2)aij ≥ 0 при i ≠ j

3)aii ≤ 0

Число bi= – aii называется интенсивностью выхода из Ei

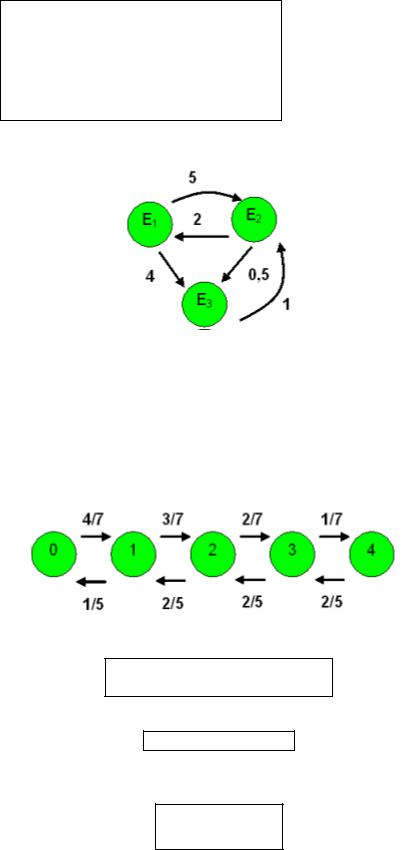
Задача. Выписать матрицу интенсивностей для марковской цепи. (Петли не рисуются!)

Задача. Имеется 4 локомотива и 2 ремонтные бригады. Интенсивность поломок каждого локомотива примерно 1 раз в неделю. В случае поломки локомотив ремонтируется одной бригадой. Среднее время ремонта 5 дней. Нарисовать граф для этой марковской цепи.

Ответ.

Уравнения Колмогорова Вектор вероятностей состояний

q = (q1, q2 , ..., qn )

Свойство вектора вероятностей состояний:

Сумма всех qj равна 1

Теорема. Вектор вероятностей состояний q=q(t) удовлетворяет система уравнений Колмогорова

q′ = q A

131

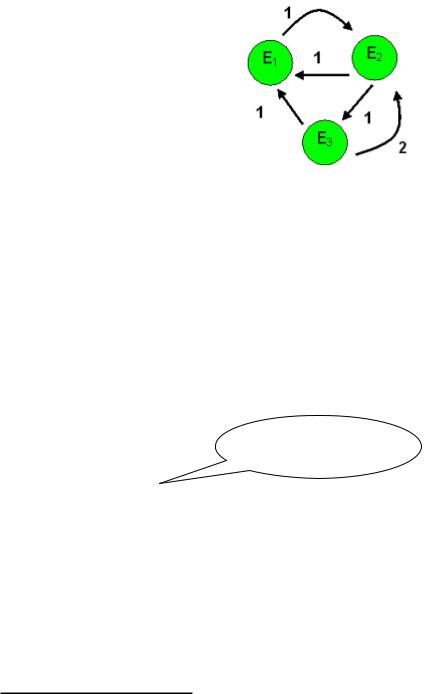
Задача. Сейчас система находится в E1 или E2 с равной вероятностью. Найти самое вероятное состояние в момент времени t=10.

Решение. q(0)=(0,5; 0,5; 0), q(10)=?

И ещё начальное условие

q1 (0) = 0,5

q2 (0) = 0,5

q3 (0) = 0

Далее решаем систему уравнений.

1)Одно из уравнений (кроме последнего) выбрасываем.

2) Из последнего уравнения выражаем “выброшенное” q и подставляем в остальные

3)Если в каком-то уравнении осталась одна неизвестная, решаем его. Если нет, то выражаем из одного уравнения неизвестную и подставляем в другое.

132

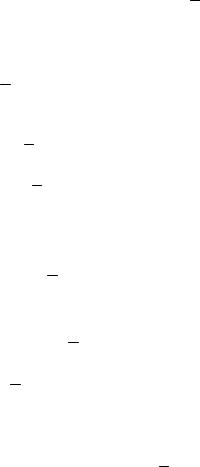
y′ = 1− 2 y y′ + 2 y = 1

1) λ + 2 = 0 λ = −2 y00 = Ce−2t

2) yчаст = A A′ + 2A = 1 A = 1 2

4) Подставляем в оставшееся уравнение

q3′ = 1− 1 − 4q3

2

y′ + 4 y = 1 2

1) y′ + 4 y = 0

λ+ 4 = 0 λ = −4 y00 = C1e−4t

2)y′ + 4 y = 1

2

yчаст = A1

(A1 )′ + 4(A1 ) = 1

2

4 A1 = 1 ...

2

q3 = y = yчаст + yoo = C1e−4t + 1 8

q1 (0) = 0,5

( ) =

q2 0 0,5

q3 (0) = 0

Ответ: При t=10 наиболее вероятное состояние – E1 Эргодические цепи Понятие эргодичности

Наибольший интерес обычно представляет поведение марковской цепи за большой период времени Марковская цепь с непрерывным временем называется эргодической (или регулярной), если:

Для любого начального вектора q(0) существует предел

Это предел не зависит от q(0). Признак эргодичности

133

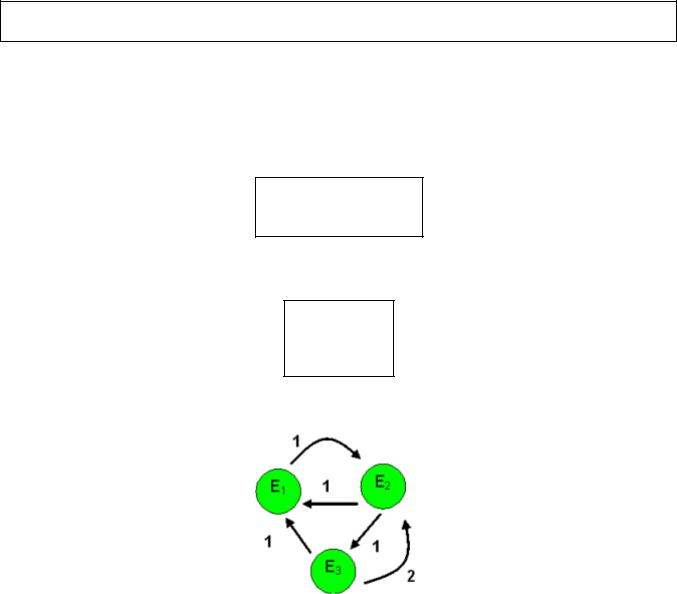
Напоминание:

Состояние Ej марковской цепи называется существенным, если куда бы мы ни ушли из него, всегда есть возможность вернуться

Теорема (признак эргодичности). Марковская цепь c непрерывным временем эргодична в том и только в том случае, если из любого существенного состояния можно добраться до любого другого существенного.

Финальные вероятности

Если цепь эргодична, то для любого начального вектора q(0) существует (одно и то же) финальное распределение вероятностей q*=q(∞):

q = lim q(t )

t →∞

Как его найти?

Теорема. Если цепь эргодична, то q* находится, как (единственное) решение системы уравнений

q A = 0

∑q j = 1

Задача. Эргодична ли марковская цепь из предыдущего примера? Если да, то найти финальные вероятности.

Решение. 1) Существенные состояния E1, E2, E3.

2)Из любого существенного есть путь до любого существенного Следовательно, цепь эргодична.

3)найдём финальные вероятности.

134

Замечание. Сравните этот ответ с

7.3 Системы массового обслуживания

Основные понятия

Примеры: Парикмахерская, магазин, билетная касса, очередь автомобилей на светофоре, заготовки деталей на конвейере и т.п.

Обычно нас интересуют:

1)среднее время ожидания обслуживания;

2)средняя длина очереди;

3)среднее количество занятых каналов;

4)вероятность отказа в обслуживании и т.п.

Системы массового обслуживания (СМО) бывают очень разнообразны. Возможные различия:

характеристики входящего потока заявок;

количество каналов обслуживания;

распределение времени обслуживания заявки;

количество фаз обслуживания;

наличие или отсутствие приоритетных заявок (“дисциплина обслуживания”);

характеристики очереди

ит.п.

Мы рассмотрим только простые СМО с

1)пуассоновским (“простейшим”) потоком заявок и

2)показательным временем обслуживания.

7.3.1 Пуассоновский поток заявок

I – интервал между заявками

Предполагается, что I – случайная величина, распределённая по показательному закону с параметром λ::

P(I<t)=1– e–λt

Параметр λ – “интенсивность потока заявок” = среднее число заявок в единицу времени. Средний интервал между заявками

135

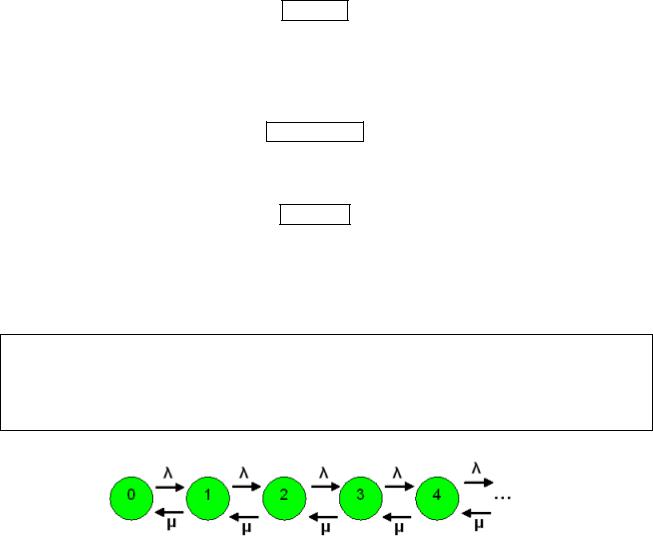
M I = 1/ λ

7.3.2 Распределение времени обслуживания

S – продолжительность обслуживания одной заявки.

Предполагается, что S – случайная величина, распределённая по показательному закону с параметром µ:

P(S<t) = 1–e–µt

Параметр µ – “интенсивность обслуживания” = среднее число заявок, обслуживаемых в единицу времени Средняя продолжительность обслуживания заявки

M S = 1/ µ

7.3.3Одноканальная СМО с неограниченной очередью

Входной поток заявок – пуассоновский с параметром λ.

Время обслуживания – показательное с параметром µ.

Один канал обслуживания.

Если канал занят, то пришедшая заявка ставится в очередь.

Размер очереди не ограничен.

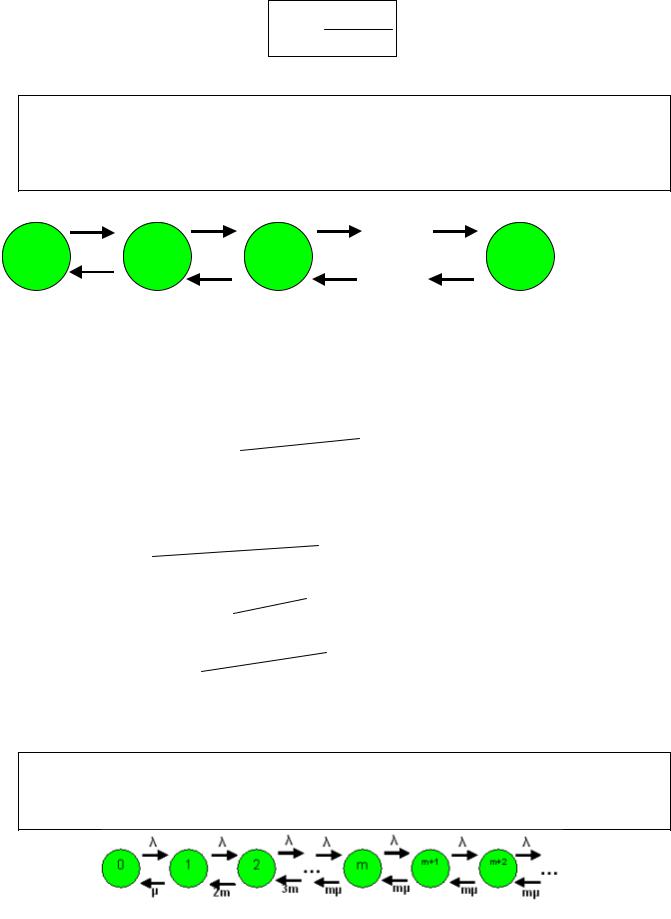
Будем рассматривать такую СМО как марковскую цепь с непрерывным временем

Матрица интенсивностей:

Как правило, наиболее интересно поведение системы за большой период времени. То есть нас интересуют финальные вероятности.

Отсюда получаем:

Если ρ≥1, то в системе будет неограниченно расти очередь. Поэтому рассматривается случай

ρ<1

qn = q0 ρ n

q0 + q1 + ... = 1 q0 (1+ ρ + ρ 2 + ...)= 1

1

q0 1− ρ = 1

Вероятность простоя системы

q0 = 1− ρ

Найдём другие характеристики этой СМО. Основные:

1.Средняя длина очереди ML.

2.Среднее количество заявок в системе Mn.

3.Среднее время ожидания обслуживания MW.

Средняя длина очереди

Пусть L – длина очереди. Это случайная величина, и надо найти её математическое ожидание

ML.

ML = 0 (q0 + q1 ) +1 q2 + 2 q3 + ... = ρ + 2ρ 2 + 3ρ 3 + 4ρ 4 + ...

Средняя длина очереди

ρ 2

ML =

1− ρ

Среднее число заявок в системе

Пусть n – число заявок в системе. Надо найти Mn.

Mn = 0 q0 +1 q1 + 2 q2 + ...

ρ

Mn =

1− ρ

Среднее время ожидания обслуживания

Теорема (формула Литтла). Среднее время ожидания обслуживания равно произведению средней длины очереди на средний интервал времени между приходящими заявками.

MW = ML MI

137

Для рассматриваемой СМО:

ρ 2

MW =

λ (1− ρ )

7.3.4Одноканальная СМО с ограниченной очередью

Входной поток заявок – пуассоновский с параметром λ.

Время обслуживания – показательное с параметром µ.

Один канал обслуживания.

Размер очереди не превосходит N

Если очередь заполнена, то пришедшая заявка отбрасывается

7.3.5Многоканальная СМО с неограниченной очередью

Входной поток заявок – пуассоновский с параметром λ.

m каналов обслуживания.

Время обслуживания каждым каналом – показательное с параметром µ.

Размер очереди не ограничен

Всё аналогично.

138

Условие отсутствия перегрузки системы

Среднее число занятых каналов

Mr = ρ

Среднее число заявок в системе

Mn = ML + Mr

Среднее время ожидания обслуживания

Задача. Составы поступают на техобслуживание. В среднем поступает 3 поезда в час. Имеется две бригады. Среднее время обслуживания состава одной бригадой равно 30 минут. Найти среднее время ожидания обслуживания.

Решение. m = 2, λ = 3 (поезда/час), µ = 2 (поезда/час)

ρ= λ = 1,5 < m

µ