
lect1_m4_vt_mrtus_CS_niy37
.pdf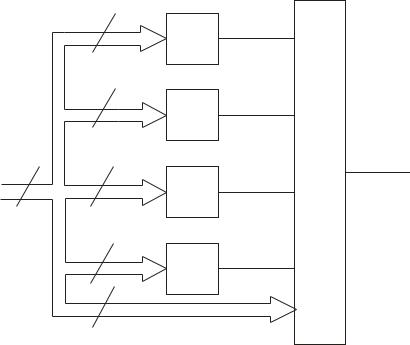
ров. Сложность ФАЛ, зависящей от 36 логических переменных и реализуемой в дизъюнктивной нормальной форме будет составлять 236/36 ≈ 19·108 контактов. Сложность той же ФАЛ, реализуемой по структуре, представленной на рис.3.8, составит 5·28/8 = 160 контактов. Как видно выигрыш составит ≈ 12·106 раз.
8
F1
8
F2
F5 y
36 |
8 |
F3
8
F4
4
Рис.3.8 4-х кратная декомпозициция ФАЛ
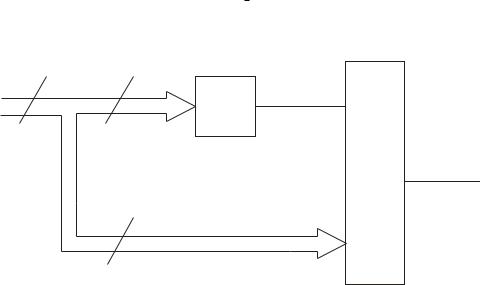
Однако к настоящему времени разработана и широко применяется в практике только структура, показанная на рис.3.9. Эта структура реализует простую (однократную) декомпозицию. Ниже будет рассмотрена простая разделительная функциональная декомпозиция, для которой справедливо:
Y U Z = X и Y ∩ Z = 0, где X – множество n всех входных переменных; Y – множество s входных переменных, по которым ведется простая разделительная декомпозиция; Z – множество r = n-s входных переменных.
Реализацию простой разделительной декомпозиции ведут для случая, когда 1 < s < n, так другие случаи тривиальны. Случаи s = 0 и s = n явно тривиальны. Случай s = 1 также тривиален, поскольку мы знаем, что любую ФАЛ можно разложить по одной переменной, используя теорему Шеннона:
f(xn 1;xn 2;...x;i;...x;0) xi f(xn 1;xn 2;...1;...x;0) xi f(xn 1;xn 2;...0;;...x;0) (3.25)
n
S
F1
X Y
F2 y
r=n-s |
Z |
рис.3.9. Простая разделительная функциональная декомпозиция
Итак, в соответствии с рис.3.9 для произвольной ФАЛ можно записать:

y f (xn 1;xn 2;...;x0 ) F2 (F1(ys 1 ys 2;...;y0 ),zr 1;zr 2;...;z0 ) (3.26)
Напомним, что декомпозиция ведется по переменным множества Y {ys 1 ys 2 ;...; y0 } как для полностью, так и для неполностью
определенных ФАЛ, но во всех случаях F1 и F2 – полностью определенные функции. Упростим выражение (3.26), используя векторные формы для переменных:
y F2 (F1 (Y ), Z ) |
(3.27) |
Так как F1(Y) является одной из переменных для F2, то в импликантах функции y переменная F1(Y) может встречаться только в ви-
де: 0, 1, F1(Y) и F 1 (Y ) . Если F1(Y) представить в виде таблицы истинности, то F1(Y) = 0 – это столбец из одних нулей; F1(Y) = 1 – это столбец из одних единиц; F1(Y) – произвольный столбец А или А, содержащий и нули и единицы; F 1 (Y) - произвольный столбец, инверсный столб-
цу А или А.
Разложим по теореме Шеннона (3.25) функцию (3.27) по переменной F1(Y).
y F2 (F1 (Y ), Z ) F1 (Y )[F2 (1, Z )] F1 (Y )[F2 (0, Z )] (3.28)
Преобразуем выражение (3.28) так, чтобы в явном виде выделить часть функции y, не зависящую от F1(Y).
y F(Y)[F(1,Z)] F1(Y)[F(0,Z)] F(Y)[F(1,Z)][F(0,Z) F2(0,Z)] |
|||||
1 |
2 |
2 |
1 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|||
F1(Y)[F2(0,Z)][F2(1,Z) F2(1,Z)] |
|
|
|
|
(3.29) |
|||||||
F(Y)F(1,Z)F(0,Z) F(Y)F(1,Z) |
|
|
|
|
||||||||
F2(0,Z) F1(Y)F(0,Z)F(1,Z) |
||||||||||||
1 |
2 |
2 |
1 |
2 |
|
2 |
2 |
|
||||
F1(Y)F2(0,Z)F2(1,Z)

В выражении (3.29) первое и третье произведения соседние и склеиваются по переменной F1(Y), поэтому окончательно получаем:
y F1 (Y )F2 (1, Z )F 2 (0, Z ) F 1 (Y )F2 (0, Z )F 2 (1, Z ) F2 (1, Z )F2 (0, Z )
(3.30)
Если любое из равенств (3.28) или (3.30) удовлетворяются, то простая разделительная декомпозиция по переменным множества Y существует, так как эти равенства представляют собой формы равенства
(3.25). |
Введем |
|
обозначения: |
1 (Z ) F2 (1, Z ) |
|
2 (0, Z ) ; |
|||
F |
|||||||||
0 (Z ) F2 (0, Z ) |
|
2 (1, Z ) ; x (Z ) F2 (1, Z )F2 (0, Z ) , |
тогда выра- |
||||||
F |
|||||||||
жение (3.30) примет вид: |
|
|
|
|
|||||
y F1 (Y ) 1 (Z ) |
|
1 (Y ) 0 (Z ) x (Z ) |
(3.31) |
||||||
F |
|||||||||
|
Итак, для нахождения простой разделительной функциональной |
||||||||
декомпозиции необходимо определить F1(Y), β1(Z), β0(Z), βx(Z). Для этого воспользуемся специальной формой карты Карно или декомпозиционной картой, построенной по следующему правилу:
- карта Карно должна содержать 2s строк и 2r= 2n-s столбцов, -строки соответствуют 2s наборам переменных множества Y, -столбцы соответствуют 2r= 2n-s наборам переменных множества Z.
Декомпозиция функции устанавливается на основе следующего положения, доказанного Ашенхерстом [12]: простая разделительная
декомпозиция |
функции |
|
f (xn 1 ; xn 2 ;...; x0 ) F2 (F1 ( ys 1 ys 2 ;...; y0 ), zr 1 ; zr 2 ;...; z0 ) |
су- |
|
ществует, если существует такая карта Карно с 2s строками и 2n-s столбцами, что каждый ее столбец может быть отнесен к одному из четырех типов: 1 – «все 0»; 2 – «все 1»; 3 – некоторый произвольный тип А и 4 –

инверсный ему тип А. Выбор обозначения столбца произволен, то есть за А можно взять и столбец А.
Рассмотрим простой пример. Пусть Х = {x3; x2; x1; x0}, Y = {x3; x2}, Z = {x1; x0}, тогда для ФАЛ, представленной картой Карно (см. рис.3.10), существует простая разделительная функциональная декомпозиция, так как первый слева столбец относится к типу А, второй – «все 1», третий - А и четвертый – «все 0». Отметим, что необязательно все четыре типа столбцов должны присутствовать в карте Карно. Например, в ней могут быть два столбца А, столбец «все 1» и столбец «все 0» и любые другие комбинации, важно, чтобы столбцы принадлежали к указанным выше четырем типам.
y |
x1 |
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
1 |
|
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
1 |
0 |
|
x2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
0 |
0 |
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
x0
А “1” А “0”
Рис.3.10. Карта Карно декомпозируемойФАЛ
Функция F1 (Y ) F1 (x3 ; x2 ) определяется из условия покры-
тия простыми импликантами, составленными из переменных множества Y, всех 1 в столбце А. В нашем примере F1 (Y ) x3 x2 x3 x2 .
Функция F 1 (Y ) определяется из условия покрытия всех 1 в столбце А
или инвертированием ранее полученного значения F1 (Y ) . Функция
F2 (1, Z ) определяется из условия покрытия простыми импликантами, составленными из переменных множества Z, всех 1 в строке, содержа-
щей их в столбцах А и «все 1». В нашем примере F2 (1, Z ) x1 . Функ-
ция F2 (0, Z ) определяется из условия покрытия всех 1 в строке , со-
держащей их |
в |
столбцах |
|
|
|
и «все 1». В |
нашем |
|
примере |
||||||
А |
|||||||||||||||
F2 (0, Z ) x0 |
. Очевидно, что |
|
2 (1, Z ) |
|
|
1 и |
|
2 (0, Z ) |
|
0 . |
|||||
F |
x |
F |
x |
||||||||||||
Так |
как |
1 (Z ) F2 (1, Z ) |
|
2 (0, Z ) , |
мы |
|
имеем |
||||||||
F |
|
||||||||||||||
1 (Z ) x1 x0 , что можно интерпретировать как покрытие простыми импликантами, составленными из переменных множества Z, столбца А или всех столбцов А, если их больше одного.
Так как 0 (Z ) F2 (0, Z )F 2 (1, Z ) , мы имеем
0 (Z ) x1 x0 , что можно интерпретировать как покрытие столбца А
или всех столбцов А, если их больше одного.
Так как x (Z ) F2 (1, Z )F2 (0, Z ) , мы имеем x (Z ) x1 x0 , что можно
интерпретировать как покрытие столбца «все 1» или всех столбцов «все 1», если их больше одного.
Итак, окончательно для y можно записать: y F1(Y) 1(Z) F1(Y) 0 (Z) x (Z) x3x2 x1 x0 x3x2 x1x0 x1x0 .
Если записать минимальное выражение для y, то из карты Карно (см.

рис.3.10) получим: y x3 x2 x0 x2 x1 x3 x1 , следовательно положе-
ние Ашенхерста устанавливает только наличие простой разделительной декомпозиции на основе специальной карты Карно. Полученную функцию y F1 (Y ) 1 (Z ) F 1 (Y ) 0 (Z ) x (Z ) в дальнейшем надо минимизировать.
