Примеры

Задача 1. Для реакции СО + H₂О  CO₂ + Н₂ при 1000K К_р = 0,48. Определить, в каком направлении пойдет процесс при следующих вариантах значений пар­циальных давлений компонентов:

Т а б л и ц а

№ варианта	атм.	атм.	атм.	атм.
1.1	2	6	3	5
1.2	5	2	7	3
1.3	1	3	2	6

Решение

Для случая, когда  = 0 и К⁰ = К_р, согласно (9.70) и (9.90) можно записать, что

.

Для каждого варианта находят численное значение

1. = 0,8; К_р = 0,48; 0,8  0,48, следовательно,  0.

Вывод: реакция самопроизвольно в указанном направлении не идет.

2.  0,48; К_р = 0,48; следовательно,  0.

Вывод: при данных парциальных давлениях реагирующих веществ система находится в состоянии равновесия.

1.3. = 0,25; К_р = 0,48; 0,25 < 0,48, следовательно,  0.

Вывод: реакция самопроизвольно протекает в прямом направлении.

Задача 2. Смешали 2,5 моль пропилена и 3,5 моль водорода в емкости объемом 1 л. К моменту установления равновесия при 600 К прореагировала половина взятого водорода. Начиная с какой концентрации будет происходить само­произвольное разложение пропана при этой температуре, если в реакцион­ной смеси содержится 3 моль пропилена и 4,5 моль водорода?

Решение

СН₃ - СН = СН₂ + Н₂  СН₃ - СН₂ - СН₃

при  = 0 2,5 моль 3,5 моль 0 моль

при _равн. (2,5 – 1,75) (3,5 – 1,75) 1,75 моль

К моменту установления равновесия в реакционной смеси содержится 0,75 моль пропилена, 1,75 моль водорода и 1,75 моль пропана, что в мольных долях составляет:

;

Таким образом,

; т.е. К_N = 5,67.

Согласно уравнению изотермы химической реакции (11.62)

.

Обозначим через число молей пропана, начиная с которого будет происходить его самопроизвольное разложение. В этом случае сумма числа молей всех компонентов исходной смеси составит:

3 + 4,5 + а = 7,5 + (моль), а их мольные доли:

; ;

т.е.

Для реакции самопроизвольного разложения пропана (реакция протекает в обратном направлении) F_V,Т0, т.е. .

Отсюда получаем неравенство: решение которого дает:= 5,77 моль; в расчете на объем, равный 1 л концентрация составит 5,77 моль/л.

Вывод: при концентрации пропана свыше 5,77 моль/л будет происходить процесс самопроизвольного его разложения.

11.7. Зависимость константы равновесия

химической реакции от температуры

Из изотермы-изобары химической реакции (11.89) следует, что .

Возьмем производную от этого выражения по температуре:

. (11.96)

Имея в виду, что и полагая, что в данном случае, аи V = RT, а V' = R, получаем следующее соотношение:

(11.97)

или . (11.98)

Вспомним уравнение Гиббса-Гельмгольца

и сравним его с полученным соотношением (11.98).

Из анализа следует, что

(11.99)

Это уравнение носит название уравнение изобары химической реакции (Вант-Гоффа).

По аналогии с предыдущим можно получить уравнение изохоры химической реакции:

(11.100)

Из уравнений (11.99) и (11.100) следует, что если для химической реакции имеет отрицательное значение (процесс экзотермический), то константа равновесия К⁰ с ростом температуры уменьшается. Если же 0 (процесс эндотермический), то константа равновесия К⁰ растет с увеличением температуры. Это же следует из принципа Ле-Шателье (раздел 11.6).

Разделим переменные в уравнении изобары Вант-Гоффа (11.99):

. (11.101)

1. Если Н не зависит от температуры в интервале от Т₁ до Т₂, то интегрирование уравнения (11.101) дает следующий результат:

(11.102)

или после подстановки пределов интегрирования

. (11.103)

После несложных преобразований получаем уравнение изобары в интегральной форме:

. (11.104)

Если при том же условии Н  f(Т) взять неопределенный интеграл от выражения (11.101), то получим:

. (11.105)

Это уравнение прямой линии в координатах: "lnК⁰ – 1/Т". Из графика и уравнения (11.105) следует, что тепловой эффект реакции можно определить графически:

lnK⁰

.



2. Если , но, то

(11.106)

или

. (11.107)

Таким образом:

. (11.108)

3. Если и, а зависимость эта имеет вид:

C_p = a + bT + cT² + c^T^-2, то

(11.109)

Примеры.

Задача 1. К⁰ реакции при 800 К равна 15,7. Определить температуру, при которой она равна 1570, если тепловой эффект этой реакции в данном интервале от температуры не зависит и равен -35 ккал/моль.

Решение

Запишем уравнение изобары в интегральной форме:

.

Примем, что Т₁ = 800 К, тогда

ln,

где R = 1,987 кал/(мольК).

Отсюда Т₂ = 662 К.

Если бы тепловой эффект был положительным, т.е. Н=

35 ккал/моль, то нетрудно показать, что в этом случае Т₂ = 1011 К.

Вывод: при Н  0 константа равновесия реакции растет при понижении температуры, а при Н  0, она растет при повышении температуры.

Задача 2. Определить К⁰ при 1000 К, если при 500 К для этой реакции она равна 50, а зависимость теплового эффекта от температуры имеет вид:

Решение

Запишем уравнение изобары в дифференциальной форме:

,

после разделения переменных оно принимает вид:

или

,

где R=8,314 Дж/(мольК).

.

Ответ: = 1,510^-3.

11.8. Термодинамическая активность и

коэффициент активности

Как было показано, химический потенциал компонента идеальной системы непосредственно связан с концентрацией компонента (11.46). Чтобы сохранить форму выражения химического потенциала для реальных систем, Льюис (1901) предложил ввести –величину, называемую термодинамической активностью (а) и определяемую соотношением:

(11.110)

или ; (11.111)

, (11.112)

где - химический потенциал компонента в стандартном состоянии, причем таком же, как и в идеальных системах; т.е. за стандарт принимается чистый компонент или гипотетический идеальный раствор компонента с единичной концентрацией.

Из определения термодинамической активности (11.112) следует, что эта величина, как и химический потенциал, характеризует термодинамические свойства компонента в системе и также является функцией концентрации, температуры и давления. По физическому смыслу ее можно представить как эффективную (энергетическую) концентрацию.

С помощью активности для любой реальной системы можно получить термодинамическое уравнение того же вида, что и для идеальной системы, а именно вместо концентрации компонента в выражение для химического потенциала вводят его активность.

Значение активности зависит как от выбора стандартного состояния, так и от выбора концентрационной шкалы. Соответственно этому химический потенциал компонента «i» имеет выражение:

; (11.113)

; (11.114)

, (11.115)

где а_i(N), а_i(С), а_i(m) – активности компонента i, соответствующие мольной доле, молярной и моляльной концентрациям, а также соответствующим стандартным состояниям.

Помимо активности Льюис ввел понятие коэффициента активности (), характеризующего отклонение состояния реальных растворов от идеальности. Для неэлектролитов коэффициент активности равен

. (11.116)

Коэффициент активности , характеризующий отклонение от идеальности по отношению к чистому веществу (совершенные идеальные системы), называют рациональным. Коэффициент активности, определяющий отклонение от идеальности по отношению к гипотетическому идеальному раствору с единичной концентрацией , называют концентрационным (молярнымили моляльным).

Подставив в уравнения (11.113)-(11.115) выражения для активности (11.116), получим:

; (11.117)

; (11.118)

или ; (11.119)

. (11.120)

Выразим химический потенциал компонента в идеальном растворе, соответствующем определенному стандартному состоянию, подобно уравнению (11.46)

(11.121)

. (11.122)

Тогда уравнения (11.117) и (11.118) можно представить в виде

(11.123)

(11.124)

или ; (11.125)

, (11.126)

т.е. коэффициент активности определяется энергией Гиббса переноса одного моля вещества из идеального раствора в реальный с той же концентрацией. Коэффициент активности компонента равен единице в идеальных растворах, как и в системах, выбранных за стандарт (в идеальных системах сравнения); концентрационный коэффициент активности стремится к единице при разбавлении системы.

Коэффициент активности компонентов в реальных растворах может быть как больше единицы ( положительное отклонение от идеальности), так и меньше ее (отрицательное отклонение от идеальности). Коэффициент активности, количественно характеризующий отклонение от идеальности, является одним из важнейших термодинамических параметров для реальных систем, так как именно определение отклонения от идеальности – основная задача термодинамически реальных систем.

Как уже упоминалось ранее, в термодинамике газообразных систем химический потенциал обычно выражают не через концентрации, а через парциальные давления газов. Для идеальных газовых смесей согласно (11.51) при постоянной температуре химический потенциал компонента i равен

.

Чтобы аналогичным образом записать химический потенциал для реальных систем, используют термодинамический параметр – фугитивность (летучесть) – f, имеющий размерность давления. С использованием этого параметра выражение химического потенциала для реальных систем приобретает следующий вид:

(11.127)

Фугитивность учитывает межмолекулярные взаимодействия в газах (т.е. отклонения от идеальности) и поэтому зависит как от температуры, так и от давления аналогично химическому потенциалу.

Отношение фугитивности к давлению называют коэффициентом фугитивности:

, (11.128)

который характеризует отклонение свойств реального газа от свойств идеального газа, подобно коэффициенту активности для растворов.

При снижении давления межмолекулярное взаимодействие уменьшается и газ приобретает свойства идеального газа; соответственно фугитивность становится равной давлению, а коэффициент фугитивности стремится к единице:

;. (11.129)

Как следует из соотношений (11.127)-(11.129), за стандартное состояние реальных газов принимается газ, который имеет давление и фугитивность, равные единице (1 атм), или его гипотетическое состояние (так как реальный газ при таком давлении не является идеальным). Коэффициент фугитивности в стандартном состоянии, очевидно, также равен единице. Соответственно стандартный химический потенциал не зависит от давления; зависит от давления только фугитивность.

Фугитивность компонента (f) непосредственно связана с его активностью (а), в том числе и для летучего компонента жидкого раствора. Так, химический потенциал летучего растворителя (компонент 1) в растворе и химический потенциал его пара, находящегося в равновесии с раствором (_ж = _пар) – соответственно записываются так:

, (11.130)

. (11.131)

Стандартный химический потенциал чистого растворителя, или пара над чистым растворителем (в состоянии равновесия) равен

. (11.132)

Подставляя значение из (11.132) в (11.131) получим:

, (11.133)

т.е. активность летучего компонента равна отношению равновесных фугитивностей его пара над раствором и над чистым компонентом.

Как отмечалось, введение активности позволяет на основании определений одного из свойств раствора вычислить другие его свойства.

Рассмотрим способ, при помощи которого по известной активности компонента бинарного раствора находится активность другого компонента. Для бинарного раствора N₁+N₂=1 и, соответственно, dN₁=-dN₂. Вспомним уравнения Гиббса-Дюгема (11.17), которое для химического потенциала предстает в виде (11.19) для бинарного раствора:

N₁d₁+N₂d₂=0

или

. (11.134)

Таким образом, если известна величина как функция N₁, то можно рассчитать . Возьмем, например, в качестве парциальной молярной величины химический потенциал в виде (11.51):

.

Тогда из предыдущего уравнения (11.134) следует:

, (11.135)

поскольку , R и Т – постоянные.

Кроме того, по определению (11.133)

и. (11.136)

Логарифмирование этих выражений

;

и их последующее дифференцирование соответственно по N₁ и N₂ при постоянных Р и Т приводят к уравнениям:

;

(11.138)

поскольку и- постоянны.

После подстановки этих равенств в уравнение (11.135) получаем:

. (11.139)

Это уравнение может быть обобщено на раствор, содержащий несколько компонентов:

(11.140)

Если бинарный раствор близок к разбавленному, то с учетом (11.136) уравнение (11.139) может быть представлено в более простом виде (при постоянных Р и Т):

N₁dlnа₁ = - N₂dlnа₂ . (11.141)

Из изложенного следует, что для определения активности одного компонента необходимо знать зависимость активности второго компонента от состава и активность первого компонента при какой-либо одной концентрации N₁. Пусть, например, известна зависимость активности летучего компонента а₂ от его концентрации N₂. Тогда для вычисления а₁ следует проинтегрировать уравнение (11.141) в пределах от концентрации N₁, где известна а₁, до искомой концентрации N^/₁

; (11.142)

. (11.143)

Первый компонент является растворителем и (при N=1) а₁=1. Следовательно, второй член в левой части уравнения (11.143) равен нулю.

Таким образом,

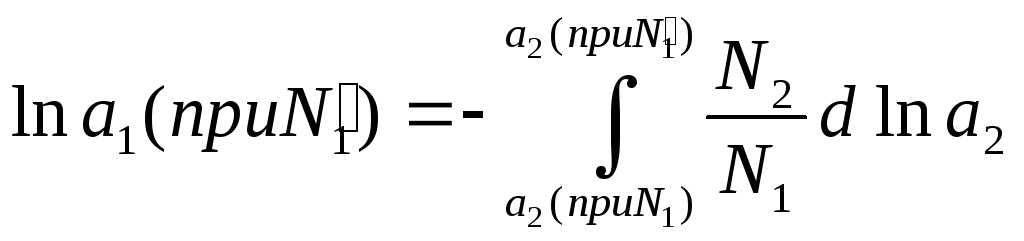. (11.144)

Этот интеграл обычно определяют графически, откладывая по оси ординат отношение N₂/N₁, а по оси абсцисс ln а₂, как это показано на рис 11.4.

N₂/N₁

А

D

С

В

- ln а₂ 

Рис. 11.4. Графическое определение активности

Величина интеграла равна заштрихованной площади под кривой АС, лежащей правее вертикали DВ, до точки, где ln а₂ соответствует N₁=1. Однако в этой области из-за малости а₂ графическое интегрирование неточно (ln а₂ ). Избежать этой неточности можно с помощью простого приема, основанного на справедливом для бинарного раствора равенстве, ранее упоминавшемся, dN₁=-dN₂. Умножив и разделив обе части этого равенства на N₁ и N₂ соответственно, получим

N₁d lnN₁ = -N₂d lnN₂. (11.145)

После почленного вычитания этого выражения из уравнения (11.141) получаем:

(11.146)

или N₁d ln₁ = -N₂d ln₂ . (11.147)