
- •Brief Contents
- •Contents
- •Preface
- •Who Should Use this Book
- •Philosophy
- •A Short Word on Experiments
- •Acknowledgments
- •Rational Choice Theory and Rational Modeling
- •Rationality and Demand Curves
- •Bounded Rationality and Model Types
- •References
- •Rational Choice with Fixed and Marginal Costs
- •Fixed versus Sunk Costs
- •The Sunk Cost Fallacy
- •Theory and Reactions to Sunk Cost
- •History and Notes
- •Rational Explanations for the Sunk Cost Fallacy
- •Transaction Utility and Flat-Rate Bias
- •Procedural Explanations for Flat-Rate Bias
- •Rational Explanations for Flat-Rate Bias
- •History and Notes
- •Theory and Reference-Dependent Preferences
- •Rational Choice with Income from Varying Sources
- •The Theory of Mental Accounting
- •Budgeting and Consumption Bundles
- •Accounts, Integrating, or Segregating
- •Payment Decoupling, Prepurchase, and Credit Card Purchases
- •Investments and Opening and Closing Accounts
- •Reference Points and Indifference Curves
- •Rational Choice, Temptation and Gifts versus Cash
- •Budgets, Accounts, Temptation, and Gifts
- •Rational Choice over Time
- •References
- •Rational Choice and Default Options
- •Rational Explanations of the Status Quo Bias
- •History and Notes
- •Reference Points, Indifference Curves, and the Consumer Problem
- •An Evolutionary Explanation for Loss Aversion
- •Rational Choice and Getting and Giving Up Goods
- •Loss Aversion and the Endowment Effect
- •Rational Explanations for the Endowment Effect
- •History and Notes
- •Thought Questions
- •Rational Bidding in Auctions
- •Procedural Explanations for Overbidding
- •Levels of Rationality
- •Bidding Heuristics and Transparency
- •Rational Bidding under Dutch and First-Price Auctions
- •History and Notes
- •Rational Prices in English, Dutch, and First-Price Auctions
- •Auction with Uncertainty
- •Rational Bidding under Uncertainty
- •History and Notes
- •References
- •Multiple Rational Choice with Certainty and Uncertainty
- •The Portfolio Problem
- •Narrow versus Broad Bracketing
- •Bracketing the Portfolio Problem
- •More than the Sum of Its Parts
- •The Utility Function and Risk Aversion
- •Bracketing and Variety
- •Rational Bracketing for Variety
- •Changing Preferences, Adding Up, and Choice Bracketing
- •Addiction and Melioration
- •Narrow Bracketing and Motivation
- •Behavioral Bracketing
- •History and Notes
- •Rational Explanations for Bracketing Behavior
- •Statistical Inference and Information
- •Calibration Exercises
- •Representativeness
- •Conjunction Bias
- •The Law of Small Numbers
- •Conservatism versus Representativeness
- •Availability Heuristic
- •Bias, Bigotry, and Availability
- •History and Notes
- •References
- •Rational Information Search
- •Risk Aversion and Production
- •Self-Serving Bias
- •Is Bad Information Bad?
- •History and Notes
- •Thought Questions
- •Rational Decision under Risk
- •Independence and Rational Decision under Risk
- •Allowing Violations of Independence
- •The Shape of Indifference Curves
- •Evidence on the Shape of Probability Weights
- •Probability Weights without Preferences for the Inferior
- •History and Notes
- •Thought Questions
- •Risk Aversion, Risk Loving, and Loss Aversion
- •Prospect Theory
- •Prospect Theory and Indifference Curves
- •Does Prospect Theory Solve the Whole Problem?
- •Prospect Theory and Risk Aversion in Small Gambles
- •History and Notes
- •References
- •The Standard Models of Intertemporal Choice
- •Making Decisions for Our Future Self
- •Projection Bias and Addiction
- •The Role of Emotions and Visceral Factors in Choice
- •Modeling the Hot–Cold Empathy Gap
- •Hindsight Bias and the Curse of Knowledge
- •History and Notes
- •Thought Questions
- •The Fully Additive Model
- •Discounting in Continuous Time
- •Why Would Discounting Be Stable?
- •Naïve Hyperbolic Discounting
- •Naïve Quasi-Hyperbolic Discounting
- •The Common Difference Effect
- •The Absolute Magnitude Effect
- •History and Notes
- •References
- •Rationality and the Possibility of Committing
- •Commitment under Time Inconsistency
- •Choosing When to Do It
- •Of Sophisticates and Naïfs
- •Uncommitting
- •History and Notes
- •Thought Questions
- •Rationality and Altruism
- •Public Goods Provision and Altruistic Behavior
- •History and Notes
- •Thought Questions
- •Inequity Aversion
- •Holding Firms Accountable in a Competitive Marketplace
- •Fairness
- •Kindness Functions
- •Psychological Games
- •History and Notes
- •References
- •Of Trust and Trustworthiness
- •Trust in the Marketplace
- •Trust and Distrust
- •Reciprocity
- •History and Notes
- •References
- •Glossary
- •Index

|
|
|
|
The Portfolio Problem |
|
133 |
|
you on if you promise to let me make 100 such bets.” The willingness to take on 100 such bets but not one suggests that the colleague’s preferences are not independent of segmentation. Rather, he appears willing to take on many undesirable bets in violation of the basic rational choice model.
It is notable that the colleague cites the pain of loss from $100 dollars dominating the gain of $200, suggesting that loss aversion plays some role. Moreover, it is clear that the desirability of each individual gamble depends on whether the decision is made independently or jointly with the decision to take on many other similar gambles. Samuelson saw this as potential evidence that behavior did not conform to expected utility or that people have difficulty in understanding how concepts such as diversifying risk really works. In this case, the probability of loss is much smaller with 100 gambles (less than 1 percent) than with 1 gamble (50 percent), but the potential magnitude of the losses is much larger ($10,000 vs. $100). The increase in potential losses must dominate the reduced probability of losses under the expected utility model.
Thus, diversifying investments can reduce the probability of a loss, but if the investments are not desirable to begin with, diversification cannot magically make a bad gamble good. Consider a group of two of Samuelson’s gambles. In this case, the colleague faces a 0.25 probability of losing $200, a 0.50 probability of gaining $100, and a 0.25 probability of gaining $400. I suspect that many readers at this point might consider this gamble much more attractive than the original gamble. Nonetheless, in almost all reasonable cases, turning down the original gamble should lead a rational decision maker to reject this latter gamble under expected utility theory. Why then does grouping the gambles together seem to make them more attractive?
The Portfolio Problem
Often we might want to consider something similar to the stock portfolio problem, where a person might decide how much to invest in several activities at once. For example, suppose that an investor can divide her wealth between two assets. One is a safe asset that returns exactly the amount invested with certainty. Thus, if an investor invests x in the safe asset, she will be able to obtain x at the time she sells this asset. The second is a risky asset, such that every dollar invested in the asset will be worth z at the time of sale, where z is a random variable. Suppose that the expected value of z is μ > 1. Then, the investor with wealth w who wishes to maximize her expected utility of investing in the safe and risky assets will solve
max E u w − wz + wzz |
6 12 |
wz |
|
where w is wealth to be invested and wz is the amount of wealth invested in the risky asset. The solution to this problem is approximated by:
wz = |
μ − 1 |
, |
6 13 |
|
|||
|
σ2RA |
|
|
where RA is the coefficient of absolute risk aversion and the value σ2 = E x − μ
x − μ 2
2 is commonly called the variance of z. The variance measures how dispersed the values of z
is commonly called the variance of z. The variance measures how dispersed the values of z

|
|
|
|
|
134 |
|
BRACKETING DECISIONS |
are—how far away from the mean we believe the value of z may be. The higher the value of σ2, the riskier the investment. Thus, the higher is the aversion to risk, the lower the investment in the risky asset. Similarly, the riskier the asset (the higher the variance), the lower the investment in the risky asset. As well, increasing the expected payout of the risky asset relative to the safe asset increases investment in the risky asset. (The interested reader can see the derivation in the Advanced Concept box, The Portfolio Problem.)
EXAMPLE 6.2 The Equity Premium Puzzle
The return from investing in stocks has historically been far superior to the return from investing in bonds. For example, from 1871 until 1990 the return on stocks was about 6.5 percent per year, whereas the return on bonds was around 1 percent. Over any longterm investment horizon (more than 30 years), stocks overwhelmingly outperform bonds—often by more than seven times—leading one to wonder why anyone would ever invest in bonds. Bonds are often used as a relatively risk-free investment, though they still contain significant risk. Bonds pay a fixed nominal rate of return so long as the issuing body remains obligated. This issuing body may be a firm or a government. Thus, if the issuing body goes bankrupt it might default. As well, inflation can erode the rate of return over the life of the bond. Nonetheless, if we were to think about this problem in terms of the portfolio problem presented above, the rate of return, μ, would be about 7. Further, the commonly assumed range for the level of relative risk aversion is about 1 to 3. Thus, absolute risk aversion is between 1 and 3 divided by the total amount of wealth, a truly small number. If we assume 3, then we could rewrite the formula (equation 6.13) as
wz = |
3w |
, |
6 14 |
σ2 |
where wz is the optimal amount of money to invest in stocks, σ2 is the variance in return of the stock portfolio, and w is the total amount of wealth.
The variance of the stock portfolio depends on the time horizon. If we consider the long horizon on a representative portfolio of stocks, this variance is actually quite low, well below 3. In this case, the optimal investment is greater than the total wealth to be invested, leaving no room for bonds. More generally, economists estimate that the level of relative risk aversion necessary to induce one to purchase any bonds must be about 30, ten times the reasonable upper bound used by economists. To put this in perspective, consider a gamble with 0.50 probability of ending with $100,000 of wealth and a 0.50 probability of ending with $50,000 of wealth. The investor must be willing to pay at least $50,000 for this gamble, because this is the lowest possible outcome. An investor with relative risk aversion of 30 would have a certainty equivalent for this gamble of just $51,209 despite the expected value of $75,000. Thus, a 50 percent chance of winning an extra $50,000 is worth only $1,209 to her. This is an astounding and unreasonable level of risk aversion. Thus, one might reasonably conclude that stock prices reflect a violation of the rational model of decision under uncertainty.

|
|
|
|
Narrow versus Broad Bracketing |
|
135 |
|
Narrow versus Broad Bracketing
One could explain both examples 1 and 2 through a combination of loss aversion and a model of decision bracketing. Bracketing refers to the grouping of decisions. If a set of choices are made so as to take account of the impact of each individual choice in the set on all other choices, we say they are bracketed together. As a simple example, if I choose to have a light breakfast, I might prefer to have a larger lunch. If when I decide to have a light breakfast I anticipate the need for a larger lunch, my breakfast and lunch decisions are bracketed together. If I ignore the impact of my breakfast on lunch, these decisions are bracketed separately. A decision is narrowly bracketed if it is bracketed together with only a small set of decisions. A decision is broadly bracketed if it is bracketed with a larger set of decisions. Generally a person brackets decisions based upon how they are framed. Thus, if the diner is presented several decisions at once (e.g., which entrée and side dishes she would like at dinner), they may be bracketed together. Alternatively, if decisions are presented sequentially (e.g., what she will eat for breakfast, lunch, and dinner), they will most likely not be bracketed together.
Shlomo Benartzi and Richard Thaler note that one could easily explain the behavior of Samuelson’s colleague through an appeal to loss aversion and bracketing. Suppose for example, that the person has a value of money function that is given by
v x = |
x |
if |
x ≥ 0 |
2.5x |
if |
6 15 |
|
|
x < 0. |
Then, replacing the utility of wealth with the value function, the expected utility of the gamble in example 1 is E v
v x
x = 0.5
= 0.5  v
v 200
200 + 0.5
+ 0.5  v
v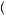 − 100
− 100 = 100 − 125 = − 25. Thus, the person would turn down the gamble because it would result in a negative value. Also, if the person were forced to take one gamble and then asked if she would take a second, the calculation would be the same. This is because even if the person had experienced seven gains of $200 in a row, she would evaluate a loss on the eighth gamble as a loss, thus resulting in a much more severe penalty than the reduction of a gain. From whatever the starting point, the potential loss of $100 looms larger than the potential gain of $200, just as Paul Samuelson’s colleague speculated, resulting in negative expected utility. Instead, suppose the person were offered to play two of the gambles jointly, thus leading to a more broadly bracketed choice. In this case, the expected value is E
= 100 − 125 = − 25. Thus, the person would turn down the gamble because it would result in a negative value. Also, if the person were forced to take one gamble and then asked if she would take a second, the calculation would be the same. This is because even if the person had experienced seven gains of $200 in a row, she would evaluate a loss on the eighth gamble as a loss, thus resulting in a much more severe penalty than the reduction of a gain. From whatever the starting point, the potential loss of $100 looms larger than the potential gain of $200, just as Paul Samuelson’s colleague speculated, resulting in negative expected utility. Instead, suppose the person were offered to play two of the gambles jointly, thus leading to a more broadly bracketed choice. In this case, the expected value is E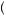 v
v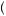 2x
2x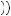 = 0.25
= 0.25  v
v 400
400 + 0.5
+ 0.5  v
v 100
100 + 0.25v
+ 0.25v − 200
− 200 = 100 + 50 − 125 = 25. Thus, the person would choose to take two gambles together, although she would not choose to take any single gamble individually. The same would hold true for 100 of these gambles.
= 100 + 50 − 125 = 25. Thus, the person would choose to take two gambles together, although she would not choose to take any single gamble individually. The same would hold true for 100 of these gambles.
Note that one of the reasons the value function can explain this choice is that the value function in equation 6.15 violates the condition required by Samuelson. Because the value function is linear both above and below, the individual gamble would be accepted if the gambler were to interpret all outcomes as gains or all outcomes as losses. For example, if all were interpreted as gains, all values would be treated as if x > 0 and v x
x = x. The expected value would be E
= x. The expected value would be E v
v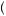 x
x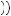 = 0.5
= 0.5  200 + 0.5
200 + 0.5 
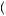 − 100
− 100 = 50. The same thing would be found if all values were considered losses. Thus, the range over
= 50. The same thing would be found if all values were considered losses. Thus, the range over

|
|
|
|
|
|
|
|
|
136 |
|
BRACKETING DECISIONS |
|
|
||
|
|
which the gamble would be rejected is small, encompassing just the gambles that span |
|||||
|
|
the kink in the value function. |
|
|
|||
|
|
|
Alternatively, consider a commonly used utility function under the rational model, |
||||
|
|
u x = 1 − exp |
− RAx . This is commonly referred to as the constant absolute |
risk |
|||
|
|
aversion utility function because this function displays absolute risk aversion of RA for |
|||||
|
|
all values of x. No matter what parameter of absolute risk aversion we choose, u 0 |
= 0, |
||||
|
|
so the gambler would take the gamble if and only if expected utility is positive. If we |
|||||
|
|
choose the parameter RA = 0.1, the expected utility of the single gamble is negative, |
|||||
|
|
E u x |
= − 11012.23, as is the expected utility of two of the gambles, E u 2x |
= |
|||
|
|
|
− 1.2 × 108. If we were to arbitrarily add $200, the maximum change in wealth result- |
||||
|
|
ing from one gamble, to the gambler’s wealth before taking the gamble, the new |
|||||
|
|
utility function would be given by u x + 200 = 1 − exp − RA x + 200 |
, with the utility |
||||
|
|
resulting from rejecting any gamble equal to approximately 1. In this case, expected |
|||||
|
|
utility of a single gamble is slightly less than 1, so that the gamble would still be rejected. |
|||||
|
|
We can infer that the single gamble would be rejected over any starting level of wealth |
|||||
|
|
between 0 and 200. |
|
|
|||
|
|
|
It is possible to find parameters that lead to accepting multiple gambles and rejecting |
||||
|
|
the initial gamble. However, these parameters violate Samuelson’s conditions that the single |
|||||
|
|
gamble would be rejected in a region of wealth w − 200, w + 200 . If instead, we chose |
|||||
|
|
RA = 0.00481211825, the expected utility of the single gamble is E u x |
= − 1.1 × 10− 10, |
||||
|
|
suggesting rejection of the single gamble. The expected utility of two of the gambles is |
|||||
|
|
E u 2x |
= 2.1 × 10− 10, suggesting acceptance of the joint gamble. However, the single |
||||
|
|
gamble |
would be accepted if we were to arbitrarily add $200 to the initial wealth, |
||||
|
|
E u x + 200 |
> u 200 , and thus Samuelson’s condition does not hold. |
|
|
||
Benartzi and Thaler propose that the equity premium puzzle might also be due to a combination of loss aversion and narrowly bracketed investment decisions. The length of the planning horizon in investment affects the variance or variation in the return of the portfolio. Although bonds have a slow and stable return with relatively constant variation, stocks have high return but relatively high variation in the near term. Thus, on any given day the return from a diverse bundle of stocks can range from −10 percent to +10 percent, and the variance of returns for the same stocks over a 30-year investment period is quite small. This is somewhat like gambling on one coin flip versus gambling on the average outcome of a series of 100 coin flips. Although the average return is the same, the variance is substantially reduced. Thus, with a long planning horizon, the difference in returns for stocks and bonds should lead one to invest all of one’s assets in stocks.
If the planning horizon is short, the variance is much larger relative to the average return, thus the right side of equation 6.14 may be smaller than the total amount of wealth to be invested, leading one to hold bonds as well. Benartzi and Thaler hypothesize that people narrowly bracket their investment decisions relative to their planning horizon. Thus, although an investor may be investing for a 30-year period, she might evaluate her portfolio much more often and invest as if her planning horizon was much shorter. Using simulations based on stock and bond return data, they find that the returns on stocks relative to bonds are consistent with loss-averse investors evaluating (or bracketing) their decisions on an annual basis. Because they behave as if they are maximizing their expected utility of investing over a one-year period, rather than the longer period they may be investing in, they could potentially be made better off by reducing their holding of bonds and increasing their
|
|
|
|
Narrow versus Broad Bracketing |
|
137 |
|
holding of stocks. Nonetheless, each year when they evaluate the return, the variation and losses lead them to purchase bonds and ignore their longer planning horizon.
Richard Thaler, and a group of distinguished colleagues, conducted a series of experiments to test for time bracketing in investments. The theory of bracketing suggests that if people evaluate their investments regularly they will bracket narrowly, and they will tend toward less-risky investments no matter what the planning horizon. Thus, people are willing to take on larger risks over long periods of time if they are not allowed to evaluate the outcomes throughout the duration. When not allowed to evaluate, the investor is essentially facing a compound gamble consisting of n groups of the singleperiod gamble, where n is the number of periods before they can evaluate. When allowed to evaluate, it is like facing n individual gambles sequentially. Broad bracketing can lead to a more favorable view of the gamble.
A group of 80 participants were asked to allocate 100 units of a portfolio between two investments, fund A and fund B. They were told that the returns per period for a unit of fund A would be drawn from a distribution with a mean of 0.25 percent and a standard deviation (defined as the square root of the variance) of 0.177 percent. Fund B returns per period were drawn from a distribution with a mean return of 1.00 percent and a standard deviation of 3.54 percent. Thus B was much riskier, yet it had a mean return of about four times that of A.
Participants were randomly placed into treatments. Participants in the first treatment were asked to make 200 decisions, with one decision following each period and after being able to observe the returns for that period. The second treatment required participants to make 25 decisions, with each decision binding for eight periods. The third treatment required participants to make five decisions, which would be binding for 40 periods. No matter which treatment was applied, the same set of random draws for A and B were used, so that all subjects in all treatments were viewing the same return history in any decision period. Subjects would only observe returns when they were allowed to make a decision. Those in the condition that required a decision every period placed more than 50 percent of their portfolio in A, the lower-risk option, over the course of the experiment. Those making fewer decisions placed less than 50 percent of their portfolio in the safer option, between 30 percent and 40 percent on average. Thus, by simply manipulating the frequency of evaluation, the researchers found that subjects become more sensitive to risk.
The notion that people would choose long-term investments based on short-term priorities is closely related to the notion of melioration. Melioration is a concept from experimental psychology whereby someone chooses the option that yields the highest utility in the current period, ignoring the impacts of their decision on choices and experiences available in future periods. Melioration has been explained using many different behavioral models. Decision bracketing provides one explanation, whereby the person is given a choice framed in such a way that future consequences are altogether ignored. For example, in the case of investment decisions, the investor makes investments that are attractive in the near term, ignoring the properties of the potential investments in the longer term. Alternative models of melioration are presented in Part III of this book examining time discounting.
Thus far we have discussed the possibility that bracketing decisions by time sequence can affect investment decisions. But it is also possible to bracket decisions by individual
|
|
|
|
|
|
|
138 |
|
BRACKETING DECISIONS |
|
|
|
|
investments in the portfolio. If an investor uses broad bracketing in this context, she |
|||
|
|
might solve |
|
|
|
|
|
|
|
n |
|
|
|
|
max E C + v |
xizi , |
6 16 |
|
|
|
x1, ,xn |
i = 1 |
|
|
|
|
|
|
|
|
|
subject to the constraint |
|
|
|
|
|
|
|
n |
|
|
|
|
C = w − |
xi, |
6 17 |
|
|
|
i = 1 |
|
|
where xi represents the investment in asset i, zi is the random variable that represents the
n
return from asset i, v  is a loss-averse value function with a reference point of i = 1 xi (in other words, the reference point is the amount invested), C represents money spent in current consumption (the utility of consuming C is equal to C), and w is the total amount of wealth. Here I have suppressed the intertemporal nature of investment for simplicity.
is a loss-averse value function with a reference point of i = 1 xi (in other words, the reference point is the amount invested), C represents money spent in current consumption (the utility of consuming C is equal to C), and w is the total amount of wealth. Here I have suppressed the intertemporal nature of investment for simplicity.
In this case, the investor will experience an overall loss if the total return is less than
n
i = 1 xi. The kinked shape of the value function leads the investor to display risk aversion by choosing an investment portfolio that displays a lower level of risk but also possibly a lower return. Nonetheless, it is possible that several of the stocks in the optimal portfolio will be quite risky because their risk will be averaged with the other n investments. The probability of an overall loss becomes quite small if n is large, the returns are all positive on average, and the investment returns are independent of one another. This result is similar to the reduction in the probability of loss obtained in Samuelson’s gamble when n is increased. If the portfolio decisions are narrowly bracketed, however, we may write the problem as
|
n |
|
|
max E C + |
|
v xizi |
6 18 |
x1, , xn |
i = |
1 |
|
|
|
with the same budget constraint. The difference is that now each investment is evaluated by itself in the value function with a reference point of xi. In this case, the investor becomes severely averse to loss in any single investment. Here each investment is evaluated based on gains or losses in the investment. Thus, the investor would feel severe pain for a $1 loss in investment i even if the overall return of the portfolio is positive. This focus on the individual stock return means the investor cannot fully take advantage of diversification but rather seeks that all investments will have minimal risk of losses.
Nicholas Barberis and Ming Huang find that this alternative form of narrow bracketing is quite consistent with the patterns of investment decisions in the market, leading to the highly inflated returns on stocks that are necessary to justify the purchase of relatively risky investments among the loss averse when relatively safe investments are available. Clearly, one can obtain better returns by broad bracketing than by narrow bracketing. Barberis and Huang suppose that equation 6.18 might prevail because people take a loss on a stock personally. One might feel the individual loss as an indication of one’s investing ability and a failure of one’s own decision making.
