Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

metodichkaFTUG_chast1

.pdf

Скачиваний:

Добавлен:

26.03.2016

Размер:

2.68 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 137 8 9 10 11 12 13 > Следующая >>>

										i			j		k
		M R, BA							1			4		4		8i 9 j 7k ,											а		его						модуль
															1
									2			1			1


	M		64 81 49 194 .

	Пример 4. Даны координаты вершин треугольной пирамиды:
	A 1, 2,3 ,				B 0,1, 2 ,										C 1,1,3 ,							D 0, 0,3 .							Найти						объем
пирамиды, ее высоту, опущенную из вершины D, угол между
вектором AD и гранью, в которой лежат векторы АВ и АС .
	Решение. Найдем векторы:																	AB 1, 1, 1 ,											AC 0, 1, 0 ,
	AD 1, 2,0 .
	Объем пирамиды
								1													1	1		1			1				1
																						1		1			1
					V							AB, AC, AD										0 1 0										.


							6												6			1		2						6
							6												6			1		2		0				6
	С другой стороны,													объем пирамиды V													1	S		h ,				где		h −
	С другой стороны,													объем пирамиды V														S	осн	h ,				где		h −
																										3			осн
																										3
высота,					опущенная									из		вершины							D,			Sосн					−			площадь
треугольника,							построенного													на		векторах							АВ					и		АС :
	S		1	AB, AC						.
			1
			2
	осн		2
	осн
							i					j			k

		AB, AC																						1	AB, AC								1				2
						1					1			1		i k , S																			i k			.

																								2									2
																						осн		2									2				2
																						осн
							0				1			0


Тогда высота h									3V					1			2			.
Тогда высота h																				.
										Sосн				2			2

Угол между вектором и гранью ABC найдем по формуле


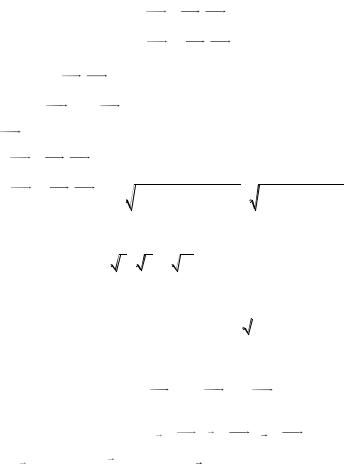
											AD, AB, AC
				2 arccos																						,
													AD					AB, AC
													AD					AB, AC

так как вектор			AB, AC					перпендикулярен грани, в которой

лежат векторы			AB	и	AC . Угол												между						этим вектором										и
вектором AD находим по формуле (2.9):
			AB, AC													1 1 2 0 0 1
cos	AD,		AB, AC													1 1 2 0 0 1
cos
										1					2			2			2			2			1		2		2		2
	AD	AB, AC													2						2	0							2	0		1
	AD	AB, AC																				0								0		1
							1									1			.


							5					2				10
							5					2				10
Очевидно, что искомый угол
				arccos				cos										arccos									1	.
																											1


			2													2									10
Пример 5. Проверить, лежат ли в одной плоскости точки
A 0, 0, 1 , B 2, 1, 3 , C 1, 2, 2 ,																		D 3, 4, 8 .												Найти
линейную зависимость вектора													AB				от			AC			и				AD ,		если это
возможно.
Решение. Найдем три вектора: a AB,																				b AC, c AD .
	a 2, 1, 2 , b 1, 2, 3 , c 3, 4, 7 .
Три вектора лежат в одной плоскости, если они
компланарны, т. е. их смешанное произведение равно нулю:
						2			1			2
						2			1			2
						1	2							3			0 .
						3			4			7

Следовательно, эти три вектора линейно зависимы.

Найдем линейную зависимость	AB от	AC и AD:
a b c . Векторному равенству	a b c	соответствует

следующее условие

2, 1, 2 1, 2, 3 3, 4, 7 .

Из определения равенства двух векторов имеем систему линейных уравнений

3 2,2 4 1,

3 7 2,

решая которую, получим			1	, т.е.	a	1	b	1	c .
		2			2			2
	Задания для решения в аудитории
I уровень
1. Заданы	векторы	a1 (3, 1, 2)		и	a2 (1, 2, 1) . Найти
координаты	векторов:	а) a1 , a2 ;		б)	2a1 a2 , a2 ; в)

2a1 a2 , 2a1 a2 .

и (a1 , a2 ) 2 / 3 . Вычислить: а)

a1,a2

2a1 a2 ,a1 2a2

; в)

a1 3a2 ,3a1 a2

3. Упростить:

а)

i , j k

j,i k

k , i j k

;

б)

2i , j, k

3 j, i , k

4k , i , j

4. Найти площадь параллелограмма, построенного

векторах a и b :

а)

a (0; 1;1) ,

b (1;1;1) ;

; б)

на

б) a m 3n , b 3m n ,

1 , (m, n)

;

в) a m n , b 2m 2n ,

6 , (m, n)

Вычислить

площадь треугольника

вершинами

A(1, 1, 1), B(2, 3, 4) и С(4, 3, 2) .

5, (a,b) / 4 .

Вычислить

площадь

треугольника, построенного на векторах a 2b

и 3a 2b .

В треугольнике с вершинами А(1, 1, 2) ,

В (5, 6,2) и

С(1, 3, 1) найти высоту h

Вычислить

объем

тетраэдра

ОАВС,

если

OA 3i 9 j, OB 3 j k , OC 2i 5k .

9. Вычислить объем тетраэдра, заданного вершинами:

а)

А(0,0,0), B(1,1,0), C(2,1,0), D(0,0,6) ;

б)

А(0,0,0), B(4,1,1), C(1,1,0), D(0,0,8) .

10. Найти длину высоты параллелепипеда, построенного на

векторах		a i 5 j k , b 4i	2k , c i j k , если	за
основание взят параллелограмм,			построенный на векторах a	и
b .
11. Установить, компланарны ли векторы a, b, c , если
а) a 2,3, 1 , b 1, 1,3 , c 1, 9, 11 ;
б)	a 3, 2,1 , b 2,1, 2 , c 3, 1, 2 ;
в) a 3, 1, 2 , b 1, 2, 3 , c 3, 4, 7 .
12.	Установить, лежат ли		в одной плоскости точки
A(1, 2, 1), B 0,1,5 , C 1, 2,1 , D(2,1,3) .

II уровень

1. Найти площадь параллелограмма, построенного на

векторах	a p 2q	и b 2 p q , где p и q - единичные
векторы,	угол между которыми равен / 3.

Векторы a, b, c , образующие правую

тройку, взаимно

перпендикулярны.

Зная,

что

3 ,

вычислить

(a, b, c ) .

Вектор c перпендикулярен к векторам a и b , угол между

a и

b равен 300 . Зная,

что

3 , вычислить

(a, b, c ) .

Найдите

составляющую

вектора

a 1, 2,0 ,

перпендикулярную плоскости векторов e1 1,0,1		и e2 1,1,1 .
5. Даны три силы: F1 2, 1, 3 ,	F2 3, 2, 1 ,		F3 4,1,3
приложенные к точке A 1, 4, 2 .	Определить		величину и

направляющие косинусы момента равнодействующей этих сил относительно точки O 2,3, 1 .

Задания для самостоятельного решения

1. Найти вектор c , ортогональный векторам a (2, 3,1) и

b(1, 2,3) и удовлетворяющий условию (c, i 2 j 7k ) 10 .

2.Дан треугольник с вершинами


A(2, 1, 2),			B (1, 2, 1),	C 3, 2, 1 . Найти его площадь.
3.	Вычислить объем тетраэдра, вершины которого находятся
в точках A(2, 1, 1), B 5, 5, 4 , C 3, 2, 1 и D(4, 1, 3) .
4. Даны вершины тетраэдра
A(2,3,1),		B 4,1, 2 , C 6,3,7 , D( 5, 4,8) .						Найти его
высоту, опущенную из вершины D.
5.	Дана	сила F (2,		2, 9)	и точка ее			приложения
А (4,2, 3) . Вычислите величину						M	момента M этой силы
А (4,2, 3) . Вычислите величину						M	момента M этой силы
относительно точки O (2, 4, 0) .
относительно точки O (2, 4, 0) .

n 0 .

Ответы. 1. c (7,5,1) . 2. 22 . 3. 3. 4. 11. 5. 28.

2.4. Базис в n-мерном пространстве. Разложение векторов по базису.

Матрица перехода от одного базиса к другому


Упорядоченный		набор	n	действительных	чисел
x (x1, x2 ,	, xn ) называется		n-мерным вектором, а		числа
xi , i 1,	, n – компонентами вектора x .

Множество всех n-мерных векторов с введенными операциями сложения и умножения на число называется


векторным пространством Rn .
Система векторов x , x ,	, x	векторного пространства Rn
1 2	n
называется линейно независимой, если равенство
1 x1 2 x2	n xn 0 .		(2.12)

справедливо тогда и только тогда, когда 1 2 В противном случае эти векторы называются линейнозависимыми. Для того чтобы векторы x1 , x2 , , xn были линейнозависимыми, необходимо и достаточно, чтобы хотя бы один из них можно было представить в виде линейной комбинации остальных.

Рангом системы векторов называется максимальное число линейно независимых векторов данной системы. Ранг системы векторов равен рангу матрицы, составленной из компонент векторов системы.

Ранг векторного пространства Rn называется размерностью пространства и равен n.

Базисом системы векторов называется упорядоченная совокупность r линейно независимых векторов данной системы, где r – ранг системы.

Пусть e1,e2 , ,er – базис системы векторов. Каждый вектор

x данной системы можно представить и притом единственным образом в виде линейной комбинации векторов базиса:

x x1e1 x2e2	xr er .	(2.13)
Равенство (2.4.2) называется	разложением вектора	x по
базису e1,e2 , ,er , а числа x1 , x2 ,	, xr – координатами вектора
x в данном базисе.

Совокупность базисных векторов и их общего начала образует аффинную систему координат в пространстве.

Координаты векторов в таком случае называют аффинными. В случае, когда базисные векторы попарно перпендикулярны, то система координат называется прямоугольной декартовой системой координат.

В физическом пространстве R3 линейная независимость векторов равносильна их некомпланарности. Таким образом, любая тройка ненулевых некомпланарных векторов, взятых в определенном порядке, образует базис этого пространства.

Векторы

e1 1,0,0 , e2

0,1,0 , e3 0,0,1

образуют

стандартный ортонормированный базис в R3 .

Пусть

в линейном

пространстве

Rn заданы два базиса:

e e1 , e2 ,

, en

и e e1 , e2 ,

, en . Разложим векторы базиса

e по базису e:

2 j

... t

e ,

j 1,2,

, n .

1 j

		t	t	...	t
		11	12		1n
Матрицу	T	t21	t22	...	t2n ,	столбцы которой
	e e	... ...		...	...
		... ...		...	...

		tn1	tn2	...	tnn
являются координатами векторов базиса е						в базисе e, называют

матрицей перехода от базиса e к базису е .

Свойства матрицы перехода:

1. Матрица перехода от одного базиса n-мерного линейного пространства Rn к другому его базису является невырожденной матрицей n-го порядка.

2. Любая невырожденная квадратная матрица n-го порядка служит матрицей перехода от одного базиса n-мерного

линейного пространства

к некоторому

другому

базису

пространства Rn .

3. Пусть

имеются три базиса e, f , g пространства Rn

известны матрицы перехода Te f

от базиса e

к базису f

и Tf g

от базиса f к базису g . Тогда

Te g

Te f Tf g .

(2.14)

4. Если Te f – матрица перехода от базиса e

к базису f , то

матрица Te f

обратима и обратная матрица является матрицей

перехода от

базиса f к

базису

e :

T 1

. Координаты

f e

e f

вектора v в базисах e и f

связаны формулами:

T 1

(2.15)

e f

f e

e f

где ve , vf

− вектор-столбцы координат вектора v в базисах

e и f соответственно.

Если векторы

базисов

заданы

координатами

некотором базисе е0 , то матрица перехода от базиса e к базису

е находится по формуле
T	T	0	T 0	e	T 01 T 0	e	,	(2.16)
e e	e e		e	e	e e e	e

Пример 1. Показать,	что векторы a 2, 0,1 , b 1, 1,1 ,
c 1, 1,2 образуют	базис, и найти координаты вектора

d 3, 1,1 в этом базисе.

Решение. 1-й способ. В трехмерном пространстве базис образуют любые три линейно-независимых ненулевых вектора.

Составим линейную комбинацию векторов a,b , c с коэффи-

циентами , , R и приравняем к нулевому вектору 0 :

a b c 0 .

Полученное равенство запишем в координатной форме

2, 0,1 1, 1,1 1, 1, 2 0, 0,0 .

Из определения равенства двух векторов имеем систему

2 0,
	0,

2 0,

решая которую получим: 0 . Следовательно a,b , c – линейно-независимые векторы (образуют базис).

Найдем в этом базисе координаты вектора				d	(разложим
вектор d по базису) d d1a d2b d3c	или в координатной
форме d1 2,0,1 d2 1, 1,1 d3 1, 1, 2 3, 1,1 .
	2d1 d2 d3 3,
Получим систему линейных уравнений		d2	d3		1,

	d	d	2	2d		3	1.
	1
Решая последнюю систему, получим	d1 1, d2 2, d3 1 .
Следовательно d a 2b c , т. е. в базисе a,b , c					вектор d
имеет координаты: d 1, 2, 1 .

2-й способ. Найдем матрицу перехода от стандартного базиса

e (1,0,0), e		(0,1,0), e	(0,0,1) трехмерного пространства R3
1	2	3

к системе векторов a,b , c .

	2		1	1
T		0	1	1 .
e a
		1	1	2
		1	1	2

Так как определитель матрицы перехода
											1	1
										2	1	1
						Te a				0	1 1		2 1 1 0 2
						Te a				0	1 1		2 1 1 0 2
										1	1	2
не		равен				0,			то		матрица Te a					невырожденная			и,
следовательно,						a,b , c является базисом.
Найдем координаты вектора d														в базисе a,b , c
							2 1				1 1			3		1 1	0	3		1
d		T	1	d				0	1		1			1	1	1 3 2		1		2	.
d		T		d				0	1		1			1		1 3 2		1		2	.
	a	e a			e										2
								1 1			2			1	2	1 1 2		1
								1 1			2			1		1 1 2		1		1

Таким образом d a 2b c .

Пример

Разложить

вектор

S a b c

по трем

некомпланарным векторам:

p a b,

q a b,

r 2b 3c .

Решение. Пусть S p q r , где , , R . Тогда

a b c a b a b 2b 3c

a 2 b 3 c

Приравнивая

коэффициенты справа

и слева

получим

систему:

решая

которую,

получим

2 1,

3 1,

. Следовательно S

r .

<<< < Предыдущая 1 2 3 4 5 67 / 137 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.2019500.74 Кб2Metodicheskie_ukazania_po_vypolneniyu_kursovoy_....doc
#
31.05.20151.73 Mб20metodichka . физика.pdf
#
31.05.2015597.5 Кб16metodichka по МП пассажиров.doc
#
05.12.20189.82 Mб20Metodichka.doc
#
26.03.20161.61 Mб51MetodichkaC_14ch1.doc
#
26.03.20162.68 Mб20metodichkaFTUG_chast1.pdf
#
26.03.20161.82 Mб6metodichkaFTUG_chast2.pdf
#
10.11.20197.85 Mб10Metodichka_1_kurs.doc
#
26.03.201685.22 Кб12metodichka_magistranty.docx
#
31.05.20151.09 Mб4Metodichka_ME_i_VED.doc
#
20.12.2018310.78 Кб5metodichka_mido-progr.doc