
metodichkaFTUG_chast1
.pdf
2) |
x 1 t, y 2 3t, z 1 5t.5.1) 3; 2) 25. 6.1) 60°;2) 90°. 7. |
127 |
. |
||||||||||||||||||
13 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8. |
x 2 |
|
y 1 |
|
|
z 3 |
|
. 9. x 3 3t, y 1 15t, |
z 3 19t; |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
6 |
|
|
|
1 |
|
7 |
|
|
|
|||||||||||
|
3.4. Взаимное расположение прямой и плоскости в |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пространстве |
|
|
|
||
|
Пусть прямая L задана каноническими уравнениями: |
|
|
||||||||||||||||||
|
L : |
x x0 |
|
|
y y0 |
|
|
z z0 |
, |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
l |
|
|
|
|
m |
|
|
|
|
n |
|
|
|
|||||
|
|
|
|
||||||||||||||||||
где M0 (x0 , y0 , z0 ) L, |
a (l, m, n) || L, а плоскость P задана общим |
||||||||||||||||||||
уравнением: P : Ax By Cz D 0, где n ( A, B, C) P.
Тогда взаимное расположение прямой L и плоскости P в пространстве можно определить по взаимному расположению
направляющего вектора a прямой L и нормального вектора n плоскости P.
Взаимное расположение прямой L и плоскости P в пространстве:
1)Прямая L параллельна плоскости P :
|
|
|
|
|
Al Bm Cn 0, |
|||||
|
|
|
|
|
||||||
L || P a n, M0 |
|
|
|
|
|
|
||||
P |
|
By |
Cz |
|
(3.27) |
|||||
|
|
|
|
|
Ax |
0 |
0. |
|||
|
|
|
|
|
|
0 |
0 |
|
|
|
2)Прямая L принадлежит плоскости P :
|
|
|
|
|
|
|
|
Al Bm Cn 0, |
|
||
|
|
|
|
|
|
||||||
a n, |
|
|
|
(3.28) |
|||||||
L P |
|
P |
|
|
By0 Cz0 |
0. |
|||||
M |
0 |
Ax0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|||
3)Прямая L и плоскость P пересекаются:
|
|
|
|
|
|
|
|
|
|
L P M1 a n Al Bm Cn 0. |
(3.29) |
||||||||
|
|
|
|
|
|
||||
L P a || n. |
(3.30) |
||||||||
Угол между прямой и плоскостью:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
(a, n) |
|
|
|
Al Bm Cn |
|
|
.(3.31) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
cos(a, n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
a |
n |
|
|
l2 m2 n2 |
|
A2 B2 C2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Пример 1. Установить |
взаимное расположение |
прямой и |
|||||||||||||||||||||||||
101

|
|
|
|
|
|
x 2 3t, |
|
|||||||
плоскости: 1) y 1 4t, |
и |
4x 3y 6z 5 0; |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
z 5 4t. |
|
|||||||
2) |
x 13 |
|
|
y 1 |
|
|
z 4 |
|
и |
x 2y 4z 1 0; |
||||
|
|
|
|
|
|
|
||||||||
|
|
8 |
|
|
|
2 |
|
|
|
|
3 |
|
|
|
3) |
x |
|
y 1 |
|
z 1 |
|
и 5x 7y 13z 13 0. |
|||||||
|
|
3 |
||||||||||||
|
1 |
4 |
|
|
|
|
|
|
||||||
Решение. 1) Координаты направляющего вектора прямой
|
|
|
|
M0 ( 2,1, 5) , принадлежащей |
|
a (3, -4, 4), координаты точки |
|||
|
|
|
|
|
прямой. Нормальный вектор n |
плоскости имеет координаты |
|||
n (4, 3, 6). Найдем скалярное произведение векторов a и n : a, n 3 4 4 (3) 4 6 12 12 24 0.
Значит, a n, т. е. прямая L и плоскость P параллельны. Проверим, не лежит ли прямая L в плоскости P. Для этого определим, принадлежит ли плоскости P точка M0 . Подставим ее координаты в уравнение плоскости: 4 2 31 6 5 5 0.
Таким образом, выполняются условия (3.27), следовательно,
M0 P, а значит, L || P. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
2) Прямая L : |
x 13 |
|
|
y 1 |
|
|
z 4 |
|
|
имеет направляющий вектор |
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
8 |
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
a (8, |
2, 3) и проходит через точку M0 |
(13, 1, |
4). |
Нормальный |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
вектор n плоскости имеет координаты |
n (1, |
2, |
4) . |
Найдем |
|||||||||||||||||||||||||
скалярное произведение: |
|
, |
|
81 2 2 3 (4) 8 4 12 0. |
|||||||||||||||||||||||||
a |
n |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
Так как оно равно нулю, то a n. |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
Проверим принадлежность точки M0 |
плоскости: |
|
||||||||||||||||||||||||
13 2 1 4 4 1 13 2 16 1 0. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
Значит, прямая L лежит в плоскости P. |
|
|
|
|
|
|||||||||||||||||||||
3) |
|
|
Координаты |
|
направляющего |
|
вектора |
прямой |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
a (1, |
4, -3). Нормальный |
|
вектор |
n |
|
плоскости |
имеет |
|||||||||||||||||||||
102
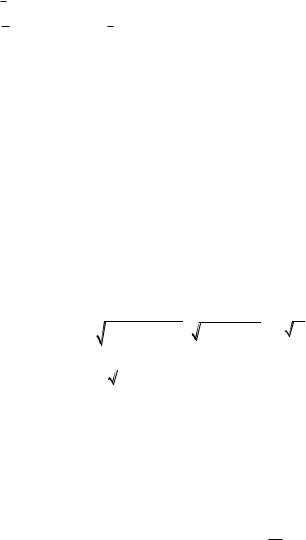
координаты n (5, 7, 13).
Векторы a (1, 4, -3) и n (5, 7, 13) не коллинеарны и не
перпендикулярны, так как |
1 |
|
|
4 |
|
3 |
(коэффициенты не |
|
5 |
7 |
13 |
||||||
|
|
|
|
|||||
пропорциональны) и 15 4 7 3 13 5 28 26 7 0 (скалярное произведение не равно нулю). Значит, L P M1.
Пример 2. Определить угол между прямой L и плоскостью P, найти их точку пересечения :
|
|
L : |
x 8 |
|
|
y 7 |
|
z 11 |
, P : 4x y 3z 5 0. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
3 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Решение. |
|
|
|
Координаты |
направляющего |
|
вектора |
прямой |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
a (3, 2, 1). |
|
Нормальный |
вектор |
|
n |
|
плоскости |
имеет |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
координаты n (4, 1, |
3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
По формуле (3.31) получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 4 2 |
1 1 3 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(a, n) |
|
|
|
|
|
|
|
|
13 |
|
|||||||||||||||||||||||
|
|
sin |
cos(a, n) |
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
n |
|
|
|
2 |
|
|
2 |
2 |
|
|
|
|
|
2 |
2 2 |
|
2 91 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 2 |
1 |
|
4 |
|
1 3 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arcsin |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Таким образом (L, P) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
91 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем координаты точки М1 пересечения прямой и плоскости. Составим параметрические уравнения прямой:
x 8 3t,y 7 2t,
z 11 t.
Подставим выражения для x, y, z в уравнение плоскости:
4(8 3t) (7 2t) 3(11 t) 5 0 13t 67 0 или t 1367 .
Подставив найденное значение параметра t в параметрические уравнения прямой, найдем координаты точки
пересечения: |
x 8 3 |
|
|
67 |
|
|
97 |
, |
y 7 2 |
|
|
67 |
|
|
225 |
, |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|||||||||||||
|
|
|
|
13 |
|
|
13 |
|
|
|
|
13 |
|
|
13 |
|
103
z 11 1367 1376 .
Получили |
точку M ( |
97 |
|
, |
225 |
, |
76 |
), |
в которой |
прямая |
|||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
1 |
13 |
|
13 |
|
13 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
пересекает плоскость. |
|
|
|
|
|
|
|
|
|
|
|||||||
Пример |
3. |
Найти |
|
уравнения |
проекции |
прямой |
|||||||||||
L : |
x 4 |
|
y 1 |
|
z |
на плоскость |
|
P : x 3y z 8 0 . |
|
||||||||
|
2 |
|
|
|
|
||||||||||||
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||||
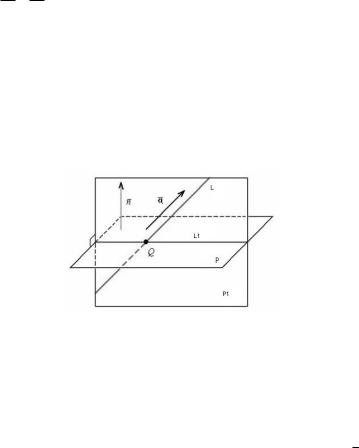
Решение. |
Найдём |
уравнение |
|
плоскости P , |
которая |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
перпендикулярна плоскости P и проходит через прямую L .
Рис. 3.1
Уравнение |
плоскости P можно |
составить по |
любой |
|||
|
1 |
|
|
|
||
точке, которая принадлежит прямой |
L , направляющему |
|||||
вектору прямой L и вектору нормали плоскости P . |
|
|||||
Из равнений прямой |
L |
получаем координаты |
||||
|
|
|
|
|
|
|
направляющего |
вектора a (3, |
2, 4), координаты |
точки |
|||
M0 (4, 1, 0) , принадлежащей прямой L . Нормальный вектор n
|
|
|
|
|
|
|
||
плоскости P имеет координаты n (1, |
3, |
1). |
||||||
Составим уравнение |
плоскости |
P , |
воспользовавшись |
|||||
|
|
|
|
|
|
|
1 |
|
|
x 4 |
y 1 |
z |
|
|
|
||
|
|
|
|
|||||
формулой (3.11): |
3 |
2 |
4 |
0. |
|
|
||
|
1 |
3 |
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
Преобразуем левую часть:
104

x 4 |
y 1 |
|
|
|
|
|
|
|
|
|
|
|
z |
|
2 |
4 |
|
3 |
4 |
|
3 |
2 |
|
||
3 |
2 |
4 |
(x 4) |
(y 1) |
z |
(x 4)(2 12) |
||||||
1 |
3 |
1 |
|
3 |
1 |
|
1 |
1 |
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|||
(y 1)(3 4) z(9 2) 14(x 4) 7(y 1) 7z.
Таким образом, получаем общее уравнение искомой плоскости 2x y z 7 0.
На Рис. 3.1 видно, что проекцией прямой L на плоскость P является прямая L1 , которую можем найти как пересечение
плоскостей P
плоскость P :
и P . Таким образом проекция прямой L |
на |
|
|
1 |
|
|
x 3y z 8 0, |
|
L1 |
: |
|
|
2x y z 7 0. |
|
Задания для самостоятельного решения I уровень
1.1. Найдите точку пересечения прямой L с плоскостью P или установите их параллельность:
x 2 3t,
1)L : y 1 4t, P : 4x 3y 6z 5 0;
z 5 4t,
2) L : |
x 1 |
|
y 3 |
|
z 2 |
, P : x y 2z 2 0; |
|
|
|
|
|
||||
|
1 |
|
7 |
2 |
|
||
1.2. Найдите угол между прямой и плоскостью:
x 2 t,
1) y 5 2t, и 3x y 5z 7 0;
z 3 t
2) |
x 3 |
|
y |
|
z 1 |
|
и x 2y z 10 0; |
||
|
|
|
|
|
|||||
4 |
|
1 |
1 |
||||||
|
|
|
|
|
|||||
5x 3y 2z 5 0,
1.3. Доказать, что прямая лежит в
2x y z 1 0.
плоскости 4x 3y 7z 7 0.
II уровень
105
2.1. При каком значении |
m прямая |
x 1 |
|
y 2 |
|
z 3 |
|
|
|
2 |
|||||
|
3 |
|
m |
|
|||
параллельна плоскости x 3y 6z 7 0, найти расстояние от прямой до плоскости.
x 3 4t,
2.2. При каких значениях А и D прямая y 1 t,
z 3 t.
лежит в плоскости Ax 2y 4z D 0.
2.3. Составить уравнение плоскости, проходящей через две
параллельные прямые |
|
|
|
|
|
|
|
|
|
|
||||
|
x 2 |
|
y 1 |
|
|
z 3 |
, |
x 1 |
|
y 2 |
|
z 3 |
. |
|
|
|
|
2 |
|
|
|
|
|||||||
3 |
2 |
|
|
|
3 |
|
2 |
|
2 |
|||||
2.4. При каких значениях А и В плоскость
x 3 2t,
Ax By 3z 5 0 перпендикулярна к прямой y 5 3t,
z 2 2t.
|
|
|
x y z 2 0, |
|
2.5. Найти |
угол между |
прямой |
|
и |
|
|
|
2x y z 1 0. |
|
плоскостью, |
проходящей |
через |
точки |
A(2, 3, -1) , |
B(1, 1, 0), C(0, -2, 1) .
2.6. Составить канонические уравнения прямой, проходящей через точку М0 (2; -4; -1) и середину отрезка прямой
3x 4y 5z 26 0,
заключённого между плоскостями:
3x 3y 2z 5 0,
5x 3y 4z 11 0 и 5x 3y 4z 41 0 .
2.7.Составьте уравнение прямой, проходящей через точку A(1, 2, 1) и перпендикулярной плоскости 3x 7 y 2z 5 0.
2.8.Напишите уравнение плоскости, проходящей через точку
106
A(1, 2, 2) перпендикулярно прямой |
x 3 |
|
y 6 |
|
z 3 |
. |
|
|
|
3 |
|
||||
|
4 |
|
|
2 |
|
||
2.9. Составить уравнение плоскости, проходящей через точку
M (1, 2, 1) |
x 2 y z 3 0, |
|
перпендикулярно к прямой |
|
|
|
x y z 2 |
0. |
2.10. Составить уравнение плоскости, проходящей через
точку M (1, |
2, 1) параллельно прямым |
|
|
|
|
|
|
|||||||||
|
x 1 |
|
y 1 |
|
|
z 1 |
, |
|
x 5 |
|
y 2 |
|
z 3 |
. |
||
|
2 |
|
|
|
3 |
|
|
3 |
|
|
3 |
|
2 |
|
1 |
|
2.11. Составить уравнение плоскости, проходящей через
x 1 3t,
прямую y 3 2t,
z 2 t.
2x y z 3 0,
параллельно прямой
x 2 y z 5 0.
2.12. Составить канонические уравнения прямой, которая
проходит через точку M (3, 2, -4) |
параллельно |
плоскости |
|||||||||||
3x 2y 3z 7 0 и пересекает прямую |
|
x 2 |
|
y 4 |
|
z 1 |
. |
||||||
|
|
2 |
|
||||||||||
|
|
|
|
|
3 |
|
|
|
2 |
|
|||
2.13. Найти проекцию точки M (5, 2, -1) на плоскость |
|||||||||||||
2x y 3z 23 0 . |
|
|
|
|
|
|
|
|
|
|
|
||
2.14. |
Найдите |
точку, симметричную |
точке A(6, 5, 5) |
||||||||||
относительно плоскости 2x 3y z 4 0. |
|
|
|
|
|
|
|
||||||
2.15. |
Найдите |
проекцию |
прямой |
L |
|
на |
плоскость |
||||||
3x 2y z 15 0, если она задана уравнениями: |
|
|
|
|
|
||||||||
x 1 2t, |
|
x y z 5 0, |
|
|
|
||||||||
|
3 |
t, |
2) |
|
|
|
|||||||
1) y |
|
|
|
|
|
0. |
|
|
|
||||
|
2 |
t; |
|
2x 3y z 4 |
|
|
|
||||||
x |
|
|
|
|
|
|
|
|
|
|
|
||
Задания для самостоятельного решения
107
3x 2 y z 3 0
1. При каком значении С прямая
4x 3y 4z 1 0
параллельна плоскости 2x y Cz 2 0.
|
x 1 |
|
y 2 |
|
z 5 |
x 7 3t, |
|
|
|
|
|
||||
2. Доказать, что прямые |
|
|
|
|
и y 2 2t, |
||
2 |
|
3 |
4 |
||||
|
|
|
|
|
|||
|
|
|
|
|
|
|
z 1 2t. |
лежат в одной плоскости, и составить уравнение этой плоскости.
3. Установить взаимное расположение прямой и плоскости. В случае их пересечения найти координаты точки пересечения:
1) |
|
x 1 |
|
|
y 1 |
|
z |
, 2x 3y z 1 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
2 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2) |
|
x 3 |
|
y 2 |
|
|
|
|
z 1 |
, |
|
x 2 y z 15 0 ; |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
3) |
|
|
x 2 |
|
y 1 |
|
|
z 3 |
, |
|
x 2 y 2z 6 0 . |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
4. |
При каких значениях t и С прямая |
x 2 |
|
|
y 1 |
|
|
|
z 5 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
4 |
|
|
|
|
||||||
перпендикулярна к плоскости 3x 2y Cz 1 0 . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
5. |
Составить уравнения прямой, проходящей через точки |
|||||||||||||||||||||||||||||||||||||||||||||
пересечения плоскости x 3y 2z 1 0 с прямыми |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
x 5 |
|
y 1 |
|
z 3 |
и |
x 3 |
|
|
y 4 |
|
z 5 |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
5 |
|
|
|
2 |
|
1 |
4 |
|
|
|
6 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
6. |
Составить уравнения прямой, проходящей через точку |
|||||||||||||||||||||||||||||||||||||||||||||
M(2, 3, -5) перпендикулярно к плоскости |
6x 3y 5z 2 0. |
|||||||||||||||||||||||||||||||||||||||||||||
7. |
Напишите уравнение плоскости, проходящей через точку |
|||||||||||||||||||||||||||||||||||||||||||||
M (1, |
|
1, 1) |
перпендикулярно прямой |
|
x 3 |
|
y 1 |
|
|
z 2 |
. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
4 |
|
|
|||||||
8. |
|
|
Составить |
уравнение плоскости, |
проходящей через |
|||||||||||||||||||||||||||||||||||||||||
108
x 1 2t,
прямую y 2 3t, и точку M (2, 2, 1) .
z 3 2t.
9. Составить уравнение плоскости, проходящей через
прямую |
x 1 |
|
y 2 |
|
z 2 |
перпендикулярно к плоскости |
|
|
|
3 |
|
||||
|
2 |
|
|
2 |
|
||
3x 2y z 5 0.
10. Найти проекцию точки M (3, 4, -2) на плоскость, проходящую через параллельные прямые
|
|
|
x 5 |
|
y 6 |
|
z 3 |
, |
|
|
x 2 |
|
y 3 |
|
|
z 3 |
. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|||||||||||||
|
|
13 |
|
|
|
|
1 |
|
|
|
|
|
13 |
|
1 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
11. Найти точку Q, симметричную |
точке |
P(3, 4, -6) |
||||||||||||||||||||||||||||||
относительно |
|
плоскости, |
проходящей через |
M1 ( 6, 1, -5) , |
||||||||||||||||||||||||||||||
M2 |
(7, |
2, -1) , |
|
M3 (10, 7, 1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Ответы. |
1. С = — 2. 2. |
2x 16y 13z 31 0. 3. |
1) |
|||||||||||||||||||||||||||||
(2, |
3, 6); |
|
2) прямая параллельна плоскости; 3) прямая лежит на |
|||||||||||||||||||||||||||||||
плоскости. |
4. |
|
t 6 , С |
= |
|
3 |
. |
5. |
|
x 1 |
|
y 2 |
|
z 3 |
. |
6. |
||||||||||||||||||
|
|
|
|
|
1 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
7 |
|
|
|
|
5 |
|
|||||||
|
x 2 |
|
|
y 3 |
|
|
z 5 |
. 7. |
2x 3y 4z 1 0. |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
6 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
8. 4x 6y 5z 1 0. 9. x 8y 13z 9 0. 10. (2, |
3, -5) . 11. |
Q |
||||||||||||||||||||||||||||||||
(1; 2; —2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
3.5. Кривые второго порядка на плоскости |
|
||||||||||||||||||||||
Линией (кривой) второго порядка называется множество М,
общее уравнение которой в декартовой прямоугольной системе координат имеет вид:
Ax2 By2 2Cxy 2Dx 2Ey F 0, |
(3.32) |
где коэффициенты при одночленах второй степени одновременно не равны нулю.
Рассмотрим частные случаи:
109

1) Эллипс |
x2 |
|
y2 |
1. |
|
a2 |
b2 |
||||
|
|
|
Рис. 3.2
2) Гипербола |
x2 |
|
y2 |
1 . |
|
a2 |
b2 |
||||
|
|
|
Рис. 3.3
3) Парабола y2 2 px .
Рис. 3.4
Пример 1. Записать каноническое уравнение эллипса, проходящего через точки M (0,7), N(4, 1) . Найти полуоси, фокусы и эксцентриситет.
110
