
- •Методические рекомендации по выполнению лабораторных работ
- •664074, Иркутск, ул. Лермонтова, 83 содержание
- •Лабораторная работа 1-1 Физические измерения и обработка результатов
- •Порядок выполнения работы Определение ускорение свободного падения с помощью математического маятника.
- •Основные определения теории приближенных вычислений
- •Правила действий над приближенными числами
- •Приложение 1.3 Графическое представление результатов опыта
- •Приложение 1.4 Значение параметра Стьюдента в зависимости от вероятности и числа степеней свободы.
- •Приложение 1.5
- •Литература
- •Лабораторная работа 1-2 изучение кинематики и динамики поступательного движения на машине атвуда
- •Порядок выполнения работы
- •Задание 1. Проверка закона скоростей
- •Задание 2. Проверка закона перемещений
- •Задание 3. Проверка второго закона Ньютона.
- •Метод наименьших квадратов
- •Контрольные вопросы
- •Литература
- •Лабораторная работа 1-3 Механические колебАния
- •Контрольные вопросы
- •Литература
- •Лабораторная работа 1-4 Определение момента инерции и проверка закона сохранения энергии с помощью маятника Максвелла
- •Контрольные вопросы
- •Главные оси тензора инерции
- •Нахождение главных осей
- •Моменты инерции относительно осей
- •Описание эксперимента
- •Контрольные вопросы
- •Литература
- •Цель работы: изучить виды деформации твердого тела и определить модули сдвига исследуемого материала. Теоретическая часть Деформация
- •Закон Гука
- •Всестороннее сжатие
- •Чистый сдвиг
- •Чистое кручение
- •Чистое кручение при деформации цилиндрической пружины
- •Экспериментальная часть Приборы и принадлежности: цилиндрические пружины из исследуемых материалов, набор грузиков, прибор для измерения периодов колебаний.
- •Порядок выполнения работы
- •Контрольные вопрсы
- •Экспериментальная часть
- •Определение угловой скорости маятника
- •Определение момента инерции маятника
- •Порядок выполнения работы
- •Описание экспериментальной установки
- •Контрольные вопросы
- •Литература
- •Правила безопасности труда
- •Лабораторная работа 1-9 изучение прецессии гироскопа
- •Время непрерывной работы двигателя гироскопа – 10 минут, перерыв 5 минут.
- •Контрольные вопросы
- •Литература
Нахождение главных осей
Главные оси во
многих случаях могут быть найдены без
громоздких математических расчетов,
которые надо провести для диагонализации
тензора инерции. Для этого иногда бывает
достаточно воспользоваться простыми
соображениями симметрии. Пусть имеется
плоская пластинка бесконечно малой
толщины. Точка, через которую проходят
главные оси, лежит на пластинке. Направим
ось
![]() перпендикулярно ей. Очевидно, что
координаты
перпендикулярно ей. Очевидно, что
координаты![]() всех точек пластинки равны нулю, т.е.
все
всех точек пластинки равны нулю, т.е.
все![]() .
В этом случае из формулы (3) имеем
.
В этом случае из формулы (3) имеем![]() .
Следовательно, любая ось, перпендикулярная
этой пластинке, будет главной. Две другие
главные оси расположены в плоскости
пластинки взаимно перпендикулярно друг
другу. Их направление зависит от формы
пластинки.
.
Следовательно, любая ось, перпендикулярная
этой пластинке, будет главной. Две другие
главные оси расположены в плоскости
пластинки взаимно перпендикулярно друг
другу. Их направление зависит от формы
пластинки.
Р ассмотрим
случай круглой пластинки (рис.3) конечной
толщины. Точка
ассмотрим
случай круглой пластинки (рис.3) конечной
толщины. Точка![]() ,
лежащая в средней плоскости пластинки,
есть точка, относительно которой надо
найти главные оси. Очевидно, что одна
главная ось направлена перпендикулярно
плоскости пластинки. Утверждается, что
другой главной осью является ось, лежащая
в средней плоскости и проходящая через
эту точку и центр диска. Эта ось на рис.3
взята за ось
,
лежащая в средней плоскости пластинки,
есть точка, относительно которой надо
найти главные оси. Очевидно, что одна
главная ось направлена перпендикулярно
плоскости пластинки. Утверждается, что
другой главной осью является ось, лежащая
в средней плоскости и проходящая через
эту точку и центр диска. Эта ось на рис.3
взята за ось![]() .
Убедимся в этом. Имеем:
.
Убедимся в этом. Имеем:
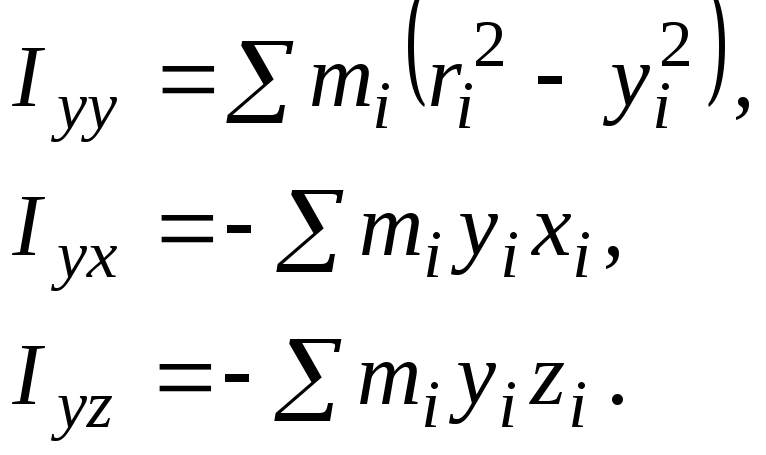
Видно, что
![]() и
и![]() из-за симметрии пластинки относительно
плоскостей
из-за симметрии пластинки относительно
плоскостей![]() и
и![]() .
Таким образом, выбранная ось действительно
является главной. Третья главная ось
однозначно определяется двумя найденными,
будучи перпендикулярной им обеим.
Проверим, что ось
.
Таким образом, выбранная ось действительно
является главной. Третья главная ось
однозначно определяется двумя найденными,
будучи перпендикулярной им обеим.
Проверим, что ось![]() действительно является главной. Имеем:
действительно является главной. Имеем:
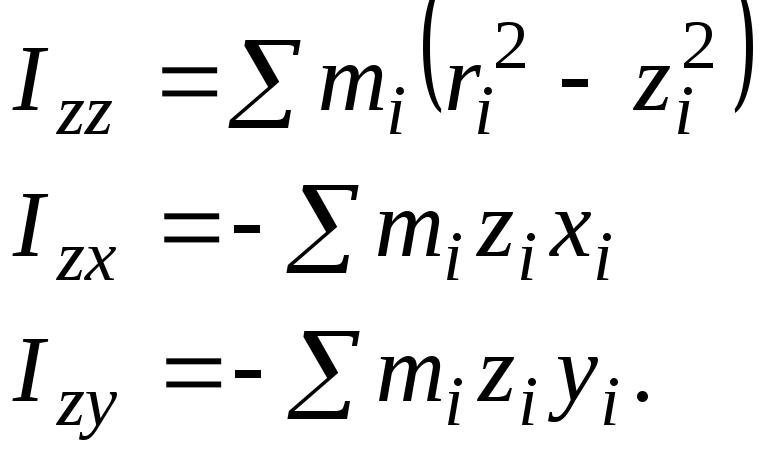 (7)
(7)
Равенства
![]() обусловливаются симметрией пластинки
относительно плоскости
обусловливаются симметрией пластинки
относительно плоскости![]() .
.
Если круглая пластинка имеет значительную толщину, то она называется круглым цилиндром. Все изложенные о главных осях пластинки соображения остаются, конечно, справедливыми и для цилиндра.
Моменты инерции относительно осей
Известно, что момент импульса относительно оси, проходящей через центр масс, можно записать так:
![]() , (8)
, (8)
где![]() - тензор момента инерции относительно
системы координат, начало которой
совпадает с центром масс. Компоненты
- тензор момента инерции относительно
системы координат, начало которой
совпадает с центром масс. Компоненты![]() будут постоянны во времени, если система
координат неизменно связана с телом.
будут постоянны во времени, если система
координат неизменно связана с телом.
Зная
![]() ,
можно найти момент инерции относительно
любой оси, проходящей через
,
можно найти момент инерции относительно
любой оси, проходящей через![]() - центр масс тела. Пусть направление оси
вращения задано вектором
- центр масс тела. Пусть направление оси
вращения задано вектором![]() .
Тогда, учитывая, что
.
Тогда, учитывая, что![]() ,
по формуле (8) проекцию
,
по формуле (8) проекцию![]() на
на![]() можно записать так:
можно записать так:![]() ,
где
,
где![]() - момент инерции относительно оси
- момент инерции относительно оси![]() .
Или:
.
Или:![]() .
Если записать число
.
Если записать число![]() через компоненты тензораI0
и вектора
через компоненты тензораI0
и вектора![]() ,
то получим довольно громоздкое выражение.
Приведем более краткую и ясную формулу,
приняв за оси координат главные
направления
,
то получим довольно громоздкое выражение.
Приведем более краткую и ясную формулу,
приняв за оси координат главные
направления![]() ;
тогда
;
тогда![]() ,
где
,
где![]() – направляющие косинусы
– направляющие косинусы![]() по отношению к осям
по отношению к осям![]() .
Следовательно:
.
Следовательно:
![]() .
.
Поэтому:
![]() .(9)
.(9)
г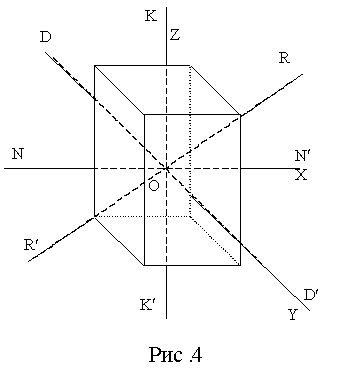 де
де![]() – моменты инерции относительно главных
осей, проходящих через центр масс. По
формуле (9) можем при известных
– моменты инерции относительно главных
осей, проходящих через центр масс. По
формуле (9) можем при известных![]() и
и![]() точно определить момент инерции
точно определить момент инерции![]() относительно любой оси
относительно любой оси![]() .
.
Описание эксперимента
Итак, для момента
инерции
![]() имеем формулу:
имеем формулу:
![]() , (10)
, (10)
где
![]() - направляющие косинусы;
- направляющие косинусы;![]() - моменты инерции относительно осей,
проходящих через середины противоположных
граней и через геометрический центр
прямой призмы – точку
- моменты инерции относительно осей,
проходящих через середины противоположных
граней и через геометрический центр
прямой призмы – точку![]() (оси
(оси![]() на рис.4), а
на рис.4), а![]() – момент инерции относительно диагональной
оси, проходящей через противоположные
вершины груза (ось
– момент инерции относительно диагональной
оси, проходящей через противоположные
вершины груза (ось![]() ).
).
Запишем выражение для уравнения колебаний физического маятника
![]() , (11)
, (11)
которое можно переписать в виде:
![]() , (11а)
, (11а)
где
![]() - момент инерции маятника, а
- момент инерции маятника, а![]() .
Выразим момент инерции
.
Выразим момент инерции![]() через период колебаний
через период колебаний![]() ,
т.е.
,
т.е.
![]() , (12)
, (12)
где ![]()
![]() (13)
(13)
Подставляя эти соотношения в формулу (10), получим:
![]() (14)
(14)
или
![]() (14а)
(14а)
Теперь рассмотрим
для примера образец в виде прямого
параллелепипеда с ребрами
![]() .
Для его диагонали квадраты
направляющих косинусов имеют вид:
.
Для его диагонали квадраты
направляющих косинусов имеют вид:
 (15)
(15)
Тогда выражение (14а) принимает вид:
![]() , (16)
, (16)
где
![]() .
.
Следовательно
![]() , (17)
, (17)
где левая часть
![]() ,
,
а правая часть
![]() .
.
И тогда соотношение (17) можно записать в виде:
![]() (18)
(18)
Таким образом, проверка выполнения соотношения для моментов инерции (10) сводится в эксперименте к проверке соблюдения соотношения для периодов колебаний(18), что и является задачей этой лабораторной работы.
Величины
![]() определяются экспериментально из 5
опытов.
определяются экспериментально из 5
опытов.
Для каждого периода колебаний вычисляются
![]()
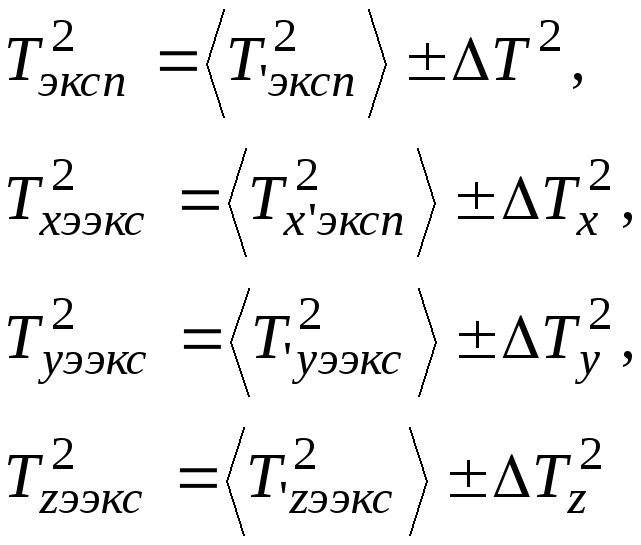
![]() определяется по
формуле:
определяется по
формуле:
![]() ,
где
,
где![]() – коэффициент Стьюдента.
– коэффициент Стьюдента.
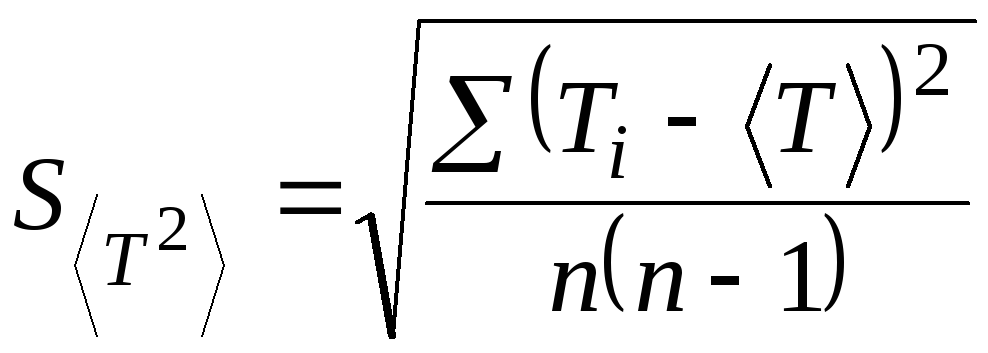 (19)
(19)
Затем рассчитывается
![]()
![]() определяется по
формуле
определяется по
формуле
![]() (20)
(20)
Для расчета
доверительного интервала находят
среднее квадратичное величины
![]()
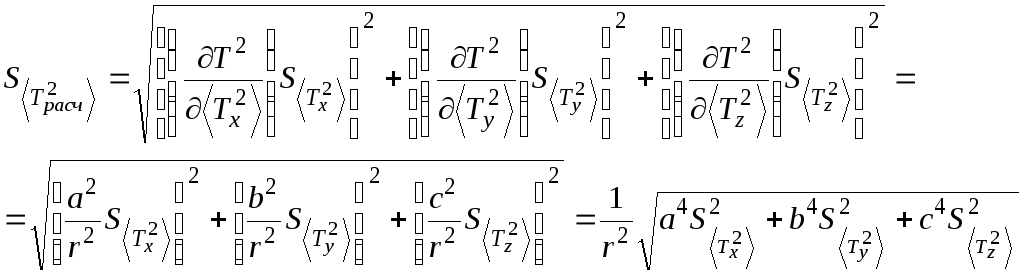
где
![]()
![]() (21)
(21)
где
![]() – коэффициент Стьюдента.
– коэффициент Стьюдента.
Порядок проведения работы
Задача работы: оценка моментов инерции твердых тел правильной геометрической формы методом крутильных колебаний.
Приборы и принадлежности: унифилярный подвес, набор образцов (тел правильной геометрической формы), штангенциркуль.
Подготовить прибор к работе, установить магнит в выбранном положении.
Измерить с помощью штангенциркуля геометрические размеры образца – длину, высоту и ширину
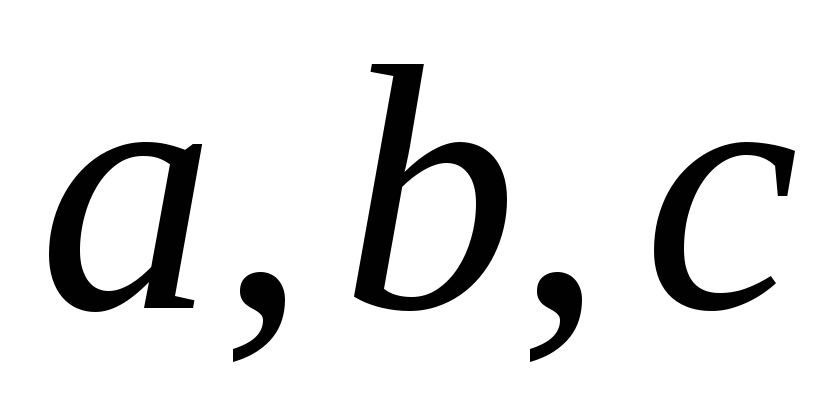 – в формуле (20).
– в формуле (20).В рамке прибора закрепить образец по оси, проходящей через центры противоположных граней (главная ось).
Поворачивая рамку прибора, приблизить ее стрелу к электромагниту таким образом, чтобы электромагнитная сила фиксировала положение рамки.
Нажать кнопку «Пуск».
После считывания измерителем не менее 10 крутильных колебаний, нажать кнопку «Стоп».
Вычислить период колебаний крутильного маятника по формуле
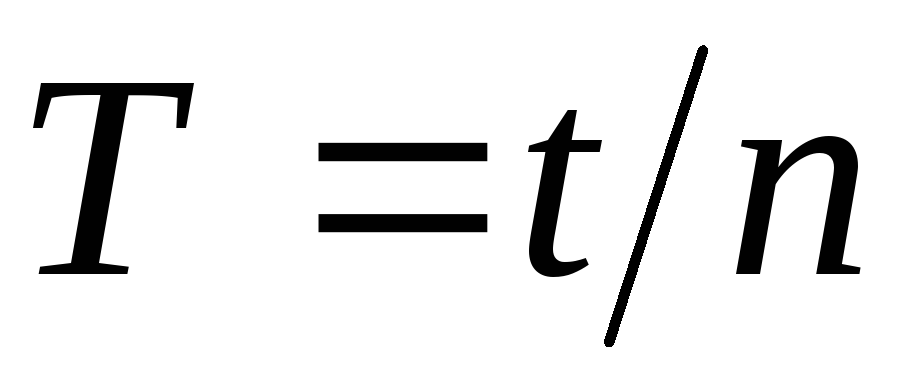 ,
где
,
где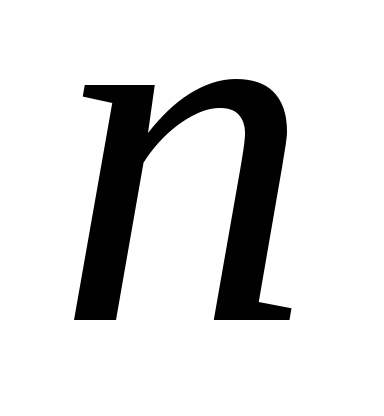 – число колебаний,
– число колебаний, - их время.
- их время.Повторить опыт 5 раз. Вычислить среднее значение квадрата периода
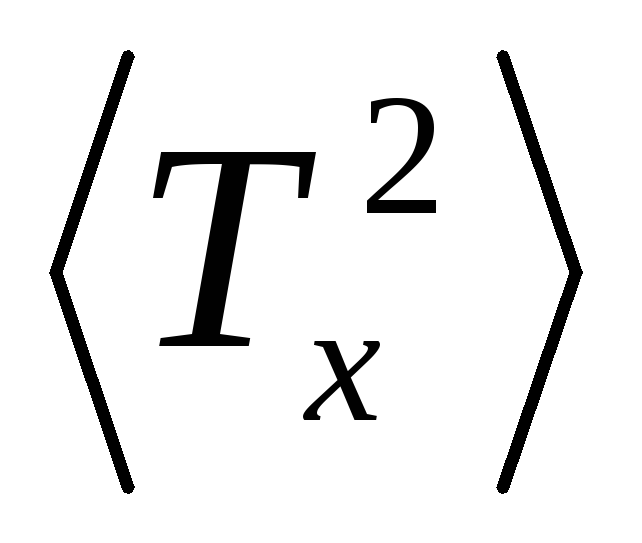 .
Вычислить среднее квадратичное
.
Вычислить среднее квадратичное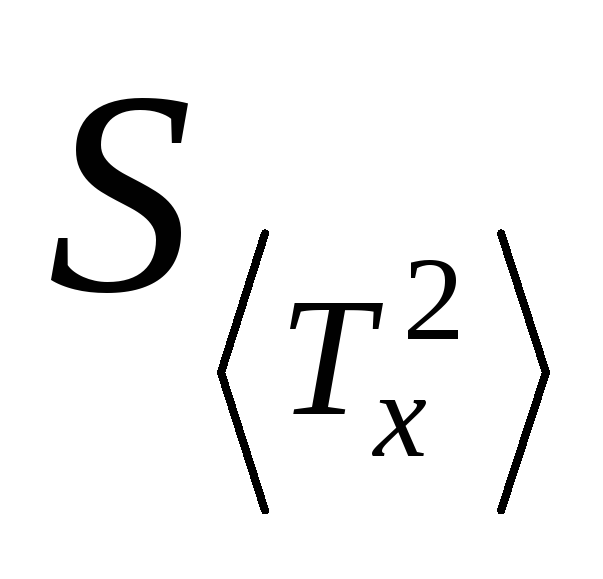 по формуле (19).
по формуле (19).Поочередно закрепляя образец относительно двух других главных осей, повторить эксперимент согласно пунктам 4 – 8, определив, таким образом, средние квадраты периодов
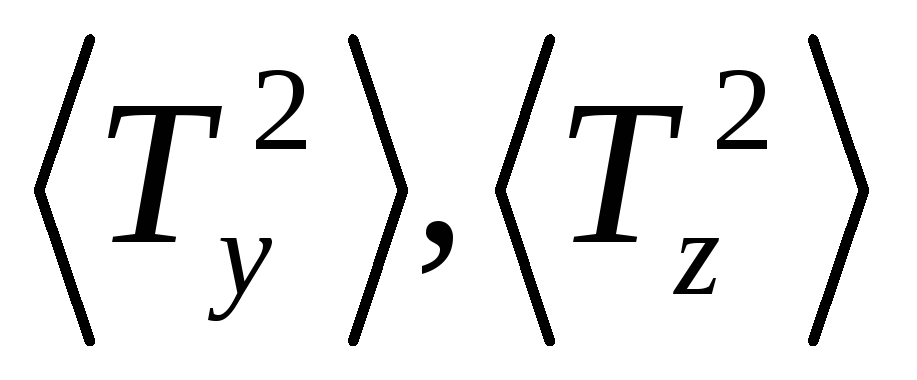 .
Заполнить таблицу 1.
.
Заполнить таблицу 1.Образец №
a, m
b, m
c, m
a2, m2
b2, m2
c2, m2
r2, m2
a4, m4
b4, m4
c4, m4
№
Tx, c
T2x
Tx - <T2x>
(Tx - <T2x>)2
Ty, c
T2y
Ty -<T2y>
(Ty - <T2y>)2
Tz, c
T2z
Tz - <T2z>
(Tz - <T2z>)2
Tэксп, c
1
…
5
Закрепить образец вдоль его пространственной диагонали. Повторить эксперимент, описанный в пунктах 4. – 8. Данные занести в таблицу.
Определить доверительный интервал, используя формулу (19). Записать ответ в виде:
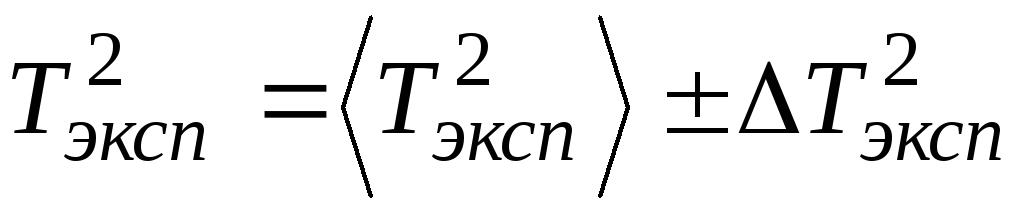 .
.Рассчитать среднее значение периода колебаний относительно оси, совпадающей с пространственной диагональю образца, определить доверительный интервал, используя формулы (20) и (21). Записать результат в виде:
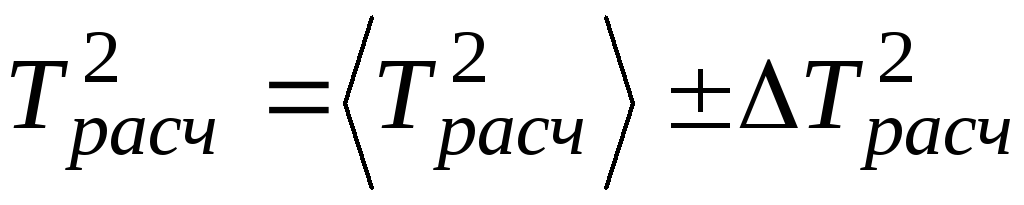 .
.Сравнить
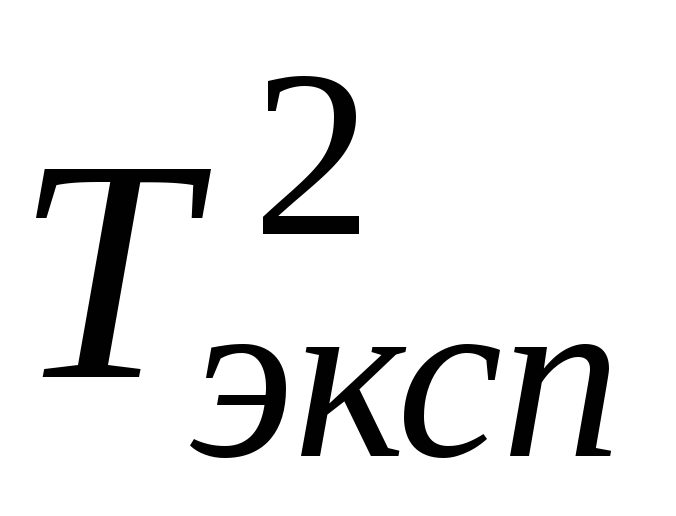 и
и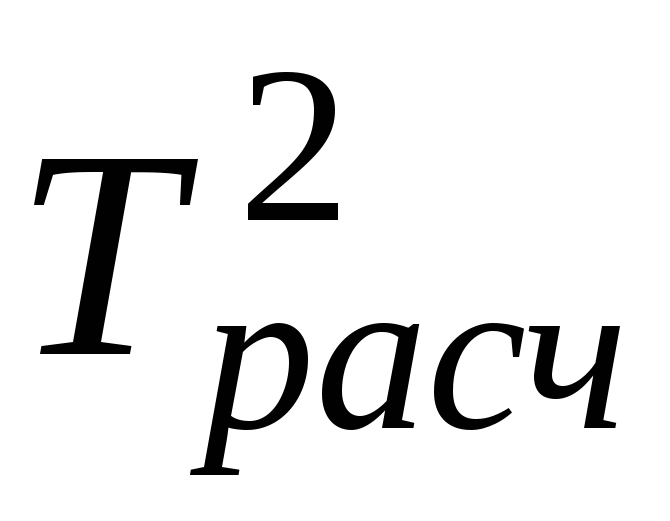 .
Сделать вывод.
.
Сделать вывод.Повторить весь эксперимент для другого образца.
