Инфлюентный анализ

Суть инфлюентного анализа состоит в оценке влияния A(x_t) параметров х_i на величину изменений показателя Y.

В этом случае Y представляется в виде алгебраической суммы

.

Составляющие разложения A(Dx_t) приращения Y называются инфлю-ентами, и задача инфлюентного анализа состоит в их нахождении, для того чтобы затем, по значениям инфлюент, определять направленность и степень влияния изменения параметров х_i = х_i⁽¹⁾ — х_i⁽⁰⁾ на изменение показателя Y = у⁽¹⁾ – у⁽⁰⁾. При этом значения (х_i⁽⁰⁾, у⁽⁰⁾, х_i⁽¹⁾, у⁽¹⁾ } называются терминальными, причем у⁽¹⁾ и х⁽¹⁾ рассматриваются как некоторые фактические (реальные, существующие), а у⁽⁰⁾ и х_i⁽⁰⁾ - как те, которых надо достичь (например, плановые, номинальные, желаемые).

При имеющейся математической модели Y = f(х₁, х₂, ..., х_n) наиболее простым методом является метод цепных подстановок, сущность которого заключается в подстановке в функцию Y в определенном порядке номинальных х_i⁽⁰⁾ и фактических х_i⁽¹⁾ параметров и вычислении инфлюент по cледующим простым формулам:

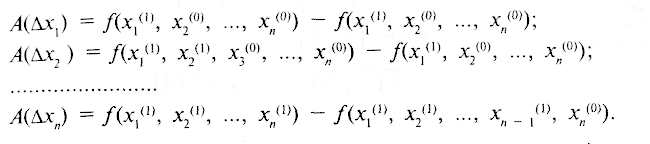
Недостатком метода является отсутствие правила перебора последовательностей индексов i для подстановки параметров (х_i⁽⁰⁾, х_i⁽¹⁾) и, как следствие, зависимость инфлюент от выбранной последовательности. Этого недостатка лишены более сложные процедуры расчета инфлюент, рассматриваемые в работах Р.И. Трухаева [6.59; 6.60].

По значениям инфлюент ранжируют влияние параметров системы на ее показатели, определяют направленность этого влияния, выделяют долю влияния каждого параметра относительно других.

Инфлюентный анализ ориентирован в основном на решение экономических задач, а также может быть использован и для исследования сложных технических систем управления (см. [6.44]).

6.6Cинтез систем управления методами оптимизации

¨ синтез систем управления методами безусловной оптимизации

¨ синтез систем управления с помощью многокритериальной оптимизации

Синтез систем управления методами безусловной оптимизации

Сущность и область применения

Сущность методов безусловной оптимизации состоит в поиске минимуму функции Y = Дх) путем многократных вычислений, при различных значениях параметров х = {x^k}, k = 0, 1, 2, ..., причем на каждом k-м шаге вычислений контролируют выполнение условий

,

которые должны привести к минимальному значению функции.

Основные трудности применения заключаются в определении шага изменения параметра x^(k), направления этого изменения и начального приближения x⁽⁰⁾.

Методы безусловной оптимизации используются для однокритериальной оптимизации детерминированных функций при отсутствии ограничений на саму функцию или ее параметры. Наиболее употребительны: методы первого порядка и методы второго порядка.

Эти методы и их модификации широко представлены в общем математическом обеспечении ПЭВМ (см. [6.12; 6.41]).

Методы нулевого порядка

Методы нулевого порядка используют, если производную исследуемой функции найти нельзя или существуют разрывы функций.

Метод покоординатного спуска. Сущность метода состоит в том, что производится раздельная оптимизация по параметрам функций: один из параметров считается изменяемым, а остальные фиксируются при некоторых значениях; затем изменяемым становится следующий параметр, а предыдущий принимает значение, полученное при предыдущей оптимизации (на предыдущем шаге). Процесс продолжается до окончания перебора всех параметров. Метод прост в реализации и эффективен для малого числа параметров.

Метод конфигураций. Сущность метода заключается в поиске направления изменения параметров относительно некоторой выбранной начальной точки (строится конфигурация направления поиска). Вначале обследуют ее окрестность (по параметрам) и выбирают направление изменения параметров, ориентируясь на уменьшение исследуемой функции. Выбрав направление, начинают движение большими шагами до тех пор, пока функция уменьшается. Если этот процесс прекратился (либо его совсем не произошло), то шаг уменьшают с целью определения точки, от которой прекратилось уменьшение функции. Затем процесс повторяют от новой базовой точки или изменяют направление от предыдущей. Метод используется для задач с большим числом параметров, когда покоординатный спуск становится неэффективным (см. [6.44]).

Метод случайного поиска. Метод имеет большое количество модификаций. Общее для них состоит в использовании элемента случайности (путем розыгрыша случайного события) при определении направления поиска и величины шага изменения параметров. Метод эффективен для сложных систем с большим числом параметров (см. [6.44]).

Методы первого порядка

Методы первого порядка используют, если возможно найти первую производную исследуемой функции. К данному классу относятся градиентные методы. Их суть заключается в определении лучшего направления и шага поиска минимума функции по значениям первых производных в некоторой точке х^(k). Наибольшее значение производной показывает направление наискорейшего уменьшения функции, и в этом направлении рассчитывается следующее приближение функции у = f(x^(k+1)), параметры которой отличаются на величину некоторого шага х. В зависимости от способа задания этого шага и производится классификация градиентных методов: градиентный спуск; наискорейший спуск; градиентный спуск с постоянным шагом; градиентный спуск с переменным шагом. Методы эффективны Для функций со слабовыраженной нелинейностью (см. [6.44]).

Методы второго порядка

Методы второго порядка используют, если возможно найти вторую производную исследуемой функции. Их основой является метод Ньютона, предполагающий аппроксимацию исследуемой функции Y = f(x) квадратичным полиномом в окрестностях некоторой точки x^(k) (точки начального приближения). Следующее приближение x^(k+1) определяется путем минимума квадратичной аппроксимации функции F(x), т.е. такой точки в окрестности x^(k) в которой вид функции в наибольшей степени "похож" на квадратичную. Различные модификации метода Ньютона в основном отличаются друг от друга способами расчета вторых производных. Методы второго порядка сходятся быстрее градиентных, однако требуют вычислений вторых производных (см. [6.44]).