Введение

В данном методическом пособии рассматриваются вопросы, входящие в университетский курс по дискретной математике. Большой раздел посвящён проблемам полноты булевых функций. В нём изложены основные определения и результаты по данной проблематике: теорема о представлении булевой функции в виде совершенной дизъюнктивной (конъюнктивной) нормальной формы, полинома Жегалкина, критерий Поста полноты, базисы в предполных классах. Следующий раздел посвящён проблемам минимизации представления булевых функций в виде ДНФ: геометрическая интерпретация, покрытия, интервалы, метод построения сокращённой и минимальных ДНФ. В заключение излагаются основы классического исчисления высказываний: основные определения, теорема дедукции, полнота исчисления высказываний.

Все разделы снабжены большим количеством учебных примеров и задач.

Пособие создано на основе программы первого семестра курса лекций по дискретной математике, читавшегося в Волгоградском государственном университете.

Дискретная математика

Булевой функцией f(x₁ … x_n) называют функцию, аргументы которой принимают значения из множества {0;1} и значение функции также из множества {0;1}.

1.Табличные способы задания булевых функций :

x1	…	xn	f(x1…xn)
0	…	0	*
0	…	1	*
…	…	…	…
1	…	1	*

В начале выписываются двоичные наборы из n нулей и единиц. Это удобно делать в двоичной системе счисления – то есть начиная с нуля прибавлять единицу в двоичной системе счисления. На каждом наборе надо задать значение функции.

Пример табличного задания функции:

x1	x2	x3	f(x1 x1 x3)
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	0

2.Основные булевые функции и их таблицы.

0 – константа ноль ;

1 – константа один ;

x - тождественная ;

- отрицание ;

- конъюнкция (логическое умножение) ;

- дизъюнкция (логическое сложение) ;

+ - модульная сумма ;

~ - эквиваленция (отрицание модульной суммы) ;

- следствие .

x1	x2	cnst 0	cnst 1	x1		x1x2	x1x2	x1+ x2	x1 ~ x2	x1x2
0	0	0	1	0	1	0	0	0	1	1
0	1	0	1	0	1	0	1	1	0	1
1	0	0	1	1	0	0	1	1	0	0
1	1	0	1	1	0	1	1	0	1	1

3.Свойства булевых функций :

Определения.

Бинарная операция ассоциативна, если тождественно выполняется: ;

бинарная операция коммутативна, если тождественно выполняется: ;

бинарная операция дистрибутивна по отношению к бинарной операции , если тождественно выполняется:

;

Утверждение 1. ,конъюнкция ассоциативна.

x1	x2	x3	x2 x3	x1(x2x3)	x1x2	(x1x2) x3
0	0	0	0	0	0	0
0	0	1	0	0	0	0
0	1	0	0	0	0	0
0	1	1	1	0	0	0
1	0	0	0	0	0	0
1	0	1	0	0	0	0
1	1	0	0	0	1	0
1	1	1	1	1	1	1

Утверждение 2. ,

дизъюнкция ассоциативна.

x1	x2	x3	x2 x3	x1(x2 x3)	x1x2	(x1x2 )x3
0	0	0	0	0	0	0
0	0	1	1	1	0	1
0	1	0	1	1	1	1
0	1	1	1	1	1	1
1	0	0	0	1	1	1
1	0	1	1	1	1	1
1	1	0	1	1	1	1
1	1	1	1	1	1	1

Утверждение 3. ,конъюнкция

коммутативна; , дизъюнкция также

коммутативна;

x1	x2	x1x2	x2x1
0	0	0	0
0	1	0	0
1	0	0	0
1	1	1	1

Предложение 1. Результат выполнения ассоциативной операции не зависит от расположения скобок в скобочном выражении.

Например: Если ассоциативная операция, тогда

.

Доказательство предлагается в качестве домашнего упражнения.

Примечание: использовать индукцию по числу скобок в выражении.

Из того, что конъюнкции и дизъюнкции ассоциативные операции, результат конъюнкции или дизъюнкции нескольких переменных не зависит от расположения скобок.

Например:

Тогда в силу независимости значения выражений конъюнкций от расположения скобок корректно определение как значение логического произведения при каком-либо порядке расположения скобок. Точно также для дизъюнкции.

Предложение 2. Конъюнкция равна 0, т. и т.т., когда хотя бы один из множителейравен 0.

Дизъюнкция равна 1, т. и т.т., когда хотя бы одно из слагаемыхравно 1.

Доказательство предлагается в качестве домашнего упражнения.

Утверждение 4.

, конъюнкция дистрибутивна по отношению к дизъюнкции.

x1	x2	x3	x2 x3	x1(x2x3)	x1x2	x1x3	(x1x2 )(x1x3 )
0	0	0	0	0	0	0	0
0	0	1	1	0	0	0	0
0	1	0	1	0	0	0	0
0	1	1	1	0	0	0	0
1	0	0	0	0	0	0	0
1	0	1	1	1	0	1	1
1	1	0	1	1	1	0	1
1	1	1	1	1	1	1	1

Утверждение 5.

, дизъюнкция дистрибутивна по отношению к конъюнкции.

x1	x2	x3	x2x3	x1(x2x3)	x1x2	x1x3	(x1x2)(x1x3)
0	0	0	0	0	0	0	0
0	0	1	0	0	0	1	0
0	1	0	0	0	1	0	0
0	1	1	1	1	1	1	1
1	0	0	0	1	1	1	1
1	0	1	0	1	1	1	1
1	1	0	0	1	1	1	1
1	1	1	1	1	1	1	1

Утверждение 6. , следствие не ассоциативная операция.

x1	x2	x3	x2x3	x1(x2x3)	x1x2	(x1x2)x3
0	0	0	1	1	1	0
0	0	1	1	1	1	1
0	1	0	0	0	1	1
0	1	1	1	1	1	1
1	0	0	1	1	0	1
1	0	1	1	1	0	0
1	1	0	0	0	1	1
1	1	1	1	1	1	1

Утверждение 7.

x1	x2	x3	x2x3	x1(x2x3)	x1+x2	x1+x3	(x1+x2)(x1+x3)
0	0	0	0	0	0	0	0
0	0	1	0	0	0	1	0
0	1	0	0	0	1	0	0
0	1	1	1	1	1	1	1
1	0	0	0	1	1	1	1
1	0	1	0	1	1	0	0
1	1	0	0	1	0	1	0
1	1	1	1	0	0	0	0

Утверждение 8.

,

конъюнкция дистрибутивна по отношению к сумме по модулю два.

x1	x2	x3	x2+x3	x1(x2+x3)	x1x2	x1x3	(x1x2)+(x1x3)
0	0	0	0	0	0	0	0
0	0	1	1	0	0	0	0
0	1	0	1	0	0	0	0
0	1	1	0	0	0	0	0
1	0	0	0	0	0	0	0
1	0	1	1	1	0	1	1
1	1	0	1	1	1	0	1
1	1	1	0	0	1	1	0

Определение. Две функции назовем одинаковыми, если они зависят от одного и того же набора переменных и их значения совпадают на каждом из наборов своих переменных.

Теорема: Число различных булевых функций от n переменных есть .

Теорема будет следовать из следующего утверждения:

число различных двоичных наборов длины n есть 2ⁿ (под длиной набора подразумевается число цифр в нем).

Докажем утверждение индукцией по длине n набора.

Для n=1 имеем 0;1 два различных набора длины 1;

2¹ =2. Для n=1 утверждение индукции справедливо.

Пусть утверждение индукции справедливо для n1, то есть число различных двоичных наборов длины n1 есть  2ⁿ.

Покажем справедливость утверждения для n=n+1. Разобьем все двоичные наборы длины n+1 на две группы. В первую группу отнесем двоичные наборы, которые начинаются на 0. Во вторую группу отнесем двоичные наборы, которые начинаются на 1, например, для n+1 = 3 будет такое разбиение:

0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

Двоичные наборы первой (второй) группы получаются из всевозможных двоичных наборов длины n добавлением слева нуля (единицы) к всевозможным наборам длины n.

Но по предположению индукции наборов длины n имеется 2ⁿ, поэтому число наборов как в первой, так и во второй группе будет 2ⁿ, поэтому общее число наборов длины (n+1) будет 2ⁿ+2ⁿ = 2ⁿ2 = 2ⁿ⁺¹

Утверждение доказано.

x1	…	xn	f(x1…xn)
0	…	0	*
2n …	…	…	…
1	…	1	*

Функций от n переменных будет ровно столько, сколько существует разных двоичных наборов длины 2ⁿ.

По предыдущему утверждению это число есть . Теорема доказана.

Определение :

Переменная x булевой функции f(x…) называется существенной, если существует набор значений остальных переменных функции, что изменение значения переменной при данном наборе остальных переменных изменяет значение функции.

Пример: x₁ и x₂  существенные переменные

x₃  не существенная переменная

x1	x2	x3	f
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	1

Определение :

Элементарной конъюнкцией на множестве переменных {x₁…x_n} называют функцию логического произведения множителей , где каждый множитель либо переменная, либо отрицание переменной.

В дальнейшем значение в элементарной конъюнкции будем опускать или заменять.

Например: { x₁ x₂ x₃ x₄ }

x₁ x₂ x₄ ; эта функция равна 1, только на одном наборе:

1 0 1 , тогда x₁ x₂ x₄=1

x₁ x₂ x₄

Рангом конъюнкции называют число переменных конъюнкции. Далее будем считать, что все переменные в множителях элементарных конъюнкций различны. В противном случае , используя правила :

, приведем конъюнкции к нужном виду;

Например:

полученная конъюнкция будет тождественно равна первоначальной.

В силу коммутативности бинарной конъюнкции, две элементарные конъюнкции одинаковы, т . и т. т., когда они состоят из одного набора множителей.

Определение :

Элементарной дизъюнкцией на множестве переменных {x₁…x_n} называют функцию логического сложения слагаемых , где каждое слагаемое либо переменная, либо отрицание переменной.

Например: { x₁ x₂ x₃ x₄

x₁ x₂ x₄ ; эта функция равна 0, т. и т.т., когда все слагаемые равны 0.

0 1 0

x₁ x₂ x₄

Рангом конъюнкции называют число переменных конъюнкции. Далее будем считать, что все переменные в множителях элементарных конъюнкций различны . В противном случае , используя правила :

приведем дизъюнкции к нужном виду; полученная дизъюнкция будет тождественно равна первоначальной.

В силу коммутативности дизъюнкции, две элементарные дизъюнкции одинаковы, т . и т. т., когда они состоят из одного и того же набора слагаемых.

Дизъюнктивной нормальной формой (ДНФ) на множестве переменных (x₁…x_n) называют функцию логического сложения некоторых слагаемых, где каждое слагаемое есть элементарная конъюнкция на (x₁…x_n) :

{ x₁ x₂ x₃ x₄ }

ДНФ называется совершенной (СДНФ), если каждая элементарная конъюнкция имеет ранг n :

Множество единиц ДНФ есть объединение множества единиц элементарных конъюнкций ДНФ. Для СДНФ каждая элементарная конъюнкция имеет единственную единицу.

Теорема о представлении любой булевой функции в виде СДНФ : для любой булевой функции справедлива следующая формула :

x1	x2	x3	f
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	0

Доказательство:

Свойства

1)

2)

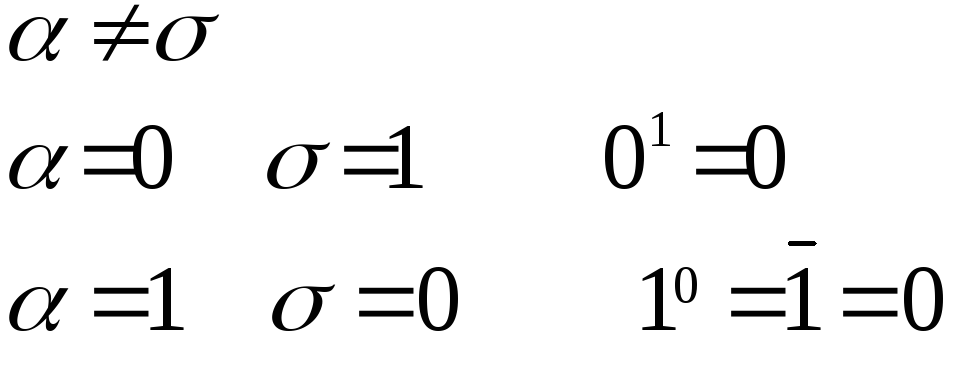
Чтобы доказать теорему покажем выполнение данного равенства на любом двоичном наборе ,то есть что левые и правые части совпадают для любого двоиного набора:

.

. То есть левая часть равенства равна 1. Покажем,что и правая часть равенства также равна 1 на данном наборе. Для этого достаточно показать,что хотя бы одно слагаемое правой части равно 1.

Таким слагаемым будет слагаемое, которое соответствует единичному набору , совпадающего с набором .

.

Значение этого слагаемого на наборе есть

в силу того ,что значение каждого множителя равно 1. Последнее справедливо в силу свойства символа .

. То есть левая часть равна 0. Покажем, что и правая часть также равна 0. Для этого нужно показать, что значение всех слагаемых равно 0. Рассмотрим произвольное слагаемое правой части, которое соответствует некоторому двоичному набору , тогдав силу, того, что наборы и  различны, т.к.  - набор, на котором значение функции равно 0, а  - набор, на котором значение функции равно 1. Так как наборы различны, то существует множитель i: , а поэтому и все произведение равно 0.Таким образом каждое слагаемое равно 0, следовательно и вся сумма равна 0, значит правая часть равна 0.

Теорема полностью доказана.

x1	x2	x3	f
0	0	0	0	0	0	0	0
0	0	1	0	0	0	0	0
0	1	0	1	1	0	0	1
0	1	1	0	0	0	0	0
1	0	0	1	0	1	0	1
1	0	1	1	0	0	1	1
1	1	0	0	0	0	0	0
1	1	1	0	0	0	0	0

Теорема о разложении булевой функции по первым k-переменным.

Доказательство:

Рассмотрим произвольный набор значений переменных , и покажем, что левая и правая часть равны. Левая часть -.

В правой части рассмотрим слагаемое, в котором значение набора  совпадает с первыми k-компонентами набора : .

Значение этого слагаемого на наборе равно.

В силу того, что набор  и первые k-компонент набора  совпадают, рассматриваемые множители равны 1, все слагаемое равно . Все остальные слагаемые равны 0 в силу того, что среди множителейобязательно найдется множитель, в котором и  различаются, а это нулевой множитель. Поэтому правая часть равна (все слагаемые, кроме быть может одного, равны 0).

Теорема доказана.

Нетрудно убедиться в справедливости следующих тождеств:

1. 6)

2. 7)

3. 8)

4. 9)

5. 10)

Доказательство предлагается в качестве домашних упражнений.

Последние два тождества называются правилами Де-Моргана.

Определение.

Двойственной к функции называют функцию .

Например, двойственной к конъюнкции является

дизъюнкция, и наоборот, двойственной к дизъюнкции является конъюнкция.

0 0 0 0

0 1 0 1

1 0 0 1

1 1 1 1

Утверждение. Двойственной к двойственной функции есть сама функция, т.е.

Теорема о представлении булевой функции в виде конъюнктивной нормальной формы .

КНФ называют логическое произведение некоторых сомножителей, где каждый сомножитель есть элементарная дизъюнкция. КНФ от переменных {x₁…x_n} называется СКНФ, если каждая дизъюнкция полного ранга, то есть в каждую дизъюнкцию входят все n переменных.

Пример: { x₁ x₂ x₃ }

КНФ :

СКНФ:

Теорема о представлении любой булевой функции в виде СКНФ.

Пример:

x1	x2	f
0	0	0
0	1	1
1	0	0
1	1	0

Доказательство : рассмотрим произвольный набор значений переменных . Либо, либо.

1. Левая часть равенства равна 1. Покажем, что и правая часть равна единице. Рассмотрим произвольный множитель правой части . Значение этого множителя на набореравнот.к. существует i такое, что, что верно в силу того, что - набор, на котором значение f () = 1, а  - набор, на котором значение f()= 0, то есть  и  - два различных набора, а поэтому есть компонента, в которой они отличаются.

Поэтому ; т.к.,.

2. Пусть . Покажем, что и правая часть равна 0. Для этого достаточно показать, что существует множитель, который равен 0 на наборе. Действительно, рассмотрим множитель соответствующий набору правой части , который совпадает с набором.

В силу того, что есть ноль функции, наборсуществует. Тогда значение рассматриваемого множителя на наборе равно

(т. к.для всех i :). А так как существует множитель, равный 0, то и значение всей СКНФ = 0.

Теорема о разложении булевой функции по первым k переменным .

Для любой булевой функции f(x₁…x_n) тождественно выполнено :

Доказательство. Рассмотрим произвольный набор . Значение левой части есть.

В правой части множитель, в котором будет равен 1 в силу того, что, тогдав силу того, что, а раз некоторое слагаемое равно 1 , вся элементарная дизъюнкция равна 1. Тогда остается один множитель, который равен

Тогда все произведение есть . Что и требовалось доказать.

Определение : Полиномом Жегалкина называется сумма по модулю 2 (+) некоторого количества слагаемых, где каждое слагаемое есть элементарная конъюнкция переменных без отрицания.

Пример:

1+x₁x₂+x₃+x₁x₄x₅

Полином Жегалкина, не содержащий ни одного слагаемого, равен 0.

Далее будем рассматривать так называемые приведенные полиномы Жегалкина, т.е. полиномы, в которых все слагаемые различные конъюнкции.

Например 1+x₁x₂+x₃+x₁x₄x₅ (нет двух одинаковых слагаемых).

Если некоторые слагаемые повторяются, то используя правило x+x=0, нетрудно привести любой полином к приведенному виду.

Например x₁x₂+x₃+x₁x₂+x₁x₄x₅+x₃=x₁x₄x₅

Если слагаемое повторяется нечетное количество раз, то оставляем его в единственном экземпляре.

Теорема о представлении булевой функции в виде полинома Жегалкина .

Для любой булевой функции существует представление в виде полинома Жегалкина и это представление единственно.

Доказательство:

Пример 1:

x1	x2	x3
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	0

Первая часть теоремы следует из теоремы о представлении булевой функции в виде СДНФ. А именно рассмотрим для булевой функции ее СДНФ. Далее операцию выразим через операциюпо правилу Де Моргана.

После чего операцию выразим через операциюи приведем полученную формулу к нормальному виду полинома Жегалкина раскрыв скобки в полученном выражении, используя дистрибутивность конъюнкции по отношению к сумме по модулю два. Для функции из примера1 СДНФ имеет вид :

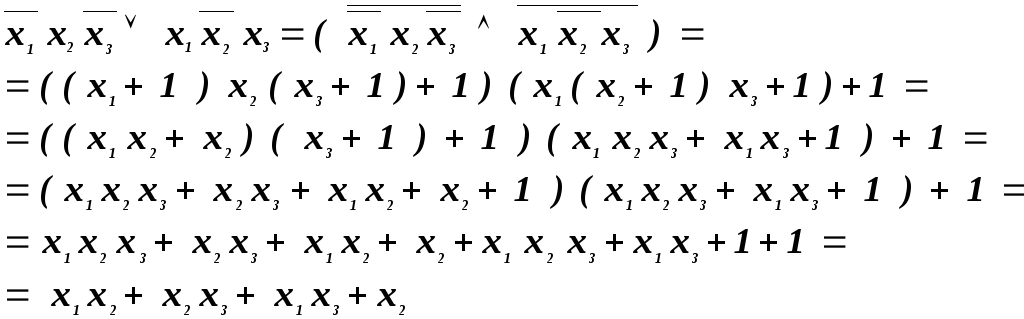
Покажем, что полученный полином единственен с точностью до перестановки слагаемых и множителей в слагаемых полинома.

Допустим противное : , которая имеет два различных полинома Жегалкина:

Из этих равенств следует,что

прибавим к обеим частям равенства :

В силу того, что иразличные полиномы Жегалкина, либо весть слагаемое, которого нет в, либо наоборот. Поэтому приведенный полиномотличен по форме от нуля, т.е. в этом полиноме присутствуют слагаемые, не тождественно равные нулю, и полином тождественно равен константе ноль :.

Далее рассмотрим слагаемое полинома , содержащее наименьшее число переменных. Теперь рассмотрим набор значений переменных, в котором переменные данного слагаемого равны 1, а все остальные слагаемые равны 0. Тогда, нетрудно видеть, что значениена таком наборе равно 1, в то время какна всех наборах. Противоречие.

Упражнение: найдите полином Жегалкина следующих функций :

1) 4)

2) 5)

3) 6)

Определение: суперпозицией булевых функции

называется функция

, полученная путем подстановки

функциив функциювместо некоторой переменной:.

Переименование переменных есть частный случай суперпозиций : , в которой вместоподставлена функция, то естьпереименованна в.

Определение: замыканием системы функцийназывается множество функций, полученных из функцийвсевозможными суперпозициями.

Пример 1:

(все функции рассматриваются с точностью до переименования переменных; например, исчитаются эквивалентными) :

Пример 2:

Определение : замкнутой системой функции называют систему, замыкание которой совпадает с самой системой .

Пример 3:

Определение: система функций называется полной, если ее замыкание совпадает с классом всех булевых функций.(По другому говоря, с помощью суперпозиций функций из системы можно получить любую булеву функцию.)