
8.4. Непрерывность функции нескольких переменных ìãòó ìã ó
Пусть задана функция нескольких переменных f : A ⊂ Rn → R. Каждая точка a ∈ A являет- ся либопредельной точкой множества A, либоего изолированной точкой. В первом случае функция f может иметь в этой точке предел по множеству A, что приводит к следующемуопределению.
Ò

Определение
8.11.
Функцию
нескольких
переменных f
:
A
⊂
Rn
→
R
называют
непре-
![]() рывной
в
точке
a
∈
A,
предельной
для множества
A,
если
существует
предел
функции f
рывной
в
точке
a
∈
A,
предельной
для множества
A,
если
существует
предел
функции f
ÔÍ-12
ÔÍ-12

при
x→A
a,
равный
значению
функции в
этой
точке,
т.е.
если
lim f (x) = f (a). (8.5)
xA→a
![]()
Как оговорено в определении, точка a не только принадлежит множеству A, но и являетсяего предельной точкой, поскольку рассматривается предел функции в точке a по множеству A.
Функцию f : A ⊂ Rn → Rm считают непрерывной в каждой точке a ∈ A, которая является
ÌÃÒÓ
ÌÃ Ó

изолированной точкой множества A.
Ò

Используя определение 8.9 предела функции, можно переформулировать определение непре- рывности функции в точке следующим образом. Функция f : A ⊂ Rn → R непрерывна в точкеa ∈ A, если для любойε-окрестности U(f (a), ε) точки f (a) ∈ R существует такая δ-окрест- ность U(a, δ) точки a, что при x ∈ A ∩ U(a, δ) верно соотношение f (x) ∈ U(f (a), ε). Наконец,
можно ввести понятие непрерывности, не используя ни понятие предела, ни понятие окрест- ности. Функция f : A ⊂ Rn → R непрерывна в точке a ∈ A, если для любого числа ε > 0 существует такое число δ > 0, что при всех x ∈ A, удовлетворяющих неравенству |x − a| < δ, верно неравенство |f (x) − f (a)| < ε. Другими словами, бесконечно малому приращению аргу-
ÔÍ-12
ÔÍ-12


мента в данной точке соответствуетбесконечно малое приращение функции. Отметим, что эти
формулировки включают в себя и случай изолированной точки множества A.
Функцию f
:
A
⊂
Rn
→
R,
непрерывную
во всех
точках
множества
A,
называют
непрерыв- ![]() ной на этом
множестве.
ной на этом
множестве.
Следующие так называемые локальные свойства непрерывных функций нескольких пере- менных вытекают из свойств 2–6 предела функции нескольких переменных (см. 8.3).
ÌÃÒÓ
ÌÃ Ó

1◦. Если функции fi: A ⊂ Rn → R, i = 1, k, непрерывны в некоторой точке a ∈ A, то любая
Ò

их линейная комбинация непрерывна в этой точке.
2◦.
Если функции
f,
g:
A
⊂
Rn
→
R
непрерывны
в некоторой
точке
a
∈
A,
то
их произведе-
ние fg,
а при
g(a)
/=
0
и частное
f/g
непрерывны
в этой
точке.
3◦. Если функция f : A ⊂ Rn → R непрерывна в точке a ∈ A, то она ограничена в пересече-
нии множества A с некоторой окрестностью точки a.
![]() 4◦.
Если
функция
f
:
A
⊂
Rn
→
R
непрерывна
в
точке
a
и
f
(a)
>
0
(f
(a)
<
0),
то
существует
окрестность
точки
a,
в
которой
функция
f
в
точках
множества
A
положительна
(отрицательна).
5◦.
Если
функции
f,
g:
A
⊂
Rn
→
R
непрерывны
в
точке
a
∈
A
и
f
(a)
<
g(a),
то
существует
4◦.
Если
функция
f
:
A
⊂
Rn
→
R
непрерывна
в
точке
a
и
f
(a)
>
0
(f
(a)
<
0),
то
существует
окрестность
точки
a,
в
которой
функция
f
в
точках
множества
A
положительна
(отрицательна).
5◦.
Если
функции
f,
g:
A
⊂
Rn
→
R
непрерывны
в
точке
a
∈
A
и
f
(a)
<
g(a),
то
существует
ÔÍ-12
ÔÍ-12


окрестность этой точки, в которой в точках множества A выполнено неравенство f (x) < g(x).
Отметим,
что в
сформулированных
свойствах
упоминание о
множестве
A
можно
опустить,
еслиточка a
являетсявнутренней
точкой множества
A.


![]()



![]()



![]() Для функций
нескольких
переменных,
как и
для функций
одного
переменного,
верна следу-
ющая теорема о непрерывностисложной
функции.
Для функций
нескольких
переменных,
как и
для функций
одного
переменного,
верна следу-
ющая теорема о непрерывностисложной
функции.
ÔÍ-12
ÔÍ-12


Теорема
8.6. Если
функции
gi:
A
⊂
Rm
→
R,
i
=
1,
n,
непрерывны
в
точке
a
∈
A,
(g1(x),
g2(x),
.
.
.
,
gn(x))
∈
B
⊂
Rn
при
x
∈
A
и
функция f
:
B
⊂
Rn
→
R
непрерывна в точке
b
=
(b1,
b2,
.
.
.
,
bn),
где
bi
=
gi(a),
i
=
1,
n,
то
сложная
функция
F
(x)
=
f
(g1(x),
g2(x),
.
.
.
,
gn(x)),
![]()
x ∈ A, непрерывна в точке a.
... Обозначим точку f (b) через c и фиксируем любую ε-окрестность U(c, ε) ⊂ R этой точки. Из непрерывности функции f в точке b следует, что существует такая δ-окрестность U(b, δ) ⊂ Rn точки b, что f (u) ∈ U(c, ε) при u ∈ B ∩ U(b, δ). Для каждого i = 1, n из непрерывности функции
Ò
δ
ÌÃÒÓ
ÌÃ Ó


gi в точке a следует, что для числа ε1 =
√n существует такая δi-окрестность U(a, δi) ⊂ R
m
точки
a,
что
gi(x)
∈
U(bi,
ε1)
при
x
∈
A
∩
U(a,
δi).
Положим
δ0
=
min
{δ1,
δ2,
.
.
.
,
δn}
и
выберем
произвольную точку x ∈ A ∩ U(a, δ0). Тогда gi(x) ∈ U(bi, ε1), что равносильно выполнению неравенства |gi(x) − bi| < ε1. Обозначив u = (g1(x), g2(x), . . . , gn(x)), заключаем, что
г 
ÔÍ-12
ÔÍ-12

I
n /
δ2
|u − b| = I' |gi(x) − bi| <
ε1n =
n = δ,
2 2
n
i=1
т.е.
u ∈
U(b,
δ). Включениеu ∈
B выполняется
в силуусловий
теоремы. Следовательно,
u ∈ B ∩ U(b, δ) и F (x) = f (g1(x), g2(x), . . . , gn(x)) = f (u) ∈ U(c, ε). Тем самым доказано, что
для произвольной окрестности U(c, ε) точки c существует такая окрестность U(a, δ0) точки a,
что F (x) ∈ U(c, ε) при x ∈ A∩ U(a, δ0). Согласно определению непрерывности функции в точке, это означает, что сложная функция F непрерывна в точке a. �
ÌÃÒÓ
ÌÃ Ó

Пример 8.15. Функция f (x, y) = e−y2/x2определена всюду в R2, кроме точек прямой x = 0.
Ò

В своей области определения эта функция непрерывна каккомпозиция непрерывных функций
e−t и t = y2/x2 (см. теорему 8.6). Функция t = y2/x2 является непрерывной в области x /= 0 как частное двух непрерывных функций (см. свойство 2 непрерывных функций).
В точках прямой x = 0 функция f (x, y) не определена, но, может быть, ее можно доопреде- лить в этих точках так, что она будет непрерывной в R2? Чтобы ответить на вопрос, возможноли такое доопределение, надо рассмотреть предел функции в точках прямой x = 0 по множеству
ÔÍ-12
ÔÍ-12

A
=
{(x,
y)
∈
R2:
x
/=
0}.
Существование
предела
функции
в
некоторой
точке
(x0,
y0)
необходи-
мо, чтобы вэтой точке было возможно доопределение функции по непрерывности, т.е.
такое доопределение, при котором функция будет непрерывной в точке (x0, y0).
Если y0
/=
0, то функцияy2/x2
являетсябесконечно
большой вточке
(0,
y0),
а функция![]() e−y2/x2
имеет предел
в этой
точке
по множеству
A,
равный нулю.
Но в
точке
(0,
0)
пределэтой функции
помножеству A
не существует.
Действительно,
рассмотриммножества
Ak
=
e−y2/x2
имеет предел
в этой
точке
по множеству
A,
равный нулю.
Но в
точке
(0,
0)
пределэтой функции
помножеству A
не существует.
Действительно,
рассмотриммножества
Ak
=
= {(x, y): y = kx, x /= 0}. Нетрудно увидеть, что y2/x2 = k2 при (x, y) ∈ Ak . Следовательно,
ÌÃÒÓ
ÌÃ Ó



lim
Ò
(x, y)A→k (0, 0)
f (x, y) = e−k2.
Предел
функции f
(x,
y)
в точке
(0,
0)
по множеству
Ak
зависит
от выбора
множества
Ak
.
Значит, в силуследствия 8.1
функцияf (x,
y)
не имеетпредела вточке
(0,
0) (см.
также при-
мер 8.12).
Итак, функцию f (x, y) нельзя доопределить так, чтобы она было непрерывной в точке (0, 0). Но подобное доопределение возможно в отношении других точек прямой x = 0, поскольку функ- ция
/
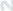
ÔÍ-12
ÔÍ-12


f-(x, y) =
(e−y2/x2, x = 0;
0, x = 0,
определена
в R2
и
непрерывна
всюду в
R2,
кроме
точки
(0,
0).



![]()



![]()



![]() Точки,
в которых
функция
нескольких
переменных
f
:
A
⊂
Rn
→
R
определена,
но
не явля-
етсянепрерывной,
называютточками
разрыва этой
функции.
Напомним, чтоточки,
в
Точки,
в которых
функция
нескольких
переменных
f
:
A
⊂
Rn
→
R
определена,
но
не явля-
етсянепрерывной,
называютточками
разрыва этой
функции.
Напомним, чтоточки,
в
ÔÍ-12
ÔÍ-12


которых функция исследуется на непрерывность, относятся кобласти определения этой функ- ции. Точка разрыва функции f : A ⊂ Rn → R должна быть точкой множества A, являющейся
для
A
предельной,
так как
в изолированных
точках
множества
A
функция
f
непрерывна
всегда
(см. 8.4). К точкам разрыва функции f часто относят и точки, которые являются предельнымиточками A, но самому множеству не принадлежат.
Точки разрыва могут образовывать подмножества в Rn, которые в зависимости от их вида называютлиниями илиповерхностями разрыва функции.
ÌÃÒÓ
ÌÃ Ó


Мы не будем определять различные типы точек разрыва, как это делают в случае действи- тельных функций действительного переменного, а ограничимся разбором типичных ситуаций на примерах.
Ò

Пример 8.16. а. Исследуем на непрерывность функцию двух переменных f (x, y) =
= 1/(1 − xy). Эта функция представляет собой частное двух непрерывных в R2 функций двух переменных (числитель — постоянная функция, а знаменатель — функция z(x, y) = 1 − xy).
ÔÍ-12
ÔÍ-12

Поэтому,
согласно
свойству 2
непрерывных
функций (см.
8.4),
она
непрерывна во
всех
точках,
вкоторых
знаменатель отличен от нуля,
т.е.
при1 −
xy /=
0. Множествоточек
в R2,
которое
описывается уравнением1
− xy
= 0,
является линией разрываэтой
функции.
В точках
этой
линии, являющейся равнобочной гиперболой, функция не определена.
б.
Функцияf (x,
y)
= sgn(xy)
определена
всюду вR2,
причем принимает всего лишь
три![]() значения:
значение 1
в точках
первого и
третьего
квадрантов
плоскости,
значение 0
на осях
значения:
значение 1
в точках
первого и
третьего
квадрантов
плоскости,
значение 0
на осях
координат и значение −1 вточках второго и четвертого квадрантов. Точками разрыва этой
функции являются точки на осях координат, а оси координат в данном случае являются лини-
ÌÃÒÓ
ÌÃ Ó

ями разрыва функции.
Ò

в. Функциятрех переменных
1
u =
1
−
x2
−
y2
−
z2
определена вне единичной сферы x2 + y2 + z2 = 1 и в точках области определения эта функция непрерывна как частное двух непрерывных функций. Оединичной сфере вэтом случае говорят
ÔÍ-12
![]() как о
поверхности
разрыва функции
u.
как о
поверхности
разрыва функции
u.
ÔÍ-12

г.
У функции трех
переменных
v = .j
−
1
1
x2
−
y2
−
z
2

область определения описывается неравенствомx2 + y2 + z2 < 1. Вэтой области функция непрерывна как частное двух непрерывных функций. Вточках единичной сферы и вне ее функция v не определена. Точек разрыва нет.
ÌÃÒÓ
ÌÃ Ó


д. Функция двух переменных
Ò

u = ln xy
определена
в области
xy
>
0,
т.е.
в первой
и третьей
четвертях без
осей координат.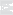
Пример 8.17. Исследуем на непрерывность функцию
(
xy
, x2
+
y2
/=
0;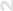
ÔÍ-12
ÔÍ-12

f
(x,
y)
=
x2 + y2
0, x = y = 0.

При x2
+ y2
/=
0 функцияf (x,
y)
является непрерывной как частное двух
непрерывных
функций.
В точке
(0,
0)
и ее
окрестности
функция
определена,
но
не
является
непрерывной вэтой
точке,
так какона
в нейне имеетпредела (см.
пример8.11). #


![]()



![]()



ЛЕКЦИЯ
8.
ФУНКЦИИ
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ КАК
ОТОБРАЖЕНИЯ 19

![]() Предположим,
чтофункция
нескольких переменных f
: Rn
→ R
определена в
некоторой
Предположим,
чтофункция
нескольких переменных f
: Rn
→ R
определена в
некоторой
ÔÍ-12
ÔÍ-12

окрестности
точки
a
=
(a1,
.
.
.
,
an).
Если
функция
g(x1) = f (x1, a2, a3, . . . , an),
которая
представляет
собой функцию
одного
действительного
переменного x1,
непрерывна
вточке x1
= a1,
то функциюf
называютнепрерывной
по переменному x1
в точке
a.
Непрерывность функции f = f (x1, x2, . . . , xn) по переменному x1 в точке a по определению означает, что существует предел
ÌÃÒÓ
ÌÃ Ó


lim
Ò
x1→a1
f (x1, a2, . . . , an) = f (a1, a2, . . . , an),
который
можно
рассматривать
как предел
в точке
a
по
множеству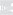
A1 = {(x1, . . . , xn) ∈ Rn: x2 = a2, . . . , xn = an} .
Аналогично вводят
понятие
непрерывности
функции f
(x)
в точке
a
по
остальным
перемен-
![]() ным: поx2,
поx3
и т.д.,
а также по произвольному набору ее
аргументов. Например,
если
ным: поx2,
поx3
и т.д.,
а также по произвольному набору ее
аргументов. Например,
если
ÔÍ-12
ÔÍ-12

функция двух
переменных
g(x1, x2) = f (x1, x2, a3, . . . , an)
непрерывна
в точке
x1
=
a1,
x2
=
a2,
то
функцию f
(x)
n
переменных
называют
непрерывной в
точке
a
по
части
переменных
(по
совокупности
переменных
)
x1,
x2.
Непре- рывность
по
части переменных
можно
рассматривать
как существование
предела
функции вточке
a
по
соответствующему
множеству.
Например,
непрерывность
функции f
(x1,
x2,
.
.
.
,
xn)
по
совокупности
переменных
x1,
x2
означает
существование
предела
ÌÃÒÓ
ÌÃ Ó


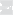
где
Ò
lim
x−→a
A
12
f (x) = f (a1, a2, . . . , an),
A12 = {(x1, . . . , xn) ∈ Rn: x3 = a3, . . . , xn = an} .
Отметим,
что из
непрерывности
функции
нескольких
переменных в
точке
a
следует
ее не-
прерывность вэтой
точке по
любому набору переменных,
поскольку если выполнено равенство
![]() lim
f
(x)
=
f
(a),
то,
согласно
следствию
8.1,
для любого
множества
A Rn,
длякоторого
точка
lim
f
(x)
=
f
(a),
то,
согласно
следствию
8.1,
для любого
множества
A Rn,
длякоторого
точка
⊂
ÔÍ-12
ÔÍ-12

x→a
a
предельная,
lim f (x) = f (a).
xA→a
В то же время,
даже если функция непрерывна вточке a
по любомунеполному
набору переменных,
это вовсе
не
значит,
что функция
непрерывна в
этой
точке.
Так,
функция f
(x,
y)
из примера 8.11 не является непрерывной в начале координат, но она непрерывна в этой точкепо каждому из переменных, т.е. по x и по y, поскольку f (0, y) ≡ f (x, 0) ≡ 0.
ÌÃÒÓ
ÌÃ Ó

Если функция нескольких переменных непрерывна по части своих переменных во всех точкахнекоторой области, то ее называют непрерывной в области по (этой) части переменных (совокупности переменных ).
Ò

Приведем без
доказательства свойствафункций
нескольких переменных,
непрерывных
на
компактах.
Теорема 8.7.
Пустьфункция
нескольких переменных f
: K
⊂ Rn
→ R
непрерывна накомпакте K.
Тогда:
ÔÍ-12
ÔÍ-12

функция f ограничена на K, т.е. существует такое число M > 0, что |f (x)| < M , x ∈ K;

функция f достигает на компакте K своих наибольшего и наименьшего значений, т.е. существуют такие точки x∗, x∗ ∈ K, что f (x∗) � f (x) � f (x∗), x ∈ K;
если компакт K — линейно связное множество, то для любого числа µ из отрезка
[f
(x∗),
f
(x∗)]
существует
точка
xµ
∈
K,
для
которой
f
(xµ)
=
µ. #


![]()



![]()





Ò
Ò
ÌÃÒÓ
ÌÃ Ó
ÌÃ Ó



ÌÃÒÓ
ÔÍ-12
ÔÍ-12
ÔÍ-12
ÔÍ-12








![]()
