Лабораторная работа № 1 первичная обработка результатов прямых многократных измерений /вычисление основных статистических параметров/

1. Цель работы

Освоить основные приемы статистической обработки данных многократных измерений на примере результатов математического эксперимента.

2. Задание

Используя возможности электронных таблиц Excel, получить выборку из нормального распределения. Оценить по выборке значения математического ожидания и среднеквадратического отклонения (СКО) генеральной совокупности, из которой извлечена выборка.

3. Краткая теория

Прямыми называются измерения, при которых искомое значение физической величины получают непосредственно с отчетного устройства средства измерения [2, 3]. Многократными называют измерения физической величины постоянного размера, повторенные несколько раз (не менее 4) при неизменных условиях. Задача состоит в том, чтобы найти оценку неизвестного истинного значения измеряемой физической величины. Обработка результатов многократных измерений производится методами математической статистики, где нет понятия «истинное значение», а используется понятие «математическое ожидание» как среднее значение по всей генеральной совокупности случайной величины. Однако для прямых измерений эти понятия оказываются адекватными, если ошибки измерений случайны и центрированы (имеют нулевое математическое ожидание).

Результаты измерений являются случайными величинами, то есть принимающими в зависимости от случая те или иные значения, заранее неизвестные и непредсказуемые. Каждое отдельное значение непрерывной случайной величины обладает нулевой вероятностью. Однако, нахождение возможных значений случайной величины в различных интервалах обладает различными и отличными от нуля вероятностями. Таким образом, для случайной величины можно определить закон распределения как функцию распределения случайной величины.

Функцией распределения случайной величины (интегральной функцией распределения) называется функция , задающая вероятность того, что случайная величинапринимает значение, меньшее, т.е.

. (1.1)

Кроме того, непрерывную случайную величину можно задать дифференциальной функцией распределенияилиплотностью распределения, которая позволяет дать представление о характере распределения случайной величины в небольшой окрестности некоторой точки числовой оси.

. (1.2)

График дифференциальной функции распределения называется кривой распределения. Кривая распределения, выражающая общую закономерность данного типа распределения, называетсятеоретической кривой распределения.

В статистике широко используются различные виды теоретических распределений, каждое из которых имеет специфику и свою область применения. Чаще всего в качестве теоретического распределения используется нормальное распределение¹, имеющее уравнение для плотности распределения

, (1.3)

а уравнение интегральной функции распределения –

, (1.4)

где – математическое ожидание случайной величины,– ее дисперсия, а– среднеквадратическое отклонение.

Параметры (числовые характеристики) закона распределения обычно остаются неизвестными. По выборке могут быть найдены лишь их оценки.

При многократных измерениях за результат измерений обычно принимается среднее арифметическое (СА):

. (1.5)

Иногда вместо СА используют выборочную медиану, которую при нечетном числе измерений находят по формуле:

, (1.6)

а при четном – по формуле:

, (1.7)

причем предварительно результаты измерений располагают в неубывающем порядке:. Такой порядок значений составляетвариационный ряд.

Реже используется выборочная мода как значение, соответствующее максимуму гистограммы (см. лаб. работу «Построение гистограммы…»).

Все эти оценки определяются по выборке и выражаются одним числом, то есть точкой на числовой оси, и называются точечными выборочными оценками математического ожидания (истинного значения физической величины).

Важными характеристиками точечных оценок являются следующие:

• несмещенность. Оценка (например,) параметра (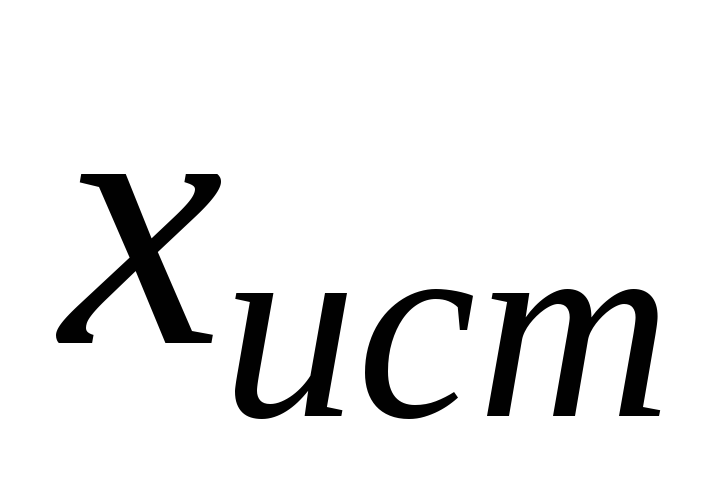) называется несмещенной, если ее математическое ожидание совпадает с оцениваемым параметром;

• состоятельность. Оценка называется состоятельной, если с увеличением объема выборки(число измерений) вероятность того, что оценка сходится к истинному значению, стремится к 1.

• эффективность. Оценка называется эффективной, если она обладает минимальной дисперсией по сравнению с другими оценками¹.

Чаще всего используется среднее арифметическое. Оно обладает следующими преимуществами перед другими оценками:

1. при любом законе распределения ошибок (с конечными математическим ожиданием и дисперсией) СА является несмещенной и состоятельной оценкой математического ожидания;

2. дисперсия СА в раз меньше дисперсии отдельных результатов измерений, то есть дисперсии ошибок;

3. в случае нормального распределения ошибок измерений СА является эффективной оценкой математического ожидания;

4. в случае нормального распределения ошибок измерений СА распределено нормально, а при других распределениях ошибок – асимптотически нормально. Причем с увеличением объема выборки распределение СА быстро сходится к нормальному.

Недостатком СА является то, что оно весьма чувствительно к промахам (грубым ошибкам).

Найденное по выборке случайных величин СА , является случайной величиной. Разность между ним и неизвестным истинным значениемназывается в статистике ошибкой, а в метрологии погрешностью. Она остается неизвестной и также является случайной величиной.

При неизвестной дисперсии (и неизвестном математическом ожиданииили истинном значении, если ошибки центрированы) ее точечной несмещенной и состоятельной, а при нормальном распределении ошибок и эффективной оценкой, является выборочная оценка дисперсии:

. (1.8)

Для вычисления оценки среднеквадратического отклонения по выборке обычно пользуются формулой:

. (1.9)

Для оценки среднеквадратического отклонения среднего арифметического пользуемся формулой, полученной из выражения (1.9) и свойства 2 среднего арифметического:

. (1.10)

Более подробные теоретические сведения см. в [4,5].

В работе предлагается выполнить расчеты двумя способами: с помощью аппарата статистических функций, а также используя надстройку ExcelПакет анализа. Последовательность установки и основы работы с Пакетом анализа смотри в прил. 1.