Подход к интегрированию рациональных дробей

Рациональная дробь(или рациональная функция) - это отношение двух многочленов.Многочлен n-той степенипредставляет собой выражение видаa_nxⁿ+a_n-1x^n-1+ …+ a₂x² + + a₁x + a₀, где a₀, a₁,…, a_n – действительные числа, a_n  0, n ≥ 0.

Будем рассматривать дроби, в которых степень знаменателя больше нуля (т.к. в противном случае в знаменателе стоит константа, и дробь представляет собой многочлен, интеграл от которого легко найти методом разложения).

Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя.

Например, (2x+ 7) – многочлен первой степени, (6x⁵+ 3x³+x) – многочлен пятой степени, - рациональная дробь, которая является правильной (в числителе вторая степень, а в знаменателе – пятая).

Отметим, что если дробь не является правильной, то ее можно представить в виде суммы многочлена и правильной дроби, используя алгоритм деления многочленов "углом". Например, , так как

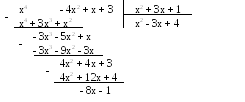
Тогда интеграл от исходной дроби сведется с помощью метода разложения к сумме интегралов от многочлена и правильной дроби. Поэтому имеет смысл рассмотреть только подход к интегрированию правильных дробей.

Если степень знаменателя равна единице, то искомый интеграл можно найти на основании теоремы о линейной подстановке и табличного интеграла, так как он имеет вид:

.

Пусть степень знаменателя равна двум, т.е. искомым является интеграл вида, гдеh,p,a0,bиc– вещественные числа.

Рассмотрим вначале случай, когда b= 0, т.е..

Тогда, если и с = 0, то , т.е. искомый интерграл можно найти методом разложения. Если

Если с 0, то. Первое слагаемое находят путем замены переменнойt=ax²+c. Тогдаdt= 2axdxиxdx=dt/2a:. Чтобы найти второе слагаемое, т.е., рассмотрим два варианта:

1) ас > 0, тогда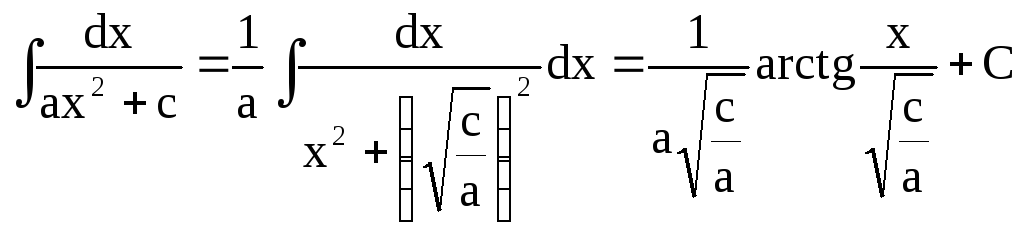

2) ас < 0, тогда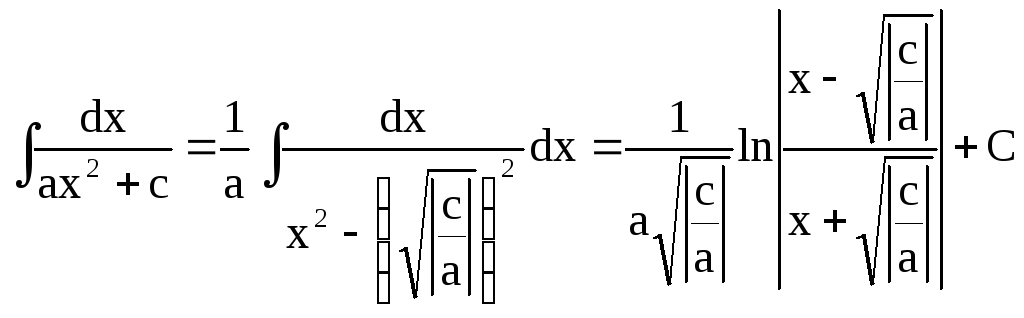

Каким образом свести общий случай к случаю? Для этого достаточно выделить в знаменателе подынтегральной функции полный квадрат, а затем использовать линейную замену переменной.

Рассмотренный прием интегрирования правильных дробей, знаменатель которых имеет вторую степень, основан на использовании методов разложения и подстановки. К сожалению, его недостаток заключается в том, что он не обобщается на случаи, когда степень знаменателя больше двух. В случаях, когда знаменатель правильной дроби – многочлен n–той степени, имеющийnдействительных корней, для нахождения интеграла используютметод неопределенных коэффициентов, который здесь подробно не рассматривается. Его можно найти в учебнике Кремера, стр. 272-273. Кроме того, в практикуме Кремера рассмотрен подход к интегрированию в случае, если таких корней может быть менееn(стр. 275).

Рационализация интегралов

Если подынтегральная функция не представляет собой рациональную дробь, то во многих случаях можно рационализировать интеграл(свести искомый интеграл к интегралам от рациональных функций) с помощью замены переменной.

Обозначим через R(u, v) некоторую рациональную функцию от переменных uи v

Рассмотрим интегралы вида . Их можно рационализировать заменой переменной. Частными случаями данного случая являются интегралы вида. Их также можно рационализировать такой же заменой переменной, гдеn– наименьшее общее кратное чиселn₁,n₂, …n_k.

Для рационализации интегралов вида используют подстановку.

Если под знаком радикала стоит многочлен второй степени, т.е. интеграл имеет вид , то иногда интеграл можно свести к табличному, выделив в подкоренном выражении полный квадрат, не рационализируя интеграл. В более сложных случаях ипользуютсяподстановки Эйлера, которые здесь не рассматриваются. Иногда такие интегралы удается рационализировать, используя для замены переменной тригонометрические функции, как это рассмотрено в практикуме Кремера на стр. 278.

Интегралы вида рационализируются с помощью тригономерических формул, выражающих синус и косинус через тангенс половинного аргумента и последующей замены переменнойt=tg(x/2). Подробно этот метод рассмотрен в учебнике Кремера на стр.276.

Пример 1.Найдем. В знаменателе подынтегральной функции стоят радикалы второй и третьей степеней. Наименьшим общим кратным для чисел 2 и 3 является число 6, поэтому осуществим замену переменной. Тогдаt⁶ = x, dx = 6t⁵dt, .

.

Еще раз осуществим замену переменной z=t+ 1.

Пример 2.Найдем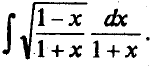Тогда

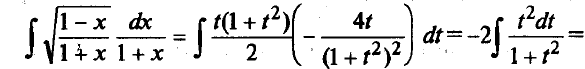
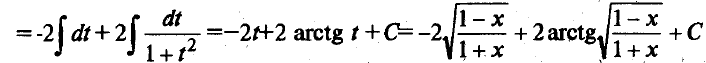
Из основных правил дифференцирования следует, что производная произвольной элементарной функции тоже является элементарной функцией. Операция нахождения неопределенного интеграла таким свойством не обладает, т.е. существуют элементарные функции, первообразные которых элементарными функциями уже не являются. Соответствующие неопределенные интегралы называются "неберущимися" в элементарных функциях, а сами функции - неинтегрируемымив конечном виде. Например, функцияявляется неинтегрируемой в конечном виде, так как не существует такой элементарной функции, чтобы ее производная равнялась этой функции.