
- •1.Числовая последовательность. Предел числовой последовательности. Сходящаяся последовательность. Теорема о единственности предела числовой последовательности.
- •2.Монотонные последовательности. Ограниченные последовательности. Теорема о сходимости монотонной ограниченной последовательности. Число е.
- •3.Функции: определение, способы задания. Основные элементарные функции, их графики. Свойство функций – монотонность, ограниченность. Обратная функция, сложная функция.
- •19.Классификация бесконечно малых функций.
- •20.Дифференциал функции, его геометрический смысл. Использование дифференциала при приближенных вычислениях.
- •21.Дифференцируемость функции в точке. Необходимое и достаточное условия дифференцируемости функции в точке.
- •28.Определение выпуклости функции. Признак выпуклости функции (без док). Точки перегиба.
- •29.Асимптоты графика функции.
- •35.Дифференцируемость функции двух переменных. Необходимое условие дифференцируемости. Полный дифференциал.
- •40.Условный экстремум функции двух переменных. Необходимое условие условного экстремума. Наибольшее и наименьшее значение непрерывной функции на замкнутом ограниченном множестве.
- •41.Первообразная функции. Теорема о множестве первообразных функций. Неопределенный интеграл.
19.Классификация бесконечно малых функций.
Предположим, что в каком-либо исследовании одновременно рассматривается ряд бесконечно малых величин a, b, g…, которые, вообще говоря, могут быть функциями от одной и той же переменной, стремящейся к конечному или бесконечному пределу.
Во многих случаях представляет интерес сравнение бесконечно малых между собой по характеру их приближения к нулю. В основу этого сравнения кладется поведение их отношения.
Определение 1. Если отношение b /a (a /b ) имеет конечный и отличный от нуля предел, то бесконечно малые a и b считаются (называются) величинами одного порядка малости.
Определение 2. Если отношение b /a само оказывается бесконечно малым (а обратное a /b - бесконечно большим), то бесконечно малая b считается величиной высшего порядка малости, чем бесконечно малая a , и одновременно бесконечно малая a будет величиной низшего порядка, чем бесконечно малая b .
20.Дифференциал функции, его геометрический смысл. Использование дифференциала при приближенных вычислениях.
Дифференциал независимого аргумента функции равен приращению этого аргумента.
Справедливо равенство ![]() .
Поэтому определение дифференциала моно
записать так –
.
Поэтому определение дифференциала моно
записать так –![]() ,
отсюда
,
отсюда ![]() .
.
Кроме производной в матане важное значение играет понятие дифференциала функции.
![]()
![]()
По основному свойству предела если функция имеет предел, то отличие функции от предела бесконечно мало.
![]()
![]()
э то
основное; главная линейная часть
приращения функции.
то
основное; главная линейная часть
приращения функции.
Определение 1. Главная линейная
часть приращения функции равная
произведению ![]() называется дифференциалом функции и
обозначается через dy.
По определению – dy=
называется дифференциалом функции и
обозначается через dy.
По определению – dy=![]()
Отметим, что дифференциал функции
отличается от её приращения на слагаемое
![]() .
.
Геометрический смысл дифференциала функции.
Придадим ![]() приращение
приращение
![]() ,
тогда при таком приращение аргумента
функция получит приращение f(
,
тогда при таком приращение аргумента
функция получит приращение f(![]() ).
Дифференциал – приращение, которая
получает касательная при приращении
аргумента.
).
Дифференциал – приращение, которая
получает касательная при приращении
аргумента.
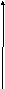



dy – приращение касательной.
![]()
Дифференциал – KM. (KM=dy)
![]()
![]()
![]()
Это приращение не самой функции, а
приращение касательной к графику этой
функции, проведенной в точке, в которой
вычисляется этот дифференциал (при
![]() ).
).
Так как приращение отличается от
дифференциала на (![]() ),
то на практике используется такое
),
то на практике используется такое ![]()
21.Дифференцируемость функции в точке. Необходимое и достаточное условия дифференцируемости функции в точке.
Функция y=f(x) называется дифференцируемой в точке x0, если ее приращение Δy в точке x0 может быть представлено в виде: Δy=A·Δx+α(Δx)·Δx, где A -- некоторое число, независящее от Δx, а α(Δx)-- бесконечно малая функция от переменной Δx, т.е.
![]()
Теорема Для того, чтобы функция y=f(x) была дифференцируема в точке x0, необходимо и достаточно, чтобы она в этой точке имела конечную производную. Доказательство Необходимость. Предположим: функция дифференцируема в точке x0, т.е. Δy=A·Δx+α(Δx)·Δx. Разделив обе части данного равенства на Δx, получим: ΔxΔy=A+α(Δx). Из определения производной функции в точке:
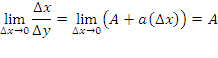
Т.е. получили, что существует конечная производная функции в точке x0 и y`(x0)=A. Достаточность. Пусть существует конечная производная y`(x0)∈R . Покажем дифференцируемость функции.
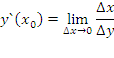
Если
функция f(x) имеет конечный предел b при
Δx→0 , то ее можно представить:
f(x)=b+α(x) (α(x)→0) . Исходя из этого:
![]() =y`(x0)+α(Δx),
где
=y`(x0)+α(Δx),
где
![]()
, Δy=y`(x0)·Δx+α(Δx)·Δx→ A=y`(x0) . Теорема доказана. Определение. Дифференциалом функции y=f(x) в точке x0 называется главная линейная относительно Δx часть приращения функции Δy в данной точке.
22.Теорема Ферма.
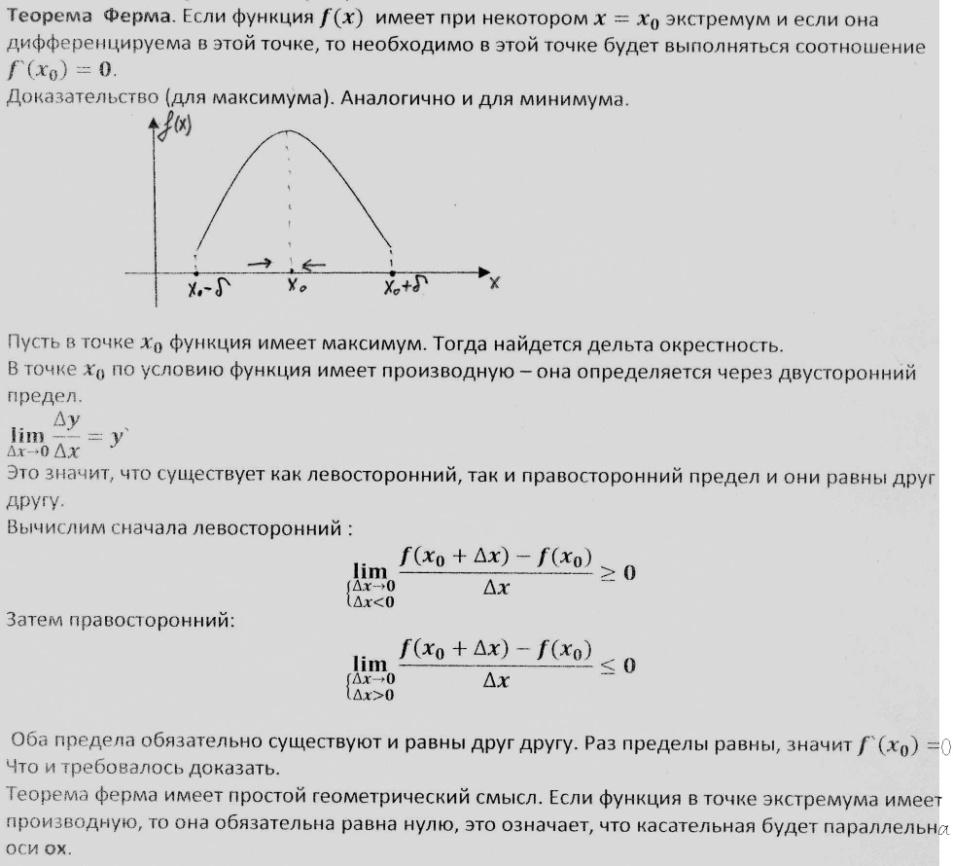
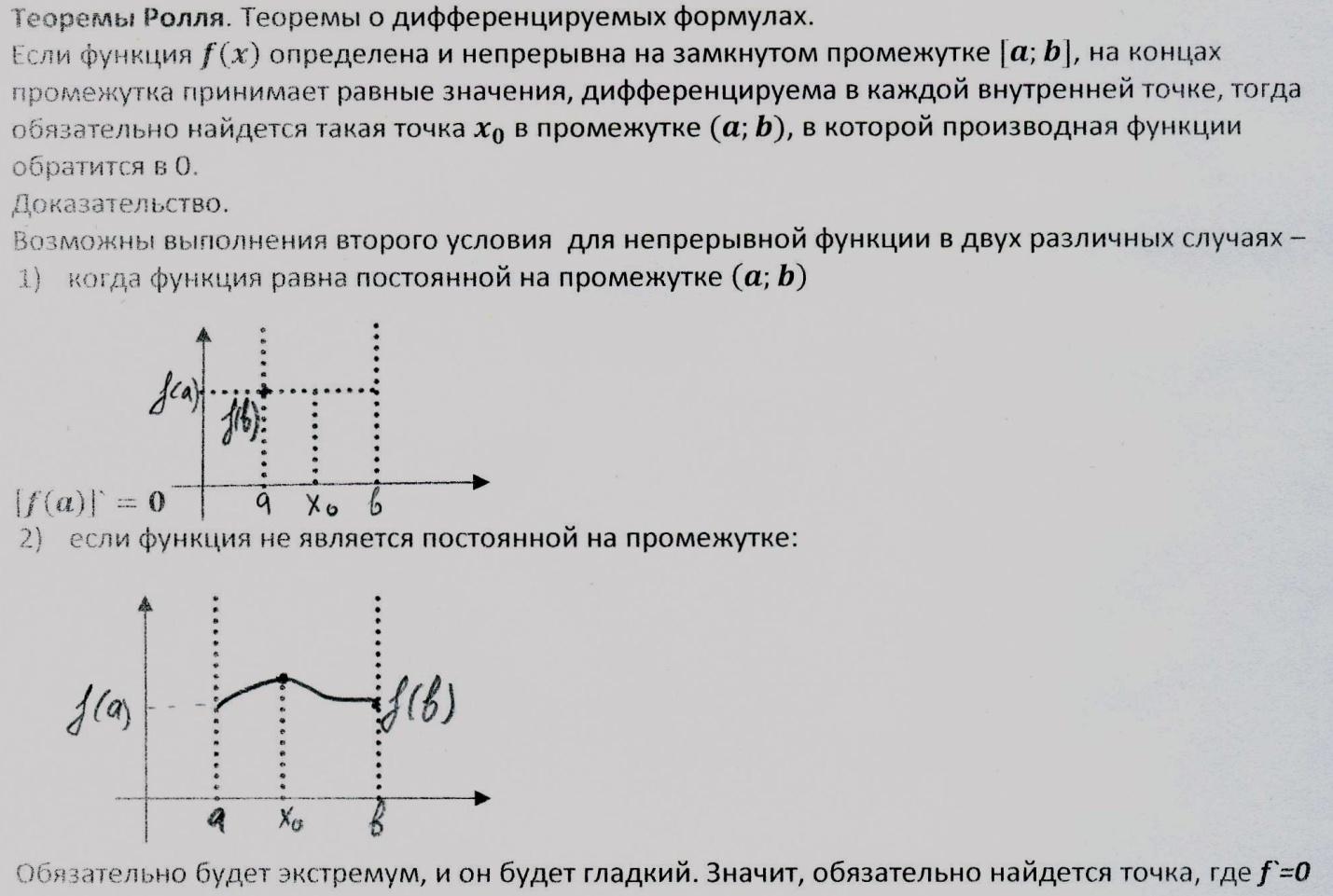
23.Теорема Ролля.
24.Теорема Лагранжа. Следствие – признак постоянства функции.

Если на некотором промежутке производная тождественно равна нулю, то функция на этом промежутке постоянна.
Доказательство. Будем понимать заданную функцию у = f(x) как закон движения материальной точки Р по оси у. Если производная обратилась в нуль, то точка Р остановилась. Если производная все время равна нулю, то точка Р все время стоит на месте, а тогда функция у является постоянной, что и требовалось доказать. Заметим, что верна и обратная теорема: если функция постоянна, то ее производная равна нулю. Производную постоянной функции мы вычислили ранее. Таким образом, f = const
25.Правила Лопиталя (без док).
Правило
Лопиталя
представляет собой метод вычисления
пределов, имеющих неопределенность
типа
![]() или
или
![]() .
Пусть a
является некоторым конечным действительным
числом или равно бесконечности.
.
Пусть a
является некоторым конечным действительным
числом или равно бесконечности.
-
Если
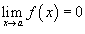 и
и
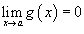 ,
то
,
то
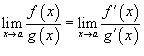
-
Если
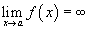 и
и
 ,
то аналогично
,
то аналогично
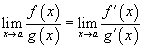
26.Монотонность функции. Необходимое и достаточное условия монотонности. Достаточное условие строгой монотонности.
Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.
Функция f (x) называется возрастающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 < x2, выполняется неравенство f (x1) < f (x2).
Функция f (x) называется убывающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 < x2, выполняется неравенство f (x1) > f (x2).
Достаточный признак монотонности.

f`(x)<0 – необходимый признак убывания функции.
Достаточное условие строгой монотонности функции на промежутке. Теорема (достаточное условие) Если функция f(x) дифференцируема на (a,b) и f/(x)≥0 (f/(x)≤0) на (a,b), то f(x) не убывает (не возрастает) на (a,b). Доказательство Рассмотрим случай когда f/(x)≥0 . Рассмотрим две точки x1,x2∈(a,b) и применим формулу Лагранжа. На [x1,x2] функция f(x) удовлетворяет всем условиям этой теоремы. Следует, чтоx1<x2: f(x2)−f(x1)=f/(c)(x2−x1), где c∈(x1,x2) и правая часть больше нуля, значит f(x2)−f(x1)≥0 или f(x2)≥f(x1) при x2>x1, функция не убывает. Теорема доказана.
27.Экстремум функции. Необходимое условие экстремума функции. Достаточное условие строгого экстремума функции (первое – перемена знака производной при переходе через исследуемую точку, второе – при помощи второй производной).
. Говорят, что функция ![]() при
при ![]() имеет минимум, если найдется такая
дельта окрестность этой точки, что для
всех x принадлежащих
этой дельта окрестности будет выполняться
условие
имеет минимум, если найдется такая
дельта окрестность этой точки, что для
всех x принадлежащих
этой дельта окрестности будет выполняться
условие ![]() .
.
![]() (
(![]() )
)
Общим названием для максимума и минимума
служит термин – экстремум. При ![]() функция имеет экстремум, если в этой
точке она имеет или максимум, или минимум.
функция имеет экстремум, если в этой
точке она имеет или максимум, или минимум.
Через производную формулируются
необходимые и достаточные условия для
того, чтобы функция в точке ![]() имела экстремум.
имела экстремум.
Необходимое условие экстремума - Если
функция ![]() имеет при некотором
имеет при некотором ![]() экстремум и если она дифференцируема
в этой точке, то необходимо в этой точке
будет выполняться соотношение
экстремум и если она дифференцируема
в этой точке, то необходимо в этой точке
будет выполняться соотношение ![]() .
.
Достаточные условия строго экстремума:

