
Тема 6. «Многочлены: теорема Безу и схема Горнера. Разложения алгебраических дробей»
Ранее понятие многочлена было определено как алгебраическая сумма одночленов. Если все подобные одночлены многочлена приведены и расположены в порядке убывания степени переменной, то полученная запись называется канонической формой записи многочлена.
Определение. Выражение вида

где
x
– некоторая переменная,
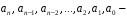 действительные
числа, причем
действительные
числа, причем
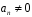 ,
называется многочленом
степени n
от переменной x.
Степенью
многочлена является наибольшая степень
переменной в его канонической записи.
Если переменная не встречается в записи
многочлена, т.е. многочлен равен константе,
его степень считается равной 0. Случай,
когда многочлен
,
называется многочленом
степени n
от переменной x.
Степенью
многочлена является наибольшая степень
переменной в его канонической записи.
Если переменная не встречается в записи
многочлена, т.е. многочлен равен константе,
его степень считается равной 0. Случай,
когда многочлен
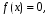 необходимо рассматривать отдельно. В
этом случае принято считать, что его
степень не определена.
необходимо рассматривать отдельно. В
этом случае принято считать, что его
степень не определена.
Примеры.
 многочлен
второй степени,
многочлен
второй степени,
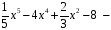 многочлен
пятой степени.
многочлен
пятой степени.
Определение. Два многочлена равны тогда и только тогда, когда у них в канонических формах при одинаковых степенях стоят одинаковые коэффициенты.
Определение.
Число
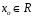 называется корнем
многочлена
называется корнем
многочлена
 ,
если при постановке этого числа вместо
x
многочлен принимает значение 0, т.е.
,
если при постановке этого числа вместо
x
многочлен принимает значение 0, т.е.
 Другими
словами,
Другими
словами,
 будет являться корнем уравнения
будет являться корнем уравнения
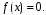
Таким образом, задача отыскания всех корней многочлена и корней рационального уравнения – одна и та же задача.
Рациональные уравнения первой и второй степени решаются по известным алгоритмам. Существуют также формулы отыскания корней многочленов третьей и четвертой степени (формулы Кардано и Феррари), однако в силу их громоздкости они не входят в курс элементарной математики.
Общей идеей отыскания корней многочленов высших степеней является разложение многочлена на множители и замена уравнения равносильной ему совокупностью уравнений более низкой степени.
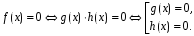
В предыдущих темах отмечались основные способы разложения многочленов на множители: вынесение общего множителя; группировка; формулы сокращенного умножения.
Однако способ группировки не носит алгоритмического характера, поэтому его трудно применять для многочленов больших степеней. Рассмотрим некоторые дополнительные теоремы и методы, позволяющие раскладывать на множители многочлены высших степеней.
Теорема
о делении с остатком.
Пусть даны многочлены
 ,
причем степень
,
причем степень
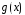 отлична от 0, и степень
отлична от 0, и степень
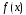 больше степени
больше степени
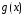 .
Тогда существуют многочлены
.
Тогда существуют многочлены
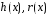 ,
такие, что выполняется равенство
,
такие, что выполняется равенство
 .
.
Причем,
степень
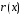 меньше степени
меньше степени
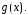 Многочлен
Многочлен
 называется делимым,
многочлен
называется делимым,
многочлен
 делителем,
многочлен
делителем,
многочлен
 неполным
частным,
а многочлен
неполным
частным,
а многочлен
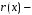 остатком.
остатком.
Если
остаток от деления равен 0, то говорят,
что
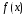 делится
на
делится
на
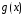 нацело,
при этом равенство принимает вид:
нацело,
при этом равенство принимает вид:
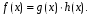
Алгоритм деления многочлена на многочлен аналогичен алгоритму деления числа на число столбиком или уголком. Опишем шаги алгоритма.
-
Записать делимое в строчку, включая все степени переменной (те, которые отсутствуют, записать с коэффициентом 0).
-
Записать в «уголке» делимое, включая все степени переменной.
-
Чтобы найти первое слагаемое (одночлен) в неполном частном, нужно старший одночлен делимого разделить на старший одночлен делителя.
-
Полученное первое слагаемое частного умножить на весь делитель и результат записать под делимым, причем одинаковые степени переменной записать друг под другом.
-
Из делимого вычесть полученное произведение.
-
К полученному остатку применить алгоритм, начиная с пункта 1).
-
Алгоритм завершен, когда полученная разность будет иметь степень меньше степени делителя. Это – остаток.
Пример.
Разделить многочлен
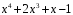 на
на
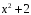 .
.
-
Записываем делимое и делитель
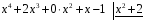
-
Находим старший одночлен частного, разделив
 на
на
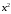 .
Умножаем его на делитель и вычитаем из
делимого.
.
Умножаем его на делитель и вычитаем из
делимого.

-
Повторяем процедуру
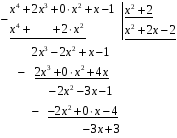
Степень
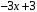 меньше степени делителя. Значит, это –
остаток. Результат деления запишется
так:
меньше степени делителя. Значит, это –
остаток. Результат деления запишется
так:
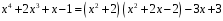
Схема
Горнера.
Если делителем является многочлен
первой степени, то процедуру деления
можно упростить. Рассмотрим алгоритм
деления многочлена
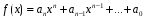 на двучлен
на двучлен
 .
.
-
Нарисовать таблицу с двумя строками и числом столбцов, равным степени делимого, увеличенной на единицу.
-
В первую строку таблицы вписать коэффициенты делимого, записанного в канонической форме, включая и нулевые коэффициенты для отсутствующих степеней x.
-
Перед началом второй строки вписать число а. В первую клетку второй строки вписать то число, которое стоит в первой клетке первой строки (старший коэффициент делимого будет и старшим коэффициентом делителя).
-
Каждая следующая клетка второй строки заполняется по правилу: предыдущее число второй строки умножается на число а, к результату прибавляется число из первой строки, стоящее в клетке с предыдущим номером.
-
В результате в клетках второй строки (кроме последней) получаем коэффициенты неполного частного, а в последней – остаток от деления. Если остаток получился 0, то исходный многочлен делится на двучлен
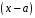 без остатка.
без остатка.
Пример.
Разделить по схеме Горнера многочлен
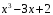 на
на
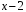 .
В этом случае а=2.
Выпишем по шагам результаты выполнения
алгоритма.
.
В этом случае а=2.
Выпишем по шагам результаты выполнения
алгоритма.
|
|
1 |
0 |
-3 |
2 |
|
2 |
1 |
|
|
|
|
|
1 |
0 |
-3 |
2 |
|
2 |
1 |
2 |
|
|
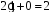
|
|
1 |
0 |
-3 |
2 |
|
2 |
1 |
2 |
1 |
|
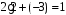
|
|
1 |
0 |
-3 |
2 |
|
2 |
1 |
2 |
1 |
4 |
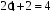
Таким образом, результат деления запишем так
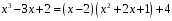 .
.
Замечание. Если необходимо выполнить деление на двучлен
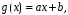 то
его преобразовывают к виду
то
его преобразовывают к виду
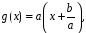 тогда
тогда
 .
Отсюда видно, что, разделив по схеме
Горнера
.
Отсюда видно, что, разделив по схеме
Горнера
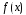 на
на
 мы найдем
мы найдем
 Тогда искомое частное
Тогда искомое частное
 получится делением найденного на а.
Остаток остается таким же.
получится делением найденного на а.
Остаток остается таким же.
Теорема
Безу.
Остаток от деления многочлена
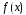 на
на
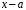 равен значению многочлена в точке x=а,
т.е.
равен значению многочлена в точке x=а,
т.е.
 .
Многочлен
.
Многочлен
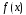 делится
на
делится
на
 без остатка тогда и только тогда, когда
x=а
является корнем многочлена
без остатка тогда и только тогда, когда
x=а
является корнем многочлена
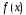 .
.
Таким
образом, найдя один корень многочлена
а,
можно его разложить на множители
 ,
выделив множитель
,
выделив множитель
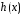 ,
имеющий степень на единицу меньше
степени
,
имеющий степень на единицу меньше
степени
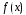 .
Найти этот множитель можно либо по схеме
Горнера, либо делением «уголком».
.
Найти этот множитель можно либо по схеме
Горнера, либо делением «уголком».
Вопрос о нахождении корня решается либо подбором, либо с использованием теоремы о рациональных корнях многочлена.
Теорема.
Пусть многочлен
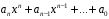 имеет целые коэффициенты. Если несократимая
дробь
имеет целые коэффициенты. Если несократимая
дробь
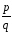 является корнем многочлена, то ее
числитель p
является делителем свободного члена
является корнем многочлена, то ее
числитель p
является делителем свободного члена
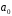 ,
а знаменатель q
является делителем старшего коэффициента
,
а знаменатель q
является делителем старшего коэффициента
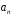 .
.
Эта теорема лежит в основании алгоритма поиска рациональных корней многочлена (если они есть).
-
Выписать все делители свободного члена.
-
Выписать все делители старшего коэффициента.
-
Составить дроби вида
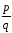 ,
удовлетворяющие условиям теоремы. Эти
числа являются «претендентами» в
рациональные корни многочлена.
,
удовлетворяющие условиям теоремы. Эти
числа являются «претендентами» в
рациональные корни многочлена. -
Подстановкой или по схеме Горнера проверяем, имеются ли среди «претендентов» корни многочлена. Если многочлен имеет рациональные корни, то они все содержатся среди «претендентов» и будут выявлены.
-
Разделить многочлен на двучлен
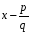 .
. -
К полученному частному можно вновь применить данный алгоритм. При этом список «претендентов» либо остается тем же, либо сокращается.
Разложение алгебраической дроби в сумму простейших дробей
Определение Дробь, в числителе и в знаменателе которой стоят многочлены, называется алгебраической дробью.
Рассмотрим
алгебраические дроби от одной переменной.
Их в общем виде можно записать так:
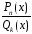 ,
где в числителе стоит многочлен степени
n,
в знаменателе – многочлен степени k.
Если
,
где в числителе стоит многочлен степени
n,
в знаменателе – многочлен степени k.
Если
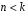 ,
то дробь называется правильной.
,
то дробь называется правильной.
К простейшим алгебраическим дробям относятся правильные дроби двух видов:
-
В знаменателе дроби стоит многочлен вида
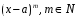 ,
а в числителе – число (многочлен нулевой
степени).
,
а в числителе – число (многочлен нулевой
степени). -
В знаменателе дроби стоит многочлен
 ,
а в числителе – многочлен первой
степени.
,
а в числителе – многочлен первой
степени.
Теорема. Любую алгебраическую дробь можно представить в виде суммы простейших алгебраических дробей.
Алгоритм разложения алгебраической дроби в сумму простейших дробей.
-
Разложить знаменатель на множители.
-
Определить количество правильных дробей и вид их знаменателей.
-
Записать равенство, в левой части которого – исходная дробь, в правой – сумма простейших дробей с неопределенными коэффициентами.
-
Привести дроби в правой части к общему знаменателю.
-
Приравнять многочлены, стоящие в числителях дробей. Пользуясь определением равенства многочленов, составить систему линейных уравнений и решить ее, найдя неопределенные коэффициенты.
-
Записать ответ.
