
FKS
.pdf1
1.Квантова теорія вільних електронів у кристалі.
Квантова теорія вільних електронів базується на тих же відомих експериментальних даних з властивості металів, що і класична теорія (велика електрота теплопровідність металів, збільшення електричного струму зі збільшенням температури та ін.). Але спосіб опису електронів в цій теорії був принципово інший в порівнянні з класичною теорією. Стан електрона описувався за допомогою хвильової функції, а розподіл колективізованих зовнішніх електронів за станами, визначався законами квантової статичної фізики
Хвильова функція вільних електронів
Хвильову функцію вільних електронів в кристалі треба знаходити з рівняння Шредінгера для стаціонарного стану, тобто коли потенціальна енергія
U (r) 0 .
Рівняння Шредінгера:
(2-1)
де, ∆ - оператор Лапласса;
(r) - хвильова функція вільного електрону;
ħ – стала Планка; m – маса електрона;
Е– енергія (кінетична).
Водновимірному випадку рівняння має вигляд:
(2-2)
Позначимо вираз:
(2-3)
Параметр к пов’язаний з енергією електрона і від нього залежить хвильова функція. Він відіграє дуже важливу роль в квантовій теорії твердого тіла(2.
d-4)
Знайдемо розв’язок рівняння (2-4). Розв’язок цього рівняння має вигляд:
-5)
де, r1, r2 – корні характерного рівняння:
-6) -7)
-8)
де, і = √-1
Тоді загальний розв’язок рівняння буде мати вид:
r-9)
Індекс k в рівнянні (2-9) ми пишемо тому, що хвильова функція залежить від k, як від параметру. Окремі розв’язки:
-10) -11)

2
В результаті цих розрахунків можна зробити висновок:
вільний електрон в кристалі може перебувати в трьох станах з хвильовими функціями (2- 9), (2-10), (2-11).
Графічно хвильова функція може бути представлена, як плоска хвиля, що поширюється
|
|
у напрямку осі ох. |
|
|
|
|||
|
|
Фізична суть параметра k |
|
|||||
|
|
|
|
Оскільки, E |
m 2 |
, то |
||
|
|
|
|
2 |
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
2mm 2 |
2mp2 |
p2 |
-12) |
||
|
k |
|
2 2 |
2 2m |
2 |
|||
|
|
|
||||||
|
|
|
|
|
|
|
|
-13) |
|
|
|
|
|
|
|
|
-14) |
Таким чином з одного боку параметр k пропорційний імпульсу вільного електрона. |
||||||||
З іншого боку: |
|
|
|
|
|
|
|
|
|
k p m |
2 |
|
|
-15) |
|||
|
|
|
|
|||||
|
|
|
|
h |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
h |
- формула Де Бройля |
|
|
|
-16) |
|||
m |
|
|
|
|
|
|
|
|
k 2



 (2
(2
Це відоме в теорії оптичних явищ, як хвильове число, яке вказує скільки разів довжина
хвилі даного хвильового процесу вміщується у відрізку 2 .
У тривимірному випадку розв’язок рівняння Шредінгера буде мати вигляд:
(3-1)
Оскільки енергія електрона пов’язана з параметромkза формулою (3-3) і оскільки можливі будь-які значення k, то можливі і будь-які значення Е. Зобразимо графік залежності енергії Е електрона від параметра k:
(3-2)
де, r - радіус вектор будь-якої точки простору в кристалі
k - вектор з координатами kx , ky , kz .
Можливі значення енергії електрона визначаються властивостями хвильової функції. З виду хвильової функції (2-9), (3-1), (3-2) витікає, що при будь-яких значеннях параметра к, ця
хвильова функція однозначна, кінцева та неперервна.
(3-3)
Таким чином робимо висновок: що енергетичний спектр вільної частини неперервний і має вигляд параболи.
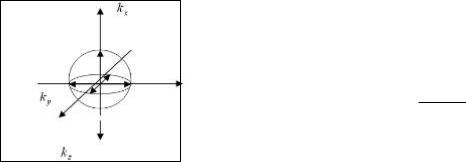
3
2. Поверхня Фермі вільних електронів у кристалі.
Кожний квантовий стан вільного електрона в кристалі задається вектором k оскільки цей стан визначається хвильовою функцією:
|
|
|
|
|
k |
(r ) c ei(k ,r ) . |
|||
|
|
|
|
|
У кожному такому стані у відповідності з принципом Паулі можуть знаходитись два електрони з протилежно зорієнтованими спінами.
Розподілення електронів за станами при низькій температурі, визначається тим що енергія всієї системи повинна бути мінімальною. Тому при проведенні уявного експерименту, додаванні вільних електронів до кристалічної гратки електрони будуть займати мінімальну енергію яка тільки можлива згідно з принципом Паулі.
k x
k y k z
k простір – це область визначення вектора k з системою координат де є осі kx , k y , kz .
Якщо до ядра додавати електрони то перші два електрони
будуть мати вектор k 0
E 2 k 2 0 .
2m
|
|
|
|
Якщо додати ще два електрони то (нехай для нашого |
||||||||||
|
|
|
|
експерименту: n n1 |
n2 |
n3 , |
a a1 a2 a3 ): |
|||||||
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
n |
(4-1). |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
a |
n |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Якщо додати ще два електрони:
k x |
0 |
|
|
|
||
k y |
2 |
|
1 |
|
(4-2). |
|
|
|
|
||||
a |
n |
|||||
|
|
|
|
|||
k z |
0 |
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
k x |
|
|
(4-3). |
|
|
|||||
k y |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
k z |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a |
|
|
|
|
|
|
|
|||
Наступні два електрони: |
|
|
|
|
|
|
|
|
|
|
Наступні два електрони: |
|
|
|
|
|
|
|
|
|
|
|
k x |
|
2 |
|
1 |
|
||||
|
|
|
|
|
(4-3). |
|||||
|
|
|
|
|
|
a |
n |
|||
|
|
|
|
|
|
|
||||
|
|
|
k y |
0 |
|
|
|
|||
|
|
|
k z |
0 |
|
|
|
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Крім перших двох у наступних 12 електронів енергія буде однакова, оскільки довжина
вектора k у цих електронів буде однакова.
З цієї стадії експерименту витікає, що вектори k які задають стани електронів з
однаковою енергією обмежено сферою радіус якої дорівнює k .
Тому можна зробити висновок, що точки в k просторі, які зображають квантові стани з однаковою енергією лежать на поверхні сфери певного радіуса для даного випадку:

k |
2 1 |
; |
||
|
|
|
|
|
|
|
a n |
|
|
|
|
|
||
Наступні два електрони будуть мати k - вектор з складовими:
k x |
|
2 |
|
|
1 |
||
a |
n |
|
|||||
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
k y |
|
|
|
1 |
|||
|
|
|
|
||||
|
|
|
|||||
|
k z |
a |
|
|
n |
||
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Довжина цього вектора буде дорівнювати по теоремі Піфагора:
4
(4-5).
|
k |
|
|
|
|
|
(4-6). |
||
|
2 2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a n |
|
|
|||
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
Наступні електрони будуть мати більше значення вектора k |
і довжину вектора. Всі |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
електрони з вектором довжини |
k |
|
будуть мати однакову енергію і кінці векторів |
|||||||||||
|
a n |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k будуть лежати на поверхні другої сфери. |
|
|
|
|
|
|
|
|||||||
Розглядаючи таким чином всі інші можливі стани електронів, можна прийти до висновку: |
||||||||||||||
|
|
|
|
|
|
|
|
|
2 max |
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
kmax |
|
|
|
|
|
|
(4-7); |
||
|
|
|
|
|
|
|
|
a n |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 |
k 2 |
|
|
|
|
|
|
|
|
Emax |
|
|
max |
|
(4-8). |
||||
|
|
|
|
|
|
|
2m |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
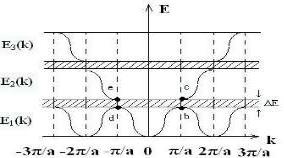
Область в k - просторі в межах якої точки, що зображують зайняті електронні стани при |
||||||||||||||
абсолютному нулі температур являють собою сферу. Поверхня цієї сфери радіус якої дорівнює
|
|
|
|
2 max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
kmax |
|
|
|
|
називається поверхнею Фермі. |
|
|
|
||
|
a n |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Максимальна енергія зайнятих електронами станів називається енергією Фермі: |
|
|||||||||
|
|
|
|
|
|
Emax |
2 |
k 2 |
|
|
|
|
|
|
|
|
|
max |
|
(4-8). |
|
|
|
|
|
|
|
|
2m |
|||
|
|
|
|
|
|
|
|
|
||
5
3.Зони Бріллюена.
Враховуючи два наслідки з теореми Блоха побудуємо залежність Е(k) для електрона в
періодичному полі кристалічної гратки для зон, що не перекриваються в одновимірному випадку:
1) В межах першої зони Е1, при k=0. E1(k) повинна
бути min, оскільки при U →0: E |
|
|
h2k 2 |
. Тоді при |
k |
|
|||
x |
|
2m |
|
|
|
|
|
|
k=0, E=Emin=0. Функція Е1(k) в точці k дорівнює 0. Функція Е1(k), а також Еі(k) повинна бути
парною функцією від k, т.б. графік функції Еі(k) симетричний відносно осі ординат.
E(k)=E(-k) (6.3)
2) Min вектор оберненої гратки пов’язаний з періодом кубічної гратки формулою: |b|=|1/a| (6.4). Тоді період з яким буде змінюватись енергія електрона |2πb|=2π/a (6.5).
Функція E1(k)=0 в точках: 2π/a, 4π/a, ..., -2π/a, -4π/a,...буде дорівнювати нулю.
Точки π/a=k та k’= -π/a відстають одна від одної на відстані 2π/a, тому значення Е1(k) в цих точках повинно бути однакове. В цих точках мають бути max значення функції Е1(k).
Як витікає з побудови в 1-й енергетичній зоні функція Е1(k) має перші max в точках ±π/a, в
цих точках dE/dk=0 (6.6), d2E/dk2<0 (6.7)
Побудована крива періодично повторюється при збільшенні та зменшенні k. Оскільки нас цікавлять стани, які фізично розрізняються (стани в яких можуть знаходитись електрони в 1-й зоні), то функцію Е1(k) необхідно розглядати на інтервалі [-π/a; π/a]. Цей відрізок це зона значень хвильового вектора k, яка визначає можливі електронні стани з енергіями Е1(k). Цей відрізок хвильового вектора k називають першою зоною Бріллюена, її межами є точки з координатами -π/a, π/a, які відповідають числам k, k’. Ці числа зв’язані формулою k-2π/a=k’ (6.8), k’+2π/a=k (6,9). Формули (6.8), (6.9) визначають межі першої зони Бріллюена в одновимірному випадку. Якщо вважати вісь k вісью kx, тоді k=iπ/a, k’= -iπ/a.
k=k’- 2πb(100) (6.10)
Розглянемо 2-гу енергетичну зону і функції Е2(k), оскільки Ux→0, ΔE→0 і залежність Е(k) перетворюється на параболу і в цьому випадку b з c, d з e. Тобто max Е1(k)÷min Е2(k). Значення енергії другої енергетичної зони електрон може мати лише в тому випадку коли k, яке визначає його стан лежить в межах [-π/a; π/a], ці ділянки осі k називаються другою зоною Бріллюена, межі другої зони Бріллюена визначаються формулами: k=i2π/a, k’= -i2π/a (7.1) (і – одиничний вектор (від i,j,k))
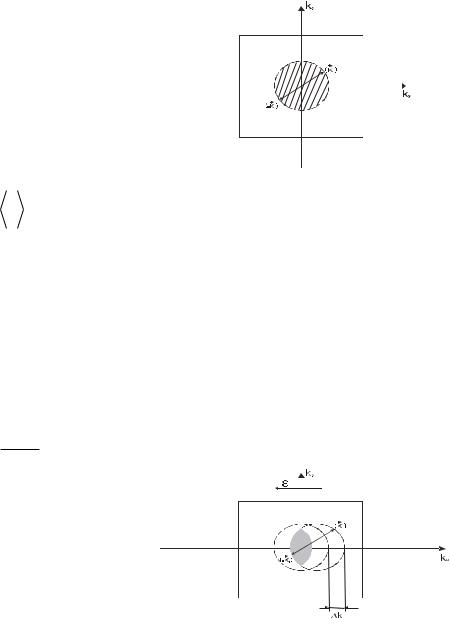
Повторюючи ці міркування для третьої енергетичної зони а токож більш високих, приходимо до висновку, що залежність енергії від хвильового вектору k, для енергетичних зон, що не перекриваються, буде мати вигляд, що зображено на малюнку. Всі міркування наведені для одновимірного простору залишаються в силі і для об’ємного простору, якщо вважати,що k по черзі kx, ky, kz, та a: ax, ay, az. Тоді формули, що визначають межі зони Бріллюена матимуть вигляд:
k=k’+ 2πb (7.2) |k|=|k’|
Висновки: Можливі значення енергії електрона в періодичному полі кристалічної гратки лежать в межах енергетичних зон Е1, Е2,... Якщо зони не перекриваються, між ними утворюються зони заборонених енергій. Всі значення хвильового вектора k які відповідають дозволені значення енергії утворюють області в k-просторі, що називаються зонами Бріллюена. Кожна з зон Бриллюена це зона в k-просторі, в межах якої знаходяться всі хвильові вектори, які визначають фізично відмінні стани електронів з енергіями в межах певної (відповідної) енергетичної зони. Межі зони Бріллюена це геометричне місце точок в k-просторі, які

6
відповідають розривам неперевності функції Е(k). Ступінь заповнення електронних станів зон Бріллюена електронами визначають багато важливих властивостей твердих тіл. Тому межі побудови зони Бріллюена та підрахунок можливих станів дуже важливі
4. Провідники з точки зору зонної теорії.
Розглянемо тверде тіло, у якого перша зона Бріллюена зайнята неповність. Це може бути метал (одновалентний) у якого зона заповнена наполовину.
Заповнені стани будуть мати вигляд сфери розташованої симетрично відносно початку координат.
Всі електрони в кристалі мають середню швидкість:
|
|
1 |
|
|
|
|
|
|
|
|
E |
(8-1) |
|
|
|
k
d ( k) |
0 |
(8-11) |
|
dt |
|||
|
|
Результуючого переносу заряду в кристалі не буде, оскільки кожному електрону, який
|
|
визначається k i , відповідає електрон (- k i ).
Якщо прикласти до кристала електричне поле з напруженістю буде діяти сила:
|
|
F |
e |
Якщо на електрон діє сила F , то виконується умова:
d ( k) F
dt
, то на кожний електрон
(10-1)
(8-10)
і всі k i отримують приріст в напрямку осі kx. Тобто весь розподіл в зоні Бріллюена заповнених зон зміститься вздовж осі kx на відстань k:
k F

7
Оскільки розподіл несиметричний відносно осі ky, то в цьому випадку буде результуючий перенос заряду в напрямку осі х.
Таким чином, речовини у яких неповністю зайнята перша зона Бріллюена, є провідниками електрики.
5. Діелектрики з точки зору зонної теорії.
Розглянемо тверде тіло, у якого перша зона Бріллюена зайнята неповність. Це може бути метал (одновалентний) у якого зона заповнена наполовину.
Заповнені стани будуть мати вигляд сфери розташованої симетрично відносно початку координат.
Всі електрони в кристалі мають середню швидкість:
|
|
1 |
|
|
|
|
|
|
|
|
E |
(8-1) |
|
|
|
k
d ( k) |
0 |
(8-11) |
|
dt |
|||
|
|
Результуючого переносу заряду в кристалі не буде, оскільки кожному електрону, який
|
|
визначається k i , відповідає електрон (- k i ).
Якщо прикласти до кристала електричне поле з напруженістю , то на кожний електрон буде діяти сила:
|
|
|
F |
e |
(10-1) |
Якщо на електрон діє сила F , то виконується умова:
d ( k)
dt
F (8-10)
і всі k i отримують приріст в напрямку осі kx. Тобто весь розподіл в зоні Бріллюена заповнених зон зміститься вздовж осі kx на відстань k:
k F
Оскільки розподіл несиметричний відносно осі ky, то в цьому випадку буде результуючий перенос заряду в напрямку осі х.
8
Якщо вмістити в електричне поле речовину, у якої повністю зайнята перша зона
Бріллюена і досить велика зона заборонених значень Е, то розподіл k i не зможе зміщуватися і така речовина називається діелектриком.
6. Напівпровідники з точки зору зонної теорії.
Розглянемо тверде тіло, у якого перша зона Бріллюена зайнята неповність. Це може бути метал (одновалентний) у якого зона заповнена наполовину.
Заповнені стани будуть мати вигляд сфери розташованої симетрично відносно початку координат.
Всі електрони в кристалі мають середню швидкість:
|
|
1 |
|
|
|
|
|
|
|
|
E |
(8-1) |
|
|
|
k
d ( k) |
0 |
(8-11) |
|
dt |
|||
|
|
Результуючого переносу заряду в кристалі не буде, оскільки кожному електрону, який
|
|
визначається k i , відповідає електрон (- k i ).
Якщо прикласти до кристала електричне поле з напруженістю , то на кожний електрон буде діяти сила:
|
|
|
F |
e |
(10-1) |
Якщо на електрон діє сила F , то виконується умова:
d ( k)
dt
F (8-10)
і всі k i отримують приріст в напрямку осі kx. Тобто весь розподіл в зоні Бріллюена заповнених зон зміститься вздовж осі kx на відстань k:
k F
Оскільки розподіл несиметричний відносно осі ky, то в цьому випадку буде результуючий перенос заряду в напрямку осі х.

9
Напівпровідники – це речовини, які займають проміжний стан між провідниками і діелектриками. Перша зона Бріллюена у них заповнена неповністю, а зона заборонених значень досить мала і тому при підвищені температури, частина електронів переходить з першої в другу зону і поводить себе, як електрони провідності.
7. Теорема Блоха.
Теорема Блоха:
Хвильову функцію електронів у періодичному полі кристала можна представити у такому вигляді:
|
|
|
|
|
|
|
|
|
(r ) const ei(k r ) U (r ) |
(5-4). |
|||||
|
k |
|
|
|
|
k |
|
|
|
|
|
|
|
|
яка має |
k - вектор має розміри обернені довжині функції |
U (r ) . |
U (r ) -деяка функція, |
|||||
періодичність гратки. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
U |
(r ) U |
(r |
R) |
|
|
(5-5). |
|
k |
k |
|
|
|
|
|
|
Конкретний вид цієї функції невідомий, але використовуючи ф-ли (5-4) та (5-5) можна отримати всі основні висновки сучасної фізики твердого тіла.
Функція (5-5) U k (r ) називається
модулюючим множником.
Хвильова функція, яка визначається ф- лою (5-4) називається хвильовою ф-цією
Блоха.
Вона являє собою плоску хвилю
модульовану в такт гратки.
Вектор k називається хвильовим вектором
вкристалі.
8.Наслідки теореми Блоха.
1.Стани електрона в кристалі: ψк(r) та ψk+2πb(r) в межах однієї енергетичної зони фізично еквівалентні:
ψк(r)= ψk+2πb(r) |
(6.1), |
де b - вектор оберненої гратки.
тобто хвильовий вектор k електрона в періодичному полі кристалічної гратки визначений з точністтю до довільного вектора оберненої гратки домноженого на 2π
2. В межах кожної енергетичної зони енергія електрона в кристалі є періодичною функцією хвильового вектора k з періодом 2πb.
9. Циклічні умови Борна-Кармана.
Якщо розміри кристалу в якому знаходяться електрони досить великі, то явища на його поверхні практично не будуть впливати на стан електрона в центрі кристала. Мінімальний об’єм, починаючи з якого виконується вище наведена умова називається основною областю кристалу (V0). Тоді вірним буде таке твердження:
в кристалі будь-якого об’єму більшому ніж V0, фізичні стани електронів повторюються у просторі з періодом, що дорівнює лінійній величині області V0. Це можна довести, якщо з’єднати декілька областей V0 кристалів. Це твердження справедливе, як для полікристалів так і
10
для монокристалів. Експериментальні дані показують, що лінійний розмір основної області має порядок величини 10-6 м.
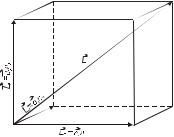
Дамо математичне формулювання циклічних умов Борна-Кармана. Представимо основну область у вигляді паралелепіпеда:
де, n1, n2, n3 – цілі числа порядка 104
a1 , a 2 , a - базисні вектори кристалічної гратки
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
L1 |
L2 |
L3 - діагональ паралелепіпеда |
|
|
|
|
(3-4) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Властивість періодичності функції (r) |
можна записати: |
|
|||||||||||||||||
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3-5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3-6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3-7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3-8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3-9) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3-10) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3-11) |
Умови (3-10), (3-11) виконуються при значеннях: |
|
|
|
|
|
||||||||||||||
|
|
|
k |
x |
n a |
|
2 |
1 |
1 |
0, 1, 2... |
|
||||||||
|
|
|
|
|
1 1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
k y |
n2 a2 |
|
2 2 |
2 |
0, 1, 2... |
(3-12) |
||||||||||
|
|
|
|
|
|
|
e |
||||||||||||
|
|
|
k |
z |
n a |
3 |
|
2 |
3 |
3 |
0, 1, 2... |
|
|||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||
З (3-12) витікає: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
kx |
|
|
2 |
|
|
1 |
|
|
|
|
|
|
||||
|
|
|
|
a1 |
|
n1 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
k y |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
a2 |
|
n2 |
|
|
|
|
(3-13) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kz |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a3 |
|
|
n3 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Формули (3-13) визначають можливі значення |
складових хвильового |
вектора k |
|||||||||||||||||
електрона в кристалі. Оскільки а1, а2, а3 та n1, n2, n3 |
фіксовані для даного кристалу числа, то |
||||||||||||||||||
