4.2. Порядок выполнения работы

1. Измерить сопротивление n резисторов одного номинала прибором Щ 4313 в режиме омметра. Результаты наблюдений занести в табл. 4.1.

2. Предполагаем, что измеряемые значения R_i подчиняются нормальному закону распределения. Последовательность обработки результатов проводить в соответствии с методикой, изложенной в ГОСТ 8.207–76:

2. Вычислить среднее арифметическое значение измеряемой величины

2. Вычислить разности между результатами отдельных наблюдений R_i и среднего значения – случайное отклонение результата наблюдения . Значение_i занести в табл. 4.1. Определить сумму всех погрешностей .

При большом числе измерений сумма случайных погрешностей стремится к нулю . Этот вывод основывается на аксиоме случайности теории случайных погрешностей, что при очень большом числе измерений и при отсутствии систематических_С погрешностей, положительные и отрицательные погрешности встречаются одинаково часто.

2. Рассчитать величины квадрата абсолютной погрешности , результаты занести в табл. 4.1.

Таблица 4.1

№	Измеренное значение Ri, Ом, кОм, МОм	Абсолютная погреш-ность измерения	Квадрат абсолютной погрешности
1
2
3
…	…	…	…
n
	Среднее арифметическое значение сопротивлений	Сумма абсолютных погрешностей	Сумма квадратов абсолют-ных погрешностей

Сумма квадратов случайных погрешностей должна быть минимальной . Такой вывод основывается на аксиоме распределения, что при большом количестве измерений малые погрешности встречаются чаще, чем большие; очень большие погрешности практически не встречаются.

2. Определить оценку среднеквадратического отклонения результатов каждого из n одноразовых наблюдений .

2. Исключить аномальные результаты (грубые промахи) по критерию «трех сигм». Для этого из ряда значений _i найти наибольшие и сравнить их с . Такой критерий надежный при числе измерений. Если, то подозреваемый в аномальности результат_max исключить, а затем повторить сначала расчеты по пунктам 2.1. – 2.4.

2.6 Найти оценку ско среднего арифметического значения .

2. Определить доверительные границы случайной составляющей погрешности и записать результат измерений. Если за результат измерений принято среднее значение , то

При Р_дов = 0,997 z_гр = 3 и .

При любой другой доверительной вероятности Р_дов можно воспользоваться табличным (или из графика) значением интервала вероятности Ф(z) = Р_дов, по его значению можно найти z_гр и далее, так как , можно определить_гр и записать результат

2. В случае, если число измерений n мало , то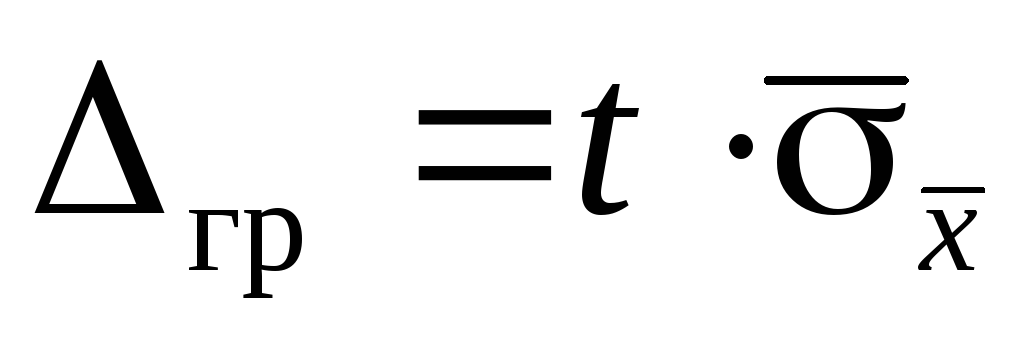, гдеt – коэффициент Стьюдента, который определяют из табличных данных при заданных Р_дов и количестве (n) наблюдений.

2. Учитывая, что систематическая погрешность _С вошла в состав результата измерений , необходимо определить доверительные границы неисключенной систематической погрешности. В качестве _С используют погрешность средства измерения

,

где  – класс точности прибора, %.

Для прибора Щ 4313 относительная погрешность определяется по формуле:

,

где a и b – коэффициенты, зависящие от конечного значения шкалы R_к.

Согласно паспортным данным прибора Щ4313, при R_к = 500 Ом, a = b = 1,5. При R_к = 5 кОм и более, a = b = 0,5.

Абсолютная погрешность: .

В случае, если , то неисключенной систематической погрешностью пренебрегают и принимают = _гр; если , то пренебрегают случайной погрешностью и считают, что = _С. В случае равенства 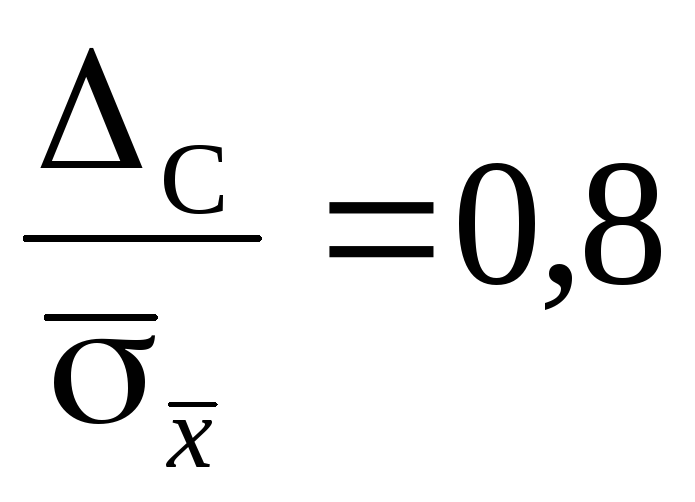вычисляют,, и тогда, а результат представляют в виде:

Числовое значение результата измерения должно заканчиваться цифрой того же порядка, что и значение погрешности . При этом число значащих цифр при определении  не должно превышать двух.

3. Определить закон распределения погрешностей результатов измерений.

Для идентификации закона распределения необходимо построить

гистограмму (рис. 4.5). Для этого весь диапазон _i разбивают на m одинаковых интервалов. Значение m должно быть нечетным (m = 9 … 13).

Рисунок 4.5 – Гистограмма

Ширину интервала определяют по соотношению:

,

где _max, _min – соответственно наибольшее и наименьшее значение погрешности _i; m – количество интервалов.

Затем подсчитывают вероятность нахождения случайной погрешности в j интервале

,

где j – 1, 2, …, m; n_j – число погрешностей, которые попадают в j-ый интервал;

n – число всех измерений.

Если погрешность попадает на границу интервала _j, то ее можно отнести либо к j-му интервалу, либо к (j+1)-му интервалу, т.е. она учитывается только один раз.

По оси результатов наблюдений откладывают интервалы _j в порядке нарастания номеров и на каждом интервале строится прямоугольник высотой (средняя плотность в интервале_j = d).

В этом случае площадь под гистограммой будет равна единице. Полученную гистограмму аппроксимируют кривой и делают выводы о законе распределения.

Как способ оценки близости распределения выборки экспериментальных данных к принятой аналитической модели закона распределения используется критерий согласия. Наибольшее распространение в практике получил критерий Пирсона.

3. Приравняв энтропию распределения, представленного гистограммой, к энтропии равномерного закона, получим энтропийное значение случайной погрешности _Э (см. рис. 4.6). При этом равенство энтропий Н_гист() = Н_равн() создает одинаковое дезинформирующее действие погрешности на измеряемую величину.

Н_гист() = Н_равн() = ln(2_Э).



Рисунок 4.6 – Распределение случайной погрешности

С учетом полученного значения _Э результат измерения сопротивления R запишем в виде:

3. Приравняем энтропию распределения, представленного гистограммой, к энтропии нормального закона:

Вычислим СКО:

Энтропийный интервал:

Используя рассчитанное значение , можно построить график () нормального закона распределения по известной формуле .

Площадь под кривой () и площадь всех столбцов гистограммы должны быть одинаковыми. Для наглядности сравнения кривую () нормального закона распределения необходимо совместить с рисунком гистограммы (см. рис. 4.7.).



Рисунок 4.7 – Нормальный закон распределения случайной погрешности