
Лабораторні роботи 1-го семестру
Лабораторна робота №1
ОБЧИСЛЕННЯ ФУНКЦІОНАЛЬНИХ РЯДІВ
Для ряду
f(x)=![]() обчислити
його наближене значення при х[0,1]
з кроком h=0.05.
Обчислення припинити, якщо |ai|<=0.001
для двох послідовних членів ряду. Задане
точне значення ряду fточ(х).
Вивести кількість ітерацій N(x,),
при яких була досягнута точність .
Побудувати таблицю такої структури:
обчислити
його наближене значення при х[0,1]
з кроком h=0.05.
Обчислення припинити, якщо |ai|<=0.001
для двох послідовних членів ряду. Задане
точне значення ряду fточ(х).
Вивести кількість ітерацій N(x,),
при яких була досягнута точність .
Побудувати таблицю такої структури:
х |
f(x) |
fточ(х) |
|
N |
|
|
… |
|
|
Побудувати на одному полі графіки функцій y=f(x), y=fточ(x). Для х=0.5 побудувати графік аi(i). Варіанти завдань:
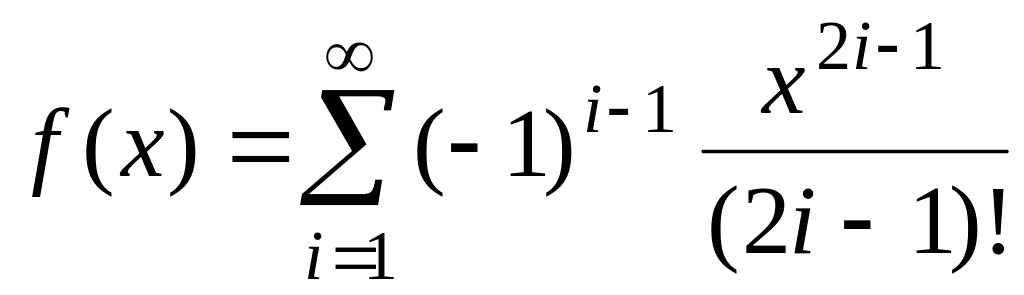 ,
fточ(х)=sin(x).
,
fточ(х)=sin(x).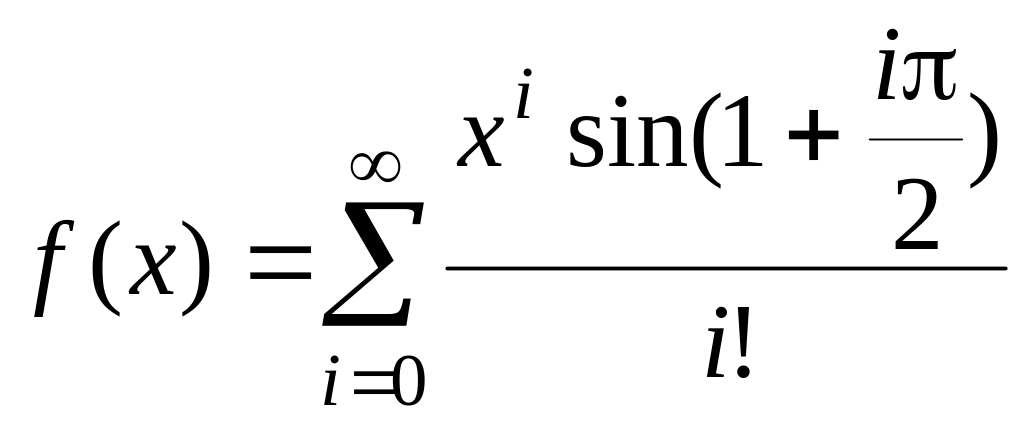 ,
fточ(х)=sin(x+1).
,
fточ(х)=sin(x+1). ,
fточ(х)=cos(x).
,
fточ(х)=cos(x). ,
fточ(х)=cos(x+1).
,
fточ(х)=cos(x+1).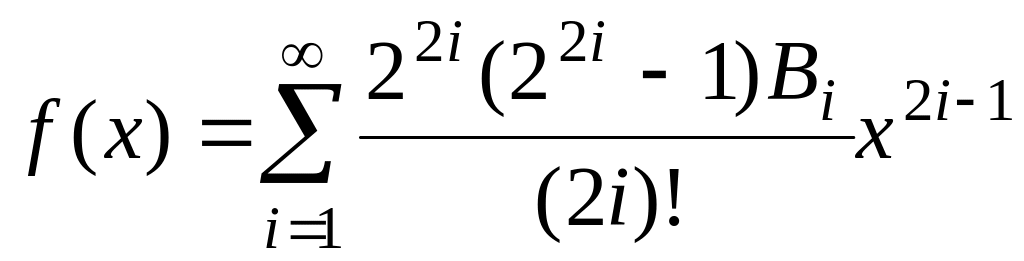 ,
де Ві
–
числа Бернуллі, fточ(х)=tg(x).
,
де Ві
–
числа Бернуллі, fточ(х)=tg(x). ,
де Ві
–
числа Бернуллі, fточ(х)=ctg(x).
,
де Ві
–
числа Бернуллі, fточ(х)=ctg(x). ,
де Еі
–
числа Ейлера, fточ(х)=sec(x).
,
де Еі
–
числа Ейлера, fточ(х)=sec(x).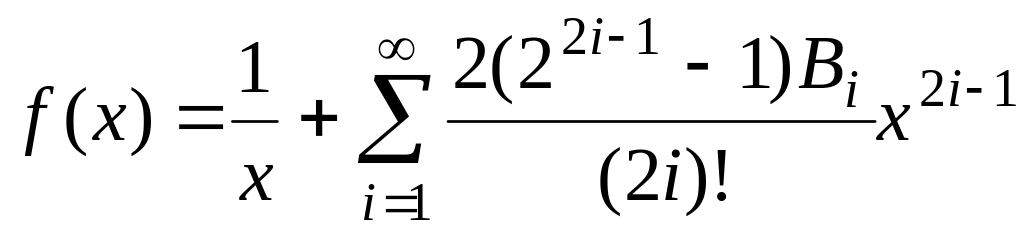 ,
де Ві–числа
Бернуллі, fточ(х)=cosec(x).
,
де Ві–числа
Бернуллі, fточ(х)=cosec(x).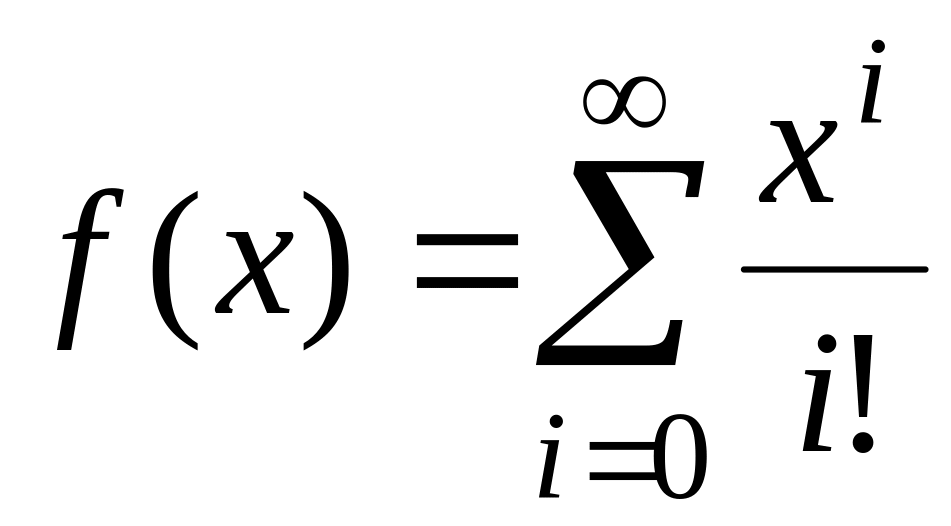 ,
fточ(х)=ex.
,
fточ(х)=ex.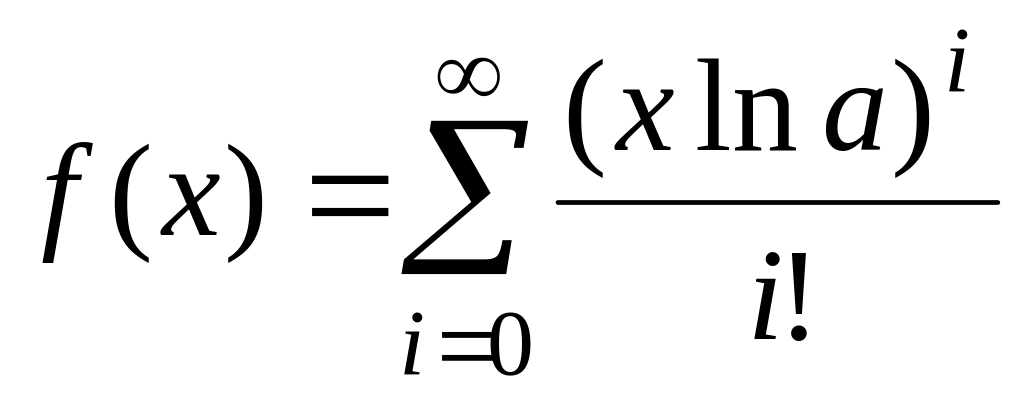 ,
fточ(х)=ax=exlna.
,
fточ(х)=ax=exlna.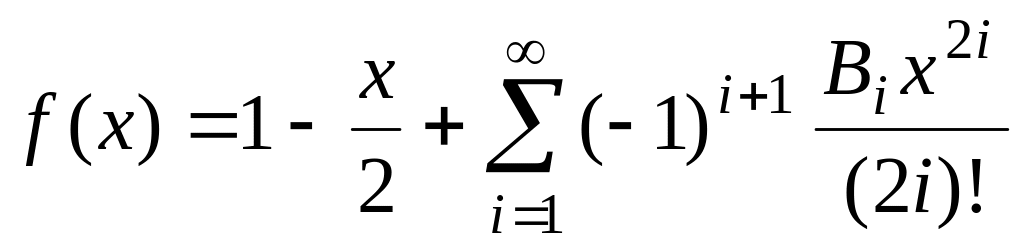 ,
де Ві
–
числа Бернуллі, fточ(х)=
,
де Ві
–
числа Бернуллі, fточ(х)=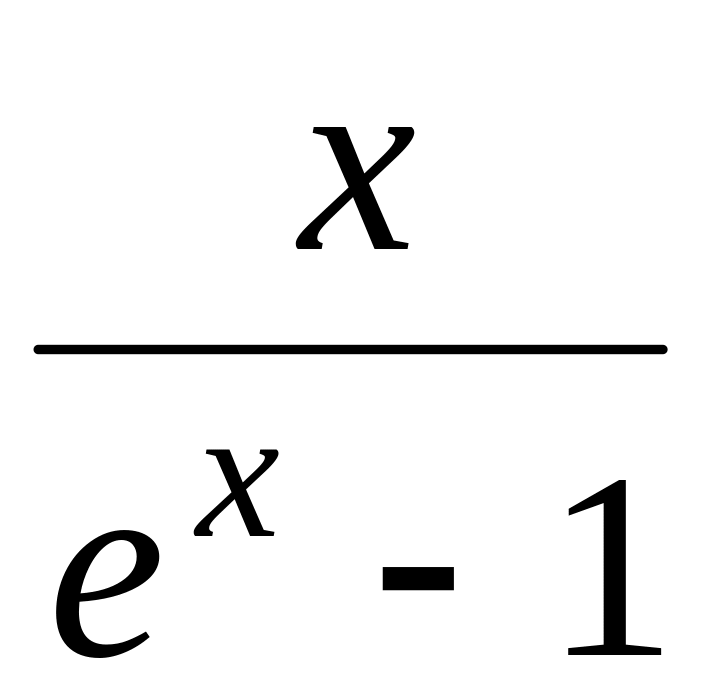 .
. ,
fточ(х)=ln(x).
,
fточ(х)=ln(x).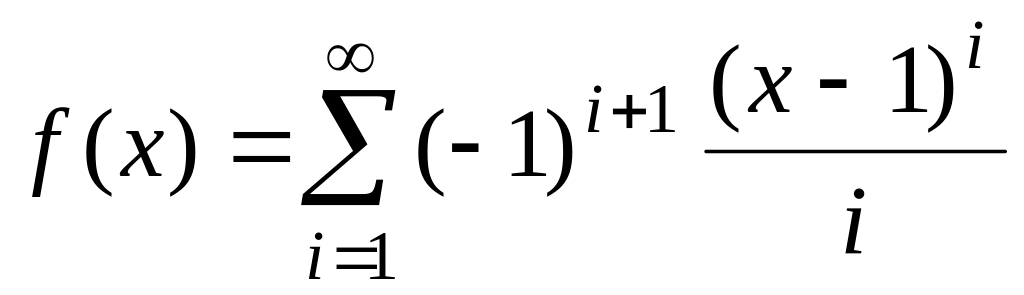 ,
fточ(х)=ln(x).
,
fточ(х)=ln(x).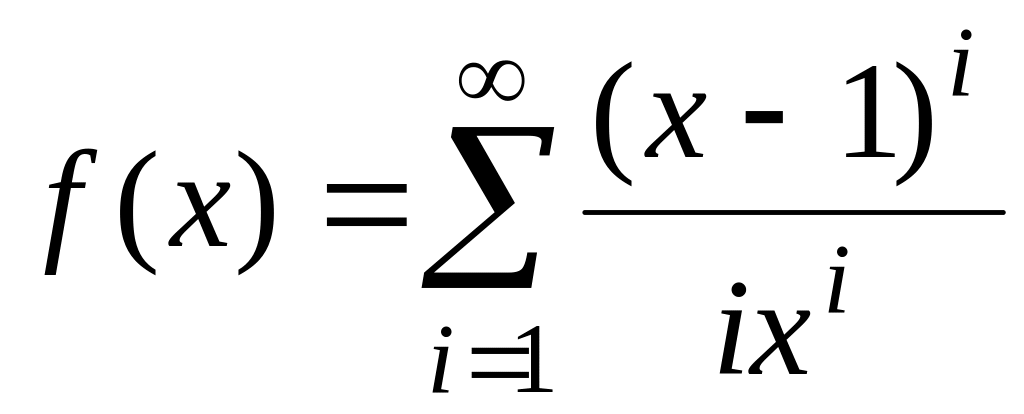 ,
fточ(х)=ln(x).
,
fточ(х)=ln(x). ,
fточ(х)=ln(x+1).
,
fточ(х)=ln(x+1).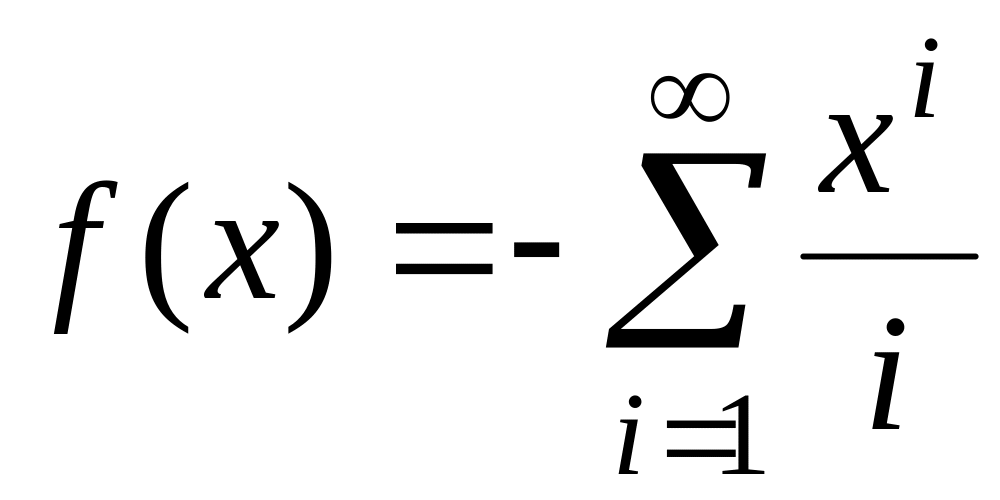 ,
fточ(х)=ln(1-x).
,
fточ(х)=ln(1-x).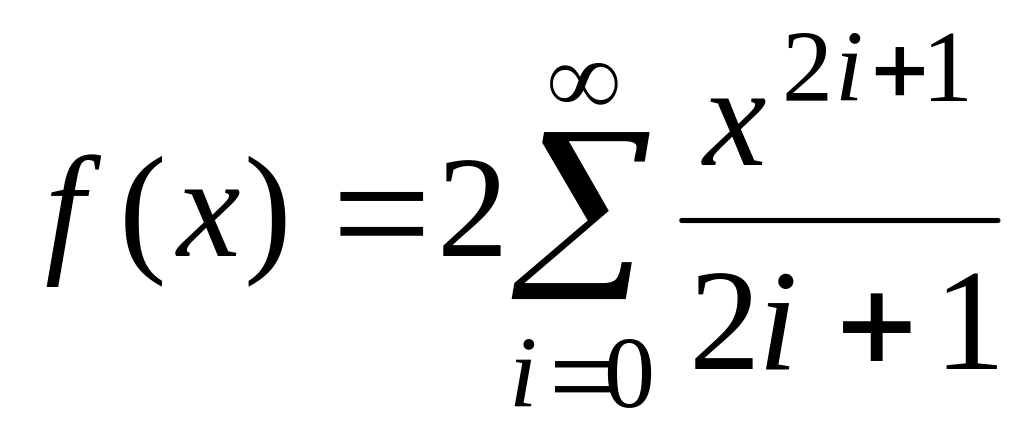 ,
fточ(х)=ln
,
fточ(х)=ln .
.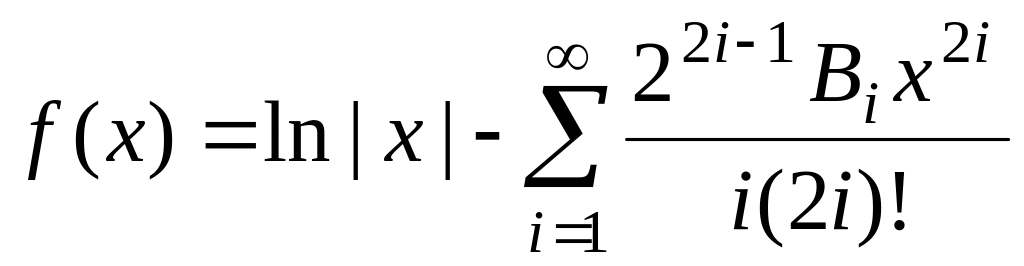 ,
де Ві
–
числа Бернуллі, fточ(х)=ln|sin(x)|.
,
де Ві
–
числа Бернуллі, fточ(х)=ln|sin(x)|.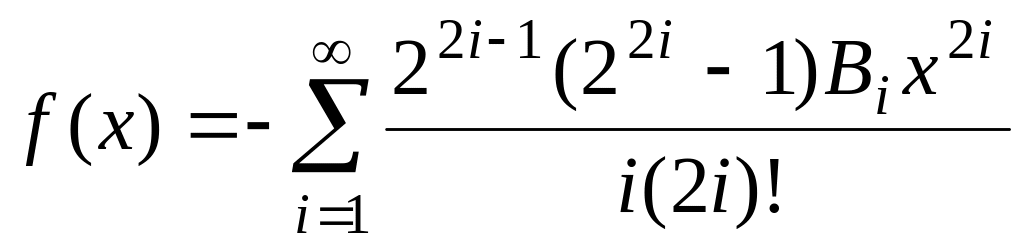 ,
де Ві
–
числа Бернуллі, fточ(х)=lncos(x).
,
де Ві
–
числа Бернуллі, fточ(х)=lncos(x).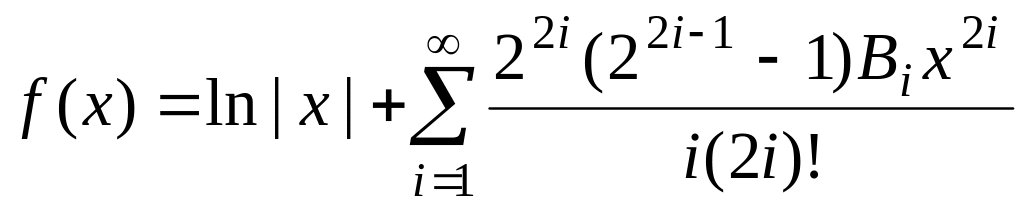 ,
де Ві–числа
Бернуллі, fточ(х)=ln|tg(x)|.
,
де Ві–числа
Бернуллі, fточ(х)=ln|tg(x)|.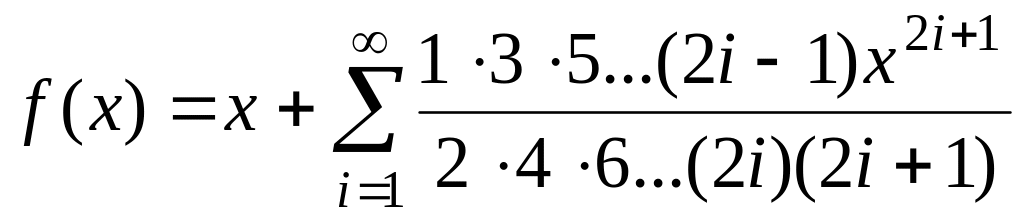 ,
fточ(х)=arcsin(x).
,
fточ(х)=arcsin(x). ,
fточ(х)=arccos(x).
,
fточ(х)=arccos(x).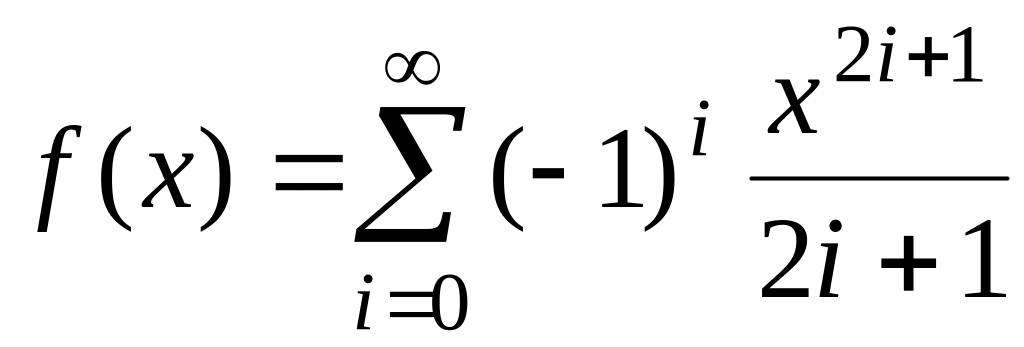 ,
fточ(х)=arctg(x).
,
fточ(х)=arctg(x).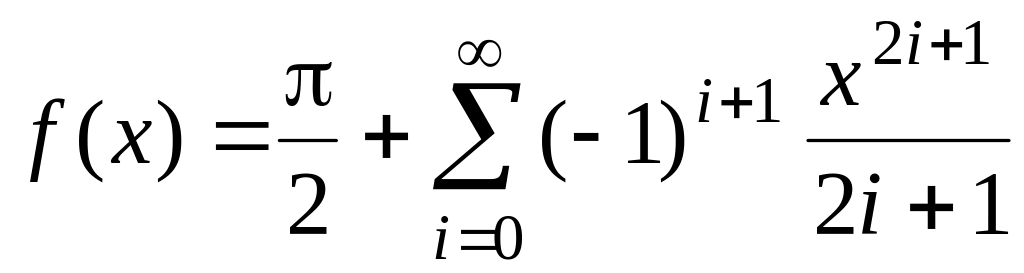 ,
fточ(х)=arcctg(x).
,
fточ(х)=arcctg(x).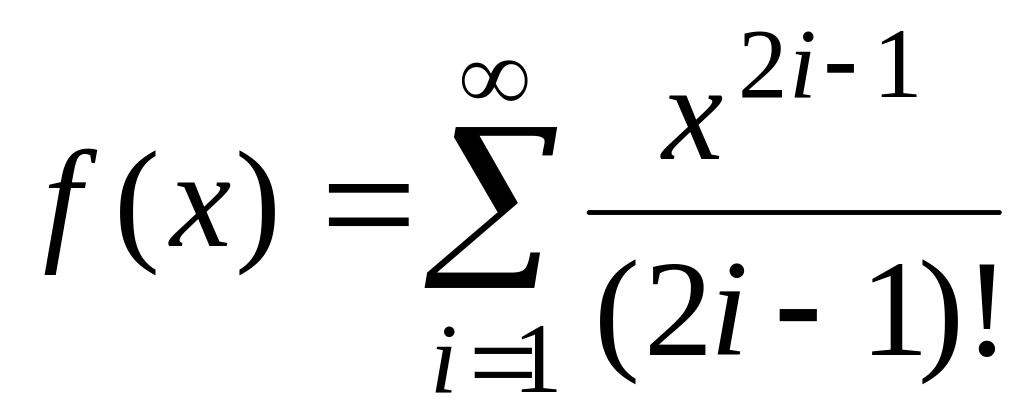 ,
fточ(х)=sh(x).
,
fточ(х)=sh(x).
Таблиця 1.1
Перші числа Бернуллі
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
Bk |
|
|
|
|
|
|
|
|
|
|
|
Таблиця 1.2
Перші числа Ейлера
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Еk |
1 |
5 |
61 |
1385 |
50521 |
2 702 765 |
199 360 981 |
Лабораторна робота № 2
ПРЯМІ МЕТОДИ РОЗВ'ЯЗУВАННЯ СИСТЕМИ
ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ
Для виконання роботи необхiдно записати систему рiвнянь у матричнiй формi i скласти програму її розв'язування одним з таких методiв:
1) Гаусса з порядковою реалiзацiєю; 2) Гаусса з вибором головного елемента по стовпцю. Порiвняти результати з простим методом Гаусса; 3) Гаусса з вибором головного елемента по всьому полю; 4) Жордана; 5) Жордана з вибором головного елемента. Порiвняти результати з простим методом Жордана; 6) оптимального виключення; 7) оптимального виключення з вибором головного елемента. Порiвняти результати з простим методом оптимального виключення; 8) LU - перетворення; 9) Гаусса з вибором головного елемента по стовпцю i без перестановки рядків; 10) Гаусса з порядковою реалiзацiєю i вибором головного елемента; 11) Гаусса з порядковою реалiзацiєю, вибором головного елемента i без перестановки рядків; 12) LU -перетворення по рядкам; 13) Жордана з вибором головного елемента i без перестановки рядків; 14) Гаусса з вибором головного елемента по всьому полю i без перестановки рядків та стовпцiв; 15) прогонки для довільної системи 1010.
Вивести вектор розв'язку та нев'язки. Вектор нев'язки обчислюють за початковою системою. Варiанти iндивiдуальних завдань наведенi в табл.1.3, варiанти систем рiвнянь, що розв'язуються - в табл.1.4. В цій таблиці перший стовпець - номер варіанту, наступні шістнадцять - елементи матриці А розміром 4x4, перелічені по стовпцям. Останні чотири стовпця таблиці 1.4 - елементи вектору В правої частини СЛАР.
Таблиця 1.3
Варіант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
Метод |
5 |
6 |
7 |
8 |
9 |
10 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Варіант |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
Метод |
10 |
11 |
12 |
13 |
14 |
15 |
8 |
9 |
10 |
11 |
Таблиця 1.4
№ |
1-й Стовпець |
2-й стовпець |
3-й стовпець |
4-й стовпець |
Права частина |
|||||||||||||||
1 |
4 |
3 |
100 |
2 |
1000 |
-1 |
-3 |
2 |
2 |
1 |
-2 |
0 |
3 |
-3 |
0 |
-1 |
5 |
-1 |
-3 |
-1 |
2 |
2 |
9 |
35 |
-8 |
1 |
100 |
-23 |
5 |
-1 |
3 |
3 |
2 |
2 |
2 |
95 |
4 |
9 |
5 |
6 |
3 |
3 |
5 |
10 |
-3 |
-3 |
0 |
9 |
4 |
-8 |
2 |
8 |
90 |
3 |
4 |
8 |
1 |
-5 |
8 |
0 |
4 |
6 |
4 |
-2 |
-7 |
-11 |
1000 |
0 |
0 |
10 |
8 |
9 |
7 |
1 |
0 |
65 |
2 |
0 |
7 |
7 |
4 |
4 |
8 |
5 |
3 |
10 |
8 |
5 |
0 |
1 |
4 |
2 |
67 |
12 |
5 |
98 |
7 |
3 |
1 |
80 |
6 |
3 |
3 |
9 |
6 |
8 |
-3 |
100 |
12 |
1000 |
8 |
6 |
6 |
-1 |
87 |
8 |
1 |
7 |
5 |
0 |
67 |
65 |
3 |
-5 |
0 |
7 |
-6 |
1 |
7 |
100 |
5 |
3 |
7 |
8 |
100 |
3 |
2 |
7 |
2 |
7 |
7 |
7 |
54 |
-6 |
7 |
-3 |
8 |
1 |
10 |
-2 |
2 |
1000 |
4 |
8 |
4 |
0 |
4 |
-5 |
6 |
8 |
5 |
0 |
5 |
3 |
2 |
2 |
3 |
9 |
0 |
-3 |
100 |
-3 |
-3 |
-2 |
9 |
3 |
0 |
54 |
34 |
4 |
100 |
4 |
-5 |
2 |
2 |
-4 |
9 |
3 |
10 |
0 |
23 |
9 |
1000 |
98 |
-3 |
-1 |
-5 |
34 |
100 |
-5 |
2 |
1 |
1 |
0 |
1 |
1 |
2 |
9 |
7 |
11 |
1 |
2 |
100 |
1000 |
5 |
0 |
8 |
9 |
100 |
-7 |
0 |
9 |
90 |
8 |
5 |
10 |
23 |
49 |
-3 |
5 |
12 |
8 |
10 |
14 |
1 |
1000 |
0 |
2 |
5 |
-1 |
500 |
29 |
13 |
900 |
5 |
6 |
47 |
1 |
2 |
34 |
6 |
13 |
-5 |
34 |
100 |
1000 |
9 |
0 |
67 |
9 |
35 |
400 |
78 |
4 |
700 |
1 |
8 |
5 |
7 |
4 |
8 |
3 |
14 |
67 |
78 |
4 |
7000 |
7 |
5 |
7 |
4 |
3 |
9 |
5 |
-3 |
-59 |
4 |
45 |
3 |
5 |
21 |
5 |
6 |
15 |
45 |
2 |
7 |
6000 |
5 |
0 |
56 |
3 |
7 |
4 |
7 |
4 |
7 |
4 |
-5 |
6 |
3 |
6 |
2 |
1 |
16 |
4 |
5 |
2 |
8 |
7000 |
0 |
89 |
7 |
0 |
0 |
8 |
6 |
5 |
9 |
1 |
2 |
5 |
32 |
-5 |
0 |
17 |
0 |
1 |
2 |
3 |
700 |
0 |
4 |
9 |
6 |
9 |
5 |
6 |
23 |
4 |
6 |
4 |
0 |
7 |
5 |
7 |
18 |
6 |
3 |
5 |
3 |
8 |
0 |
9 |
7 |
7 |
900 |
8 |
6 |
54 |
9 |
5 |
-1 |
3 |
0 |
7 |
5 |
19 |
7 |
8 |
5 |
700 |
4000 |
0 |
7 |
65 |
1 |
3 |
3 |
6 |
4 |
7 |
6 |
7 |
4 |
2 |
3 |
1 |
20 |
45 |
3 |
6 |
800 |
7 |
0 |
5 |
8 |
7 |
5 |
4 |
98 |
6 |
4 |
4 |
9 |
4 |
3 |
2 |
1 |
21 |
4 |
7 |
8 |
6 |
3000 |
0 |
8 |
-4 |
4 |
8 |
5 |
3 |
9 |
7 |
5 |
8 |
0 |
87 |
7 |
6 |
22 |
1 |
4 |
6 |
4 |
7000 |
0 |
5 |
9 |
0 |
7 |
6 |
5 |
4 |
3 |
7 |
8 |
8 |
0 |
7 |
6 |
23 |
2 |
4 |
7 |
5 |
9000 |
0 |
8 |
6 |
9 |
4 |
6 |
34 |
7 |
4 |
9 |
3 |
4 |
33 |
8 |
8 |
24 |
7 |
8 |
45 |
8 |
5000 |
0 |
8 |
5 |
4 |
3 |
7 |
8 |
7 |
3 |
2 |
3 |
1 |
4 |
6 |
7 |
25 |
0 |
8 |
6 |
0 |
4000 |
0 |
5 |
4 |
8 |
6 |
9 |
6 |
4 |
4 |
9 |
7 |
6 |
4 |
3 |
1 |
Лабораторна робота №3 ітераційні методи розв'язування систем
ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ
Записати систему рiвнянь, яку треба розв'язати, у матричнiй формi. Скласти програму для розв'язування системи iтерацiйним методом при = 0,001. У програмi використати один iз таких iтерацiйних методiв:
1) послiдовних наближень; 2) простої iтерацiї; 3) Зейделя; 4) Некрасова;
Як початкове наближення брати нульовий вектор. Передбачити максимально допустиму кількість iтерацiй, що дорiвнює 40. На кожнiй iтерацiї надрукувати її номер i вектор невiдомих.
На практицi звичайно вiдомi характеристики розв'язуваної СЛАР та умови збiжностi виконуються для застосованного методу. У цiй роботi такі умови можуть не виконуватися. Але оскільки вони є тiльки достатнiми, то спочатку треба спробувати розв'язати систему без її змiни. Якщо програма правильна (це можна визначити за допомогою тестової системи), але процес розбігається, то треба перетворити систему. Це можна зробити вручну, переставляючи рiвняння та обчислюючи їх лiнiйнi комбiнацiї, або за допомогою ЕОМ. Наприклад, можна використати процедуру Жордано з коефiцiєнтом R = R 1.1.
Надрукувати початкову та перетворену системи. Для обчислення вектора нев'язок використовувати початкову систему. Данi, якi виводяться на кожнiй iтерацiї, друкувати в одному рядку.
У програмi
передбачити побудову одного з наступних
графiкiв (k
- кiлькiсть виконаних iтерацiй;
- припустима похибка,
![]() x*-
точний розв'язок системи):
x*-
точний розв'язок системи):
1. Залежнiсть k() для = 10-1, 10-2, 10-3, 10-4, 10-5.
2. Залежнiсть кількості необхiдних iтерацiй вiд початкового значення для першої компоненти вектора невiдомих x, яка набирає значення 0,1,2,...,10.
3. Залежнiсть величини = ||x(n) - x(n-1)|| від n для n=1,2,...,k при = 0,001.
4.Залежнiсть
величини
![]() від n
для n=1,2,...,k
при =0,001.
від n
для n=1,2,...,k
при =0,001.
5. Залежнiсть величини || x(n)- x*|| від n для n=1, 2,...,k при =10-6.
6.
Залежнiсть величини
![]() вiд n
для n
=1, 2,..., k
при =10-7.
вiд n
для n
=1, 2,..., k
при =10-7.
7. Залежності k(), = 10-1, 10-2, 10-3, 10-4, 10-5 для свого методу та методу Зейделя для однiєї й тiєї самої системи рiвнянь на одному полi.
8. Те саме, що у п.7, але порiвняти свiй метод з методом Некрасова.
Варiанти iндивiдуальних завдань наведенi у табл.1.5.
Таблиця 1.5
Варіант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Метод |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
Графік |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Варіант |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
Метод |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
1 |
Графік |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1 |
Лабораторна робота №4
