
- •Министерство образования рф
- •1. Матрицы и основные операции над ними
- •1.1. Понятие матрицы
- •1.2. Виды матриц
- •1.4. Действия над матрицами
- •1.5. Миноры и алгебраические дополнения
- •1.6. Присоединенная и обратная матрицы
- •1.7. Ранг матрицы и элементарные преобразования матрицы
- •1.8. Вырожденность (дефект) матрицы
- •2. Векторы и основные операции над ними
- •2.1. Понятие вектора
- •2.2. Основные операции над векторами
- •3. Линейное векторное метрическое нормированное пространство
- •3.1. Понятия и определения
- •3.2. Линейное преобразование
- •3.3. Подпространство
- •4. Матричные преобразования
- •4.1. Преобразование подобия
- •4.3. Конгруэнтное преобразование
- •5. Собственные числа, собственные векторы и диагонализация матриц
- •5.1. Собственные числа и собственные векторы матрицы
- •5.2. Диагонализация матриц.
- •6. Функции от матриц
- •6.1. Степени матриц
- •6.2. Функции от матриц
- •6.3. Теоремы о функциях от матриц
- •7. Квадратичная форма
- •Список литературы
6. Функции от матриц
6.1. Степени матриц
Произведение матриц AAA…A, где A – квадратная матрица порядка n, можно записать в виде Ak, где k означает число сомножителей, входящих в произведение. Это произведение называется k-й степенью матрицы A. Оно обладает свойствами
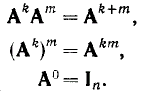
Те же правила справедливы при возведении матрицы в отрицательную степень при условии, что матрица неособенная, то есть существует обратная матрица. Имеем
![]()
Подобные правила применяются и в случае вычисления дробной степени матрицы. Так, если Am=B, то A является корнем m-й степени B. Не существует общего правила определения, каким количеством корней степени m обладает матрица B, – число корней зависит от вида матрицы.
6.2. Функции от матриц
Матричный многочлен – это выражение вида
![]()
Разложение на множители этого многочлена, или факторизация матричного многчлена, имеет вид
![]()
Бесконечный ряд матриц:
![]()
Геометрический ряд:
![]()
Экспоненциальная функция
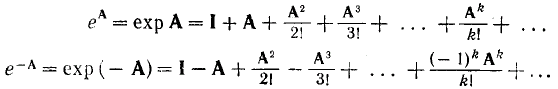
Можно показать, что этот ряд сходится равномерно и абсолютно. Произведение матричных экспонент:
eAeB=eA+B
Синусоидальная функция:
![]()
Косинусоидальная функция:
![]()
, где комплексная экспонента определяется как
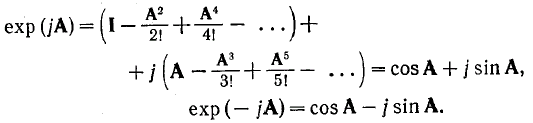
Гиперболический синус
![]()
Гиперболический косинус
![]()
6.3. Теоремы о функциях от матриц
Теорема Кэли-Гамильтона: матрица A удовлетворяет собственному характеристическому уравнению. Этот результат можно записать в виде:
![]()
На основе этой теоремы можно представить многочлен n-го порядка от матрицы A в виде линейной комбинации I, A, A2, …, An-1 или многочлена n-й степени относительно A.
Теорема Сильвестра: если N(A) – матричный многочлен от A и если квадратная матрица A содержит n различных характеристических чисел, то многочлен от A можно записать в виде
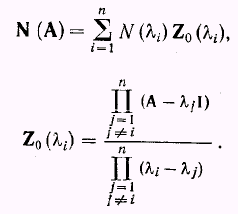
Можно показать, что
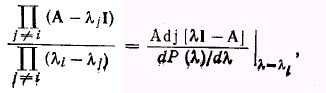
где P() – характеристический многочлен A, а потому теорема Сильвестра может быть записана в виде
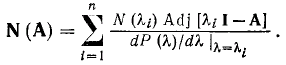
Если матрица A содержит кратные характеристические корни, то необходимо использовать так называемую вырожденную форму теоремы Сильвестра. Пусть характеристический корень имеет порядок s. Тогда член суммы, соответствующий кратному корню i, можно представить в виде
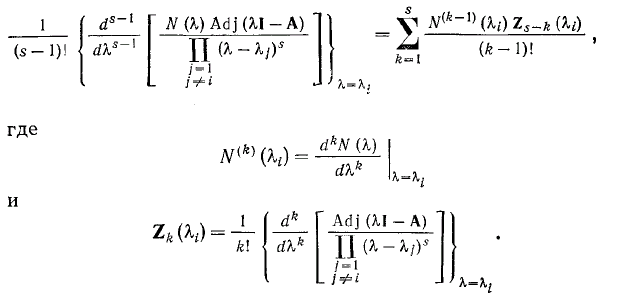
7. Квадратичная форма
Квадратичной формой называется выражение:
![]()
Этой квадратичной форме соответствует матрица
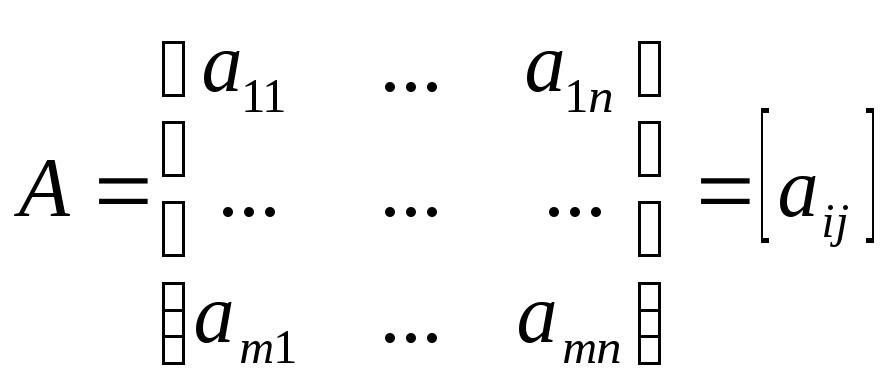
Сделаем следующее преобразование с каждым членом квадратичной формы:
a12x1x2+a21x2x1=x1x2(a12+a21)=0.5(a12+a11)x1x2+0.5(a12+a11)x1x2
Как видно, матрица, соответствующая этой квадратичной форме, является симметрической. Квадратичную форму можно представить в матричном виде:
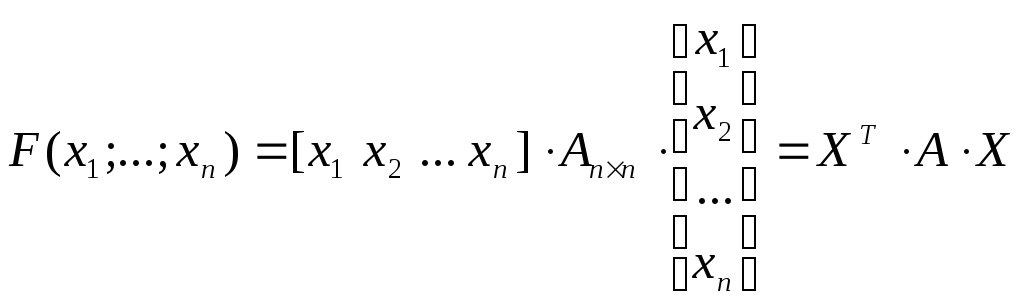
Квадратичная форма имеет канонический вид, если она содержит только квадраты переменных, то есть
![]()
Ей соответствует диагональная матрица A=diag(I). Следовательно, чтобы привести квадратичную форму к каноническому виду, нужно выполнить над ней такое преобразование, которое приведет матрицу, соответствующую ей, к каноническому виду, например, диагонализацию матрицы.
Если над квадратичной формой сделано некоторое линейное преобразование, то первоначальная и полученная квадратичные формы называются конгруэнтными.
Пусть над квадратичной формой сделано преобразование вида:
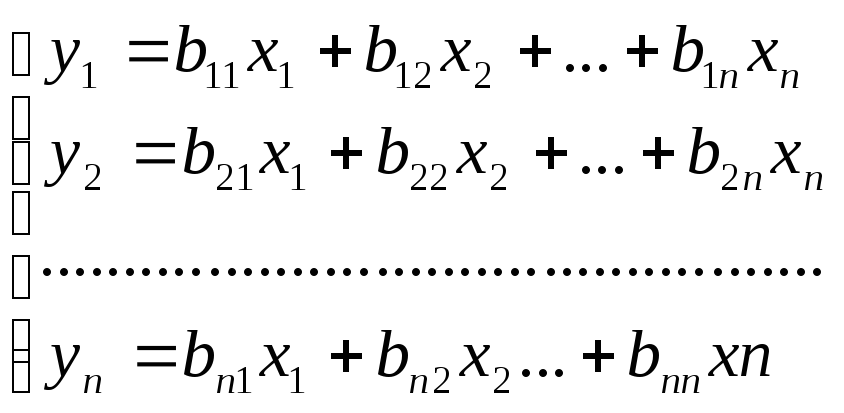
или короче Y=BX, где B=[bij]. Тогда квадратичная форма после преобразования принимает вид
F(Y)=YTAY
F(X)=(BX)TABX=XTBTABX=XTCX, где C=BTAB.
Квадратичная форма в независимости от выбора базиса в каноническом виде имеет одинаковое количество положительных и отрицательных коэффициентов.
Квадратичная форма называется положительно определенной, если для любого xR
F(X, X)>0
и отрицательно определенной, если для любого xR
F(X, X)<0.
В случае нестрогого неравенства квадратичная форма называется положительно полуопределенной и отрицательно полуопределенной соответственно.
Чтобы определить положительность квадратичной формы, служит критерий Сильвестра: квадратичная форма является положительно определенной тогда и только тогда, когда все угловые миноры матрицы, соответствующей этой квадратичной форме, положительны. Квадратичная форма является отрицательно определенной тогда и только тогда, когда угловые миноры матрицы, соответствующей этой квадратичной форме, будут чередоваться по знакам, начиная с отрицательного.
