4.3. Конгруэнтное преобразование

Две матрицы называются конгруэнтными, если существует неособенная матрица Q, удовлетворяющая равенству

B=QTAQ.

5. Собственные числа, собственные векторы и диагонализация матриц

5.1. Собственные числа и собственные векторы матрицы

Предположим, что среди бесконечного множества одномерных пространств R1 найдутся такие, которые будут инвариантны относительно преобразования y=Ax, то есть для любого xR1. Обозначим через  отношение y к x, которое при этом будет просто вещественным числом, то есть можно записать y=x. Таким образом, если R1 – инвариантное подпространство, то для xR1 имеет место равенство

Ax=x.

Вектор x0, удовлетворяющий этому соотношению, называют собственным вектором матрицы A, а число  – собственным значением матрицы A.

Для определения характеристических чисел матрицы перепишем это соотношение в ином виде, введя тождественное преобразование x=Ix. При этом получаем

(A–I)x=0

Это соотношение представляет собой систему линейных однородных уравнений. Чтобы эта система имела нетрививльное решение, необходимо и достаточно, чтобы det (A–I)=0. При этом сами переменные, то есть вектор x, определяются с точностью до постоянного множителя. Соотношение det (A–I)=0 называют характеристическим уравнением матрицы A, представляющим собой алгебраическое уравнение n-й степени относительно . Это уравнение имеет n корней, среди которых могут быть и одинаковые, являющиеся собственными значениями матрицы A.

Подставив любое собственное значение i в исходную систему уравнений, получим уравнение

(A–iI)x=0,

которое имеет нетривиальное решение. Это решение дает вектор xi, определяемый с точностью до скалярного множителя. Этот вектор и называется характеристическим вектором матрицы A.

5.2. Диагонализация матриц.

Для матрицы A, имеющей n различных характеристических чисел, преобразование вида M-1AM приводит к диагональной матрице D, где M называется модальной матрицей. Матрица M составлена из характеристических векторов матрицы A.

Однако матрица общего вида размерности (nn) с кратными характеристическими числами может содержать меньше, чем n линейно независимых характеристических векторов; поэтому приведение к диагональной форме посредством преобразования может оказаться невозможным. Однако можно показать, что произвольная квадратная матрица путем преобразования подобия приводится к канонической матрице Жордана, обладающей следующими свойствами:

1. Диагональные элементы этой матрицы являются характеристическими числами A.

2. Все элементы, лежащие ниже главной диагонали, равны нулю.

3. Если соседние элементы на главной диагонали одинаковы, то элементы, непосредственно находящиеся справа от главной диагонали, равны единицы. Типичная жорданова форма имеет вид:

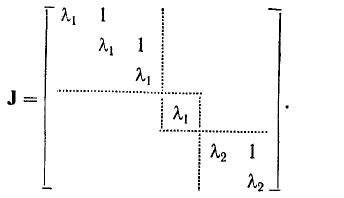
Заметим, что единицы встречаются в блоках вида

Они называются клетками Жордана.

Количество клеток Жордана, связанных с данным характеристическим числом i, в соответствии с преобразованием подобия, приводящим к жардановой форме, равное количеству собственных векторов, связанных с характеристическим числом, то есть q-дефекту [iI–A]. Однако, определить порядки клеток Жордана нелегко. Поэтому неясно, получается ли в результате преобразования J=M-1AM приведенная выше жорданова форма или форма

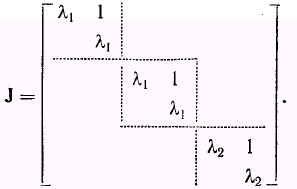
Полезно знать, что в случае полной вырожденности не будет присутствовать ни одной единицы. В случае простой вырожденности (q=1) все элементы, непосредственно лежащие справа от главной диагонали, равны единице. Для случаев, не укладывающихся в упомянутые, необходимо использовать для определения J и M метод проб и ошибок, основанный на равенстве

AM=MJ.

Пусть столбцы M обозначаются x1, x2, …, xn. Тогда существует клетка Жордана порядка m, связанная с I лишь в том случае, если m линейно-независимых векторов x1, x2, …, xm удовлетворяют уравнениям:

Эти выражения применимы для каждой клетки Жордана.