2. Следование, эквивалентность и преобразование формул

Введем на множестве M отношения следования и эквивалентности.

Формула B следует из формулы A (обозначается AB), если она истинна на всех наборах высказывательных переменных, на которых истинна формула A.

Теорема 2.1. Формула B следует из формулы A тогда и только тогда, когда тождественно истинна формула AB.

Доказательство. Пусть формула B следует из формулы A. Импликация AB ложна только на тех интерпретациях, на которых формула А истинна, а В ложна, что невозможно в силу условия.

Покажем обратное. Пусть AB – тождественно истинна, тогда если на некоторой интерпретации формула А истинна, то и формула В истинна на ней, что и означает AB.

Формула A эквивалентна формуле B (обозначается A  B), если они следуют друг из друга, то есть AB и BA. Легко показать, что это определение эквивалентно определению, введенному в п.1.

Теорема 2.2. Формула A эквивалентна формуле B тогда и только тогда, когда тождественно истинна формула A~B.

Доказательство аналогично доказательству теоремы 2.1.

Приведем список основных тавтологий, выражающих свойства логических операций.

1. Коммутативность:

X Y  Y X, X Y  YX.

2. Ассоциативность:

(X Y)Z  X (YZ), (XY)Z  X(YZ).

3. Идемпотентность:

XX  X, XX  X.

4. Законы поглощения:

X(XY)  X, X(XY)  X.

5. Взаимная дистрибутивность конъюнкции и дизъюнкции:

X (YZ)  (X Y)(X Z), X (YZ)  (XY)(XZ).

6. Свойства констант:

X0  Л, X1  X,

X0  X, X1  1.

7. Законы де Моргана:

, .

8. Инволютивность:

.

9. Закон противоречия:

0.

10. Закон исключенного третьего:

1.

Эквивалентность большинства из этих формул непосредственно следует из определения операций или проверяется построением таблиц истинности.

Пусть U – некоторая формула, в которую входит переменная X или подформула А, что обозначается U(, X,) или U(,А,). Пусть В – некоторая формула. Запись U(¼, X,¼){В//X} обозначает формулу, полученную из формулы U подстановкой формулы В вместо всех вхождений переменной X, а U(¼, А,¼){В/А} – формулу, полученную из формулы U подстановкой формулы В вместо некоторых (в частности, вместо одного) вхождений подформулы А.

Теорема 2.3 (правило подстановки). Если U(, X,) – тавтология и В – любая формула, то U(¼, X,¼){В//X} – тавтология.

Теорема 2.4 (правило замены). Если A есть некоторая подформула формулы U и A эквивалентна формуле B, то формула, полученная заменой A в формуле U на B, эквивалентна U. Иными словами, если U(¼, А,¼) и A  B, то U  V= U(¼, А,¼){В/А}.

Например, так как AB  , то (AB)C  ()C.

Следствие. Если U~A и V~B, то:

1) UV AB;

2) UV AB;

3) UV AB;

4) (U~V)  (A~B);

5) U  A.

Теоремы 2.3, 2.4 и ее следствие позволяют преобразовывать формулы, упрощая их, и доказывать эквивалентность формул.

Примеры.

1. Докажем 1-й из законов поглощения X(XY)  X.

.

При доказательстве использовано правило замены.

2. Упростить формулу .

Так как  X в силу подстановки в закон поглощения, тогда, используя правило замены получим

.

Приведем еще несколько эквивалентностей, имеющих широкое применение.

11. .

12. .

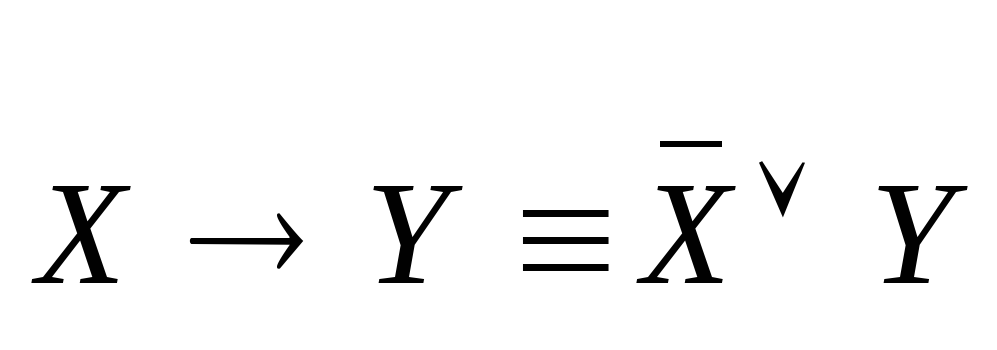13. Законы склеивания

, .

Эквивалентность формул является отношением эквивалентности, поэтому множество M можно разбить на классы эквивалентности, включив в один класс эквивалентные между собой формулы. Каждой формуле U соответствует класс эквивалентности, который обозначается [U].

Определение. Формула называется приведенной, если она содержит операции конъюнкции, дизъюнкции и операцию отрицания, относящуюся к высказывательным переменным.

Теорема 2.5. Каждый класс эквивалентности [U] может быть представлен приведенной формулой, т.е. для любой формулы UM существует приведенная формула V.

Доказательство теоремы проведём конструктивно, то есть определим порядок построения приведенной формулы.

1. Удаляются операции импликация и эквиваленция по формулам 11, 12.

2. Операции отрицания спускаются до высказывательных переменных с помощью законов де Моргана и двойного отрицания.

3. Если это возможно, то полученная приведенная формула упрощается с помощью свойств 3, 4, 5, 6, 9, 10.

Таким образом, проверить эквивалентность формул, тождественную истинность и ложность формулы или упростить ее можно с помощью этого алгоритма.

Приведенная формула для данного класса эквивалентности не является единственной.

Задание. Упростить формулу .

Решение. 

 A.

Определение. Формула U^d называется двойственной к приведенной формуле U, если она получена заменой операций конъюнкции на дизъюнкции и наоборот.

Теорема 2.6 (принцип двойственности). Пусть U() – приведенная формула, тогда

U^d() = U().

Доказательство. Число логических операций в формуле U называется рангом формулы и обозначается r(U). Проведем доказательство индукцией по k = r(U).

1⁰. k = 0. В этом случае U = X_i , следовательно, U^d = X_i    U ().

2 ⁰. Предположим, что теорема верна при k  m.

3 ⁰. Покажем, что она верна при k = m + 1.

Пусть U₁ и U₂ – подформулы U. Каждая из них образована посредством не более, чем m операций, и следовательно, для них теорема верна.

Возможны следующие случаи

а) U =  U₁;

б) U = U₁  U₂;

в) U = U₁  U₂.

Случай а) эквивалентен условию 1⁰ и при нем теорема верна. В случаях б) и в) заменим в каждой из U_i конъюнкцию на дизъюнкцию и наоборот. По определению двойственности будем иметь, соответственно, б): U^d = U U и в): U^d = U  U.

В силу законов де Моргана и предположения индукции будем иметь в случае б):

U^d = U U = (U₁ ())  (U₂ ()) 

  (U₁ ()  U₂ ()) =  U().

В случае в) выкладки аналогичны. Теорема доказана.

Следствие. Если U – ТИ-формула, то U^d – ТЛ-формула.

Теорема 2.7. Если U  V, то U^d  V^d.

Доказательство. Если U  V, то (U)  (V). Значит, в силу теоремы 2.6, U^d(Х₁, …, Х_n) = U() и V^d(Х₁, …, Х_n) = V().

Отсюда: U^d = (U())  (V()) = V^d. В силу транзитивности эквиваленции, получим U^d  V^d , что и требовалось доказать.