
Данилов. Определение внутренних усилий
.pdfМинистерство образования и науки Российской Федерации
ГОУ ВПО «Алтайский государственный технический университет им. И.И. Ползунова»
А.В.Данилов, Н.В. Котенева
ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ
Методическая разработка и варианты заданий для студентов строительных специальностей
Барнаул 2002
УДК 620.17(0.75.5)
Данилов А.В., Котенева Н.В. Определение внутренних усилий: Методическая разработка и варианты заданий для студентов строительных специальностей/ АлтГТУ им. И.И.Ползунова. – Барнаул: Изд-во АлтГТУ, 2002. – 43с.
В данной работе вводится понятие внутренних усилий и их определение методом сечений. Разобраны примеры построения эпюр внутренних усилий с использованием дифференциальных зависимостей между Qy, Mx, q. Рассмотрены примеры графического интегрирования нагрузки, помогающие студентам контролировать правильность построения эпюр внутренних усилий.
Предлагаемые варианты домашних заданий охватывают линейные, плоские и пространственные расчетные схемы.
Рассмотрена и одобрена на заседании кафедры «Прикладная механика». Протокол № 8 от 02. 07. 02
2
Внутренние усилия, их определение.
Все твердые тела имеют определенные размеры и форму вследствие наличия сил сцепления между частицами вещества. Так расстояния между атомами вещества определяются силами взаимного притяжения и отталкивания, имеющими электрическую основу.
Под внешним воздействием твердые тела деформируются, т.е. меняют свои размеры и форму. Под действием деформаций меняются расстояния между частицами вещества, что приводит к изменению сил взаимодействия между ними. Усилия, вызванные механическим изменением расстояния между частицами вещества, называются внутренними усилиями.
Основным методом определения внутренних усилий является метод сечений, который базируется на аксиоме статики об отбрасывании связей. Согласно этой аксиоме, например, при определении опорных реакций, взамен отброшенных внешних связей прикладываются реакции этих связей. Затем, рассматривая равновесие тела под действием заданных сил и приложенных реакций, определяют величину и истинное направление реакций связей.
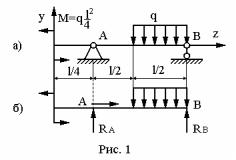
Пример 1.
В отличие от внешних сил, направления реакций неизвестно, поэтому нужно задаться их направлением. Это существенно для составления уравнений равновесия и определения истинных направлений реакций. Введя систему координат, YOZ будем считать положитель-
ным направлением RA и RB вдоль положительного направления
OY . Отметим, что HA 0 в силу отсутствия горизонтальных про-
3
екций внешних нагрузок. Для схемы Рис. 1б составим уравнения сумм моментов относительно оси OX в точках A и B
mXA M RB q |
|
|
3 |
0 |
|
RB |
q |
||
2 |
4 |
8 |
|||||||
|
|
|
|
|
|
|
3 |
|
|
mXB RA M q |
|
|
|
0 |
|
RA |
|
q |
|
2 |
4 |
8 |
|||||||
Знак «плюс» полученный для RA, RB означает, что их дейст-
вительное направление будет совпадать с принятым.
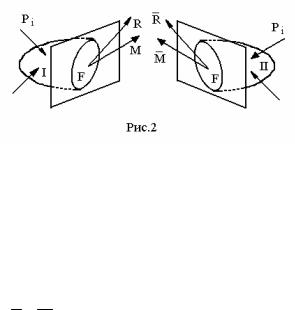
Применяя ту же аксиому для определения реакций внутренних связей (внутренних усилий), необходимо разрушить все внутренние связи по некоторой внутренней поверхности тела. Осуществить это можно мысленным рассечением тела плоскостью на две части.
Причем каждая часть будет ограничена плоской фигурой F (рис. 2), получающейся в результате пересечения секущей плоскости и боковой поверхности тела. В соответствии с принятой гипотезой об однородности и сплошности тела, в каждой точке этой плоской фигуры нужно полагать наличие сил внутреннего взаимодействия между частицами вещества. Если просуммировать эти силы по поверхности F , то в соответствии с основной теоремой статики, их можно привести в одну точку в виде главного вектора R и главного момента M .
Главный вектор R и главный момент M , действующие на первую часть тела (рис. 2), есть действие второй части тела на первую. В
свою очередь R, M - действие первой части тела на вторую. Очевид-
но, по третьему закону механики, |
|
R |
|
|
R |
, |
|
M |
|
|
M |
. Таким обра- |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4
зом, можно говорить о внутреннем усилии как о действии одной части тела на другую по плоскости их разделения.
Если твердое тело под действием внешних сил Pi находилось в
равновесии, то и часть тела под действием сил P , действующих по поверхности этой части, и R и M , действующих по поверхности F , должна находиться в равновесии в силу определения R и M . Из рас-
смотрения равновесия любой части тела внутренние усилия R, M
могут быть выражены через внешние воздействия Pi .
Для практического решения этой задачи:
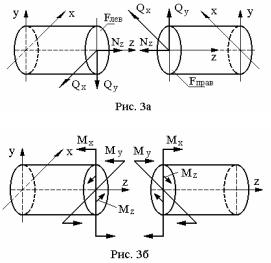
1)Введем систему прямоугольных координат. Рассматривая тела в виде стержней, условимся, одну из координатных осей совмещать с осью стержня, а две другие с плоскостью параллельной F. Так как, в результате рассечения тела на две части, получаются две поверхности F , то будем их различать на левую, для которой ось координат открыта (внешняя нормаль) и правую, для которой нормальная ось входит внутрь объема тела (внутренняя нормаль) (рис. 3а).
2) В сопротивлении материалов компоненты главного вектора
R NzQxQy (рис. 3а) и главного момента M Mz,Mx,M y (ри-
сунок 3б) имеют свои названия и обозначения.
5

Nz- продольная сила, т.к. она направлена по оси стержня. Ее положительное направление в левом и правом сеченияx - от сечения
Qx, Qy- поперечные (перерезывающие) силы, так как они на-
правлены поперек оси стержня. Их положительные направления: в левом сечении против осей координат, в правом - по осям координат.
M z - крутящий момент, он действует вокруг оси стержня, т.е. в
плоскости XOY . Его положительное направление устанавливается как направление против часовой стрелки, если смотреть на сечение (левое или правое).
Mx,M y- изгибающие моменты, действуют соответственно в
плоскостях YOZ и XOZ, искривляют ось OZ . Их направления счи-
таем положительными, если ось OZ искривляется с положительной кривизной. Напомним, что положительная кривизна имеет направление выпуклости в сторону отрицательного направления координатной оси (рис. 4).
Примечание: В сопротивлении материалов положительные направления внутренних усилий служат не только для установления их действительных направлений, но и для определения типа деформации. Поэтому их не следует задавать произвольно.
3) В различных сечениях стержня внутренние усилия могут принимать различные значения и меняться по различным законам по длине стержня: Введя понятие силового участка как интервала стержня, на котором внутреннее усилие меняется по одному закону, необходимо установить его границы в выбранной системе координат.
Границами таких участков считают начало или конец стержня, точку приложения сосредоточенной нагрузки (P или m), начало или конец распределенной нагрузки.
6

Совмещая начало координат с левым концом стержня в примере 1 (Рис. 16), получим границы силовых участков:
При Z 0 (начало стержня, точка приложения M);
Z /4 (точка приложения RA );
Z 34 (начало распределенной нагрузки);
Z 34 (начало распределенной нагрузки);
Z 5 (конец распределенной нагрузки, конец стержня).
4
Интервал стержня между границами, включая границы, является силовым участком. Таким образом, в данном примере будет три силовых участка:
I 0 Z |
|
; |
II |
|
Z |
3 |
; |
III |
3 |
Z |
5 |
. |
|
4 |
|
4 |
|
||||||||
4 |
|
|
4 |
|
|
4 |
|
|||||
4) Рассечем стержень (рисунок 1б) в промежутке 0 и отбро-
4
сим правую часть (Обычно отбрасывают ту часть, которая содержит неизвестные нагрузки или большее количество нагрузок). На левую часть (рис.5а) действует внешняя нагрузка M , а действие отброшенной части заменено внутренними усилиями, направленными в соответствии с пунктом 2.
Так как задача плоская (все нагрузки лежат в плоскости ZOY ) и отсутствуют горизонтальные проекции внешних нагрузок, из шести компонент внутренних усилий отличными от нуля будут только два (Qy, Mx), указанных на рис. 5а.
7

Рассматривая равновесие всех сил, действующих на эту часть, запишем уравнения сумм проекций на ось Y и сумму моментов относительно оси X , которая изображается точкой c.
Y Qy 0 |
|
Qy 0 |
а) |
|||
|
|
|
Mx M 0 |
|
||
|
|
c |
|
Mx M |
||
|
mx |
|
|
|
|
|
Результат показывает, что в промежутке 0 перерезывающее
4
усилие равно нулю, а изгибающий момент будет постоянным и направлен в обратном направлении.
Для определения внутренних усилий по всей длине стержня такие же действия повторяют на каждом силовом участке. Так на втором участке получаем (Рис.5б)
Y Qy RA 0; |
|
|
|
|
3 |
|
|
|
|
|
|
||
Qy 8q |
|
|
|
|
|
б) |
|||||||
|
|
|
|
z |
|
0 |
|
|
|
|
|
|
|
m |
|
Mx M R |
|
|
|
Mx |
3 |
|
|
q 2 |
|||
x c |
A |
4 |
8 |
q z |
4 |
|
. |
||||||
|
|
|
|
|
|
|
|
4 |
|||||
Результат показывает, что перерезывающее усилие в промежутке
3 будет постоянным, а изгибающий момент представляется ли-
4 4
нейной функцией от осевой координаты Z .
Рассекая стержень на третьем участке, видим, что проще рассматривать правую часть (Рис. 5в). Так как правое сечение имеет внутреннюю нормаль, то перерезывающее усилие направлено в сторону положительной оси ОY, а изгибающий момент искривляет стержень с положительной кривизной. Обратим внимание на то, что длина правой
части равна |
5 |
Z. |
|
|
|
|
|
|
|
|
|
|
|||
4 |
|
|
|
|
|
|
|
|
q |
||||||
|
|
|
5 |
|
|
|
|
5 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
Y Q |
y |
q |
|
z |
R |
0; Q |
y |
q |
|
z |
|
|
; |
||
|
4 |
|
|||||||||||||
|
|
|
4 |
|
B |
|
|
|
8 |
|
|||||
|
|
|
|
|
|
|
|
1 5 |
|
|
|
2 |
|
|
5 |
|
|
в) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
m |
x c |
M |
x |
q |
|
|
|
z |
|
R |
B |
|
|
z |
0 |
|
||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
2 4 |
|
|
|
|
|
|
4 |
|
|
|
|||||||
|
|
q |
|
5 |
|
|
2 |
|
q |
5 |
|
|
|
|
|
|
|
|||||
Mx |
|
|
|
|
z |
|
|
|
|
|
|
z . |
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
4 |
|
|
|
|
|
|
8 4 |
|
|
|
|
|
|
|
||||||
8
В промежутке |
3 |
|
5 |
перерезывающее усилие меняется по |
4 |
|
|||
|
4 |
|
||
линейному закону, а изгибающий момент по закону квадратной параболы.
Таким образом, для выявления закона изменения внутренних усилий в пределах силового участка необходимо:
Рассечь стержень на две части между границами силового участ-
ка.
Отбросить одну из частей, а именно ту которая содержит неизвестные внешние нагрузки, или содержит большее количество нагрузок
Заменить действие отброшенной части на оставшуюся внутренними усилиями, определив их направление в зависимости от рассматриваемого сечения (левого или правого)
Уравновесить действие внешних сил и внутренних усилий, действующих на рассматриваемую часть, т.е. записать уравнения равновесия для рассматриваемой части.
Кратко эти действия именуются аббревиатурой РОЗУ. Исследование величины и направления внутренних усилий про-
водят с помощью графического представления полученных функций на каждом участке. При этом используются обычные приемы геометрического исследования функций, известные из курса высшей математики и установленные в сопротивлении материалов дифференциальные зависимости между интенсивностью внешней распределенной нагрузки и внутренними усилиями:
|
dN |
dQy |
dMx,y |
d2Mx,y |
|
|
dMz |
|
||||
|
|
t; |
|
qy; |
|
Qyx; |
|
|
qy,x; |
|
|
m |
|
|
|
|
|
dz2 |
|
dz |
|||||
|
dz |
dz |
dz |
|
|
|
|
|||||
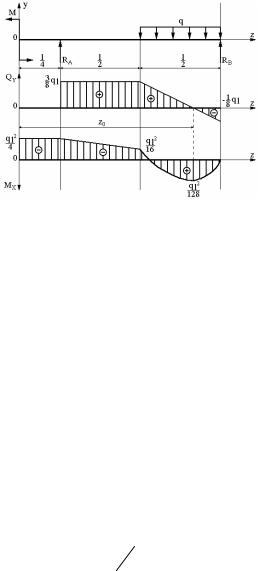
Рассмотрим построение графиков Qy |
и Mx , для примера 1. |
|||||||||||
Вычерчиваем в масштабе стержень с нагрузкой, а под ним две |
||||||||||||
системы координат для внутренних усилий |
Qy и Mx . |
Оси абсцисс |
||||||||||
графиков совпадают с осью координат 0Z, |
ось ординат Qy совпа- |
|||||||||||
дает с осью 0Y , |
ось ординат усилия Mx , |
направляется против оси |
||||||||||
0Y (рисунок 6). |
|
|
|
|
|
|
|
|
|
|
||
9
|
|
|
|
|
|
|
Рис. 6. |
|
|
|
|
|
|
|
|
|
|||
|
|
Из выражений а) |
на промежутке |
0 |
|
следует, чтоQy |
0, |
а |
|||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||
M |
|
Z |
|
|
M |
q |
, это означает, что обе функции изобража- |
||||||||||||
|
|
||||||||||||||||||
x |
4 |
||||||||||||||||||
|
|
4 |
|||||||||||||||||
|
Z 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ются прямой параллельной оси абсцисс. |
Однако расстояние прямой |
||||||||||||||||||
Qy |
|
от оси OZ равно нулю, а прямой Mx |
|
это расстояние равно |
q |
, |
|||||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||||
которое откладывается в условном масштабе. Проводим эти линии. |
|
||||||||||||||||||
|
|
Из выражений б) на промежутке |
|
|
3 |
. График Qy изобража- |
|||||||||||||
|
|
4 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
3 |
|
|
|
|||
ется прямой параллельной оси 0Z и проходящей выше 0Z на |
|
q . |
|||||||||||||||||
8 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
График Mx изображается прямой с угловым коэффициентом, прохо-
дящей на краях промежутка через ординаты:
|
Z 3 |
4 |
|
|
q 2 |
|
|
|
|||||
Mx |
|
|
16 |
|||
Z |
|
|
q |
2 |
||
|
4 |
|
|
|||
|
|
|
|
|
||
|
|
|
|
4 |
|
|
|
10 |
|
|
|
|
|
