
Данилов. Определение внутренних усилий
.pdf
Наконец, на промежутке |
3 |
|
5 |
из выражений в) следует, что |
4 |
|
|||
|
4 |
|
||
график Qy изображается прямой с угловым коэффициентом прохо-
дящей на краях промежутка через ординаты:
|
|
5 |
|
|
q |
; |
||
Qy |
|
|
|
|||||
4 |
|
|
8 |
|
||||
|
3 |
|
|
3 |
|
q |
||
|
4 |
|
8 |
|
|
|||
График Mx изображается квадратной параболой, которая долж-
на быть исследована на экстремум и на направление выпуклости-
вогнутости. Из дифференциальных зависимостей следует, что Qy яв-
ляется первой производной от Mx . Так как Qy на промежутке
3 5 принимает нулевое значение, меняя знак с плюса на минус
4 4
при возрастании Z , функция Mx имеет на этом промежутке экстре-
мум типа максимума. Определим положение экстремума, приравняв нулю выражение перерезывающей силы на данном участке.
|
5 |
|
|
|
q |
|
|
|
|
|
|
|
|
9 |
|
|||||
Qy |
q |
|
Z0 |
|
|
|
|
|
0 |
|
|
Z0 |
|
|
||||||
|
|
8 |
|
|
8 |
|||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Определим значение максимума, подставив |
Z0 |
в |
выражение |
|||||||||||||||||
Mx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max Mx |
q |
|
|
2 |
q |
|
q |
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
||||||
|
|
|
8 |
8 |
128 |
|
|
|||||||||||||
|
|
|
|
|
2 |
8 |
|
|
|
|
|
|
||||||||
Определяем направление выпуклости кривой (знак кривизны). Знак кривизны определяется знаком второй производной функции
Mx , которой является интенсивность распределенной нагрузки. Так как интенсивность qпротивоположна оси 0Y, она имеет отрицатель-
ный знак и график Mx имеет отрицательную кривизну. Следователь-
но, выпуклость графика направлена в сторону положительной оси
11
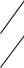
Mx . Вычислив значения Mx на краях промежутка, проводим кривую через три точки
Mx |
3 |
4 |
|
|
q 2 |
|
max Mx |
ql |
2 |
5 |
|
16 ; |
|
||||||
|
128 |
||||||||
|
|
4 |
|
|
0 |
|
|
|
|
Рассмотрим случай более сложной расчетной схемы, которая состоит из нескольких стержней, соединенных жестко. Такая стержневая система называется рамой.
Различают плоские и пространственные рамы. Они различаются количеством внутренних силовых факторов, возникающих в поперечных сечениях стержней. Если в плоской раме возникают не более трех усилий, то в пространственной их может быть до шести.
Пример 2: Плоская рама (рис.7). Пусть = qa, M = qa2
Все, что было рассмотрено в примере 1 остается справедливым и в более сложных расчетных схемах, кроме указанного уже количества силовых факторов в поперечном сечении.
1. При выборе системы координат, как и в примере 1, для верхнего горизонтального стержня начало координат совместим с левым крайним сечением, ось ОУ направим вверх, ось ОZ вправо. На вертикальном стержне ось ОZ совместим с осью стержня с началом в точке А. Точка А является общей точкой горизонтального и вертикального стержней и, чтобы в этой точке не получилось два одноименных сечения ( два левых или два правых), ось ОZ должна быть направлена вниз. Таким образом, система осей ZОУ горизонтального стержня на вертикальном должна быть повернута по часовой стрелке и ось ОZ будет направлена вниз, а ось ОУ вправо. Точно также на нижнем горизонтальном стержне получим направление ОZ – влево, а ОУ – вниз, т.е. система осей по всему контуру расчетной схемы движется в одном направлении.
В нашем случае будет четыре силовых участка:
. о z а; II. а z 4а; Ш. о z 2а; IV. о z 1,5а.
2. На каждом участке последовательно выполняем комплекс действий метода сечений (РОЗУ). Так, рассекая на четвертом участке, отбрасываем одну часть, которая в закреплении содержит три неизвестных реакции внешних связей. На рассматриваемую часть, (рис. 7а),
12
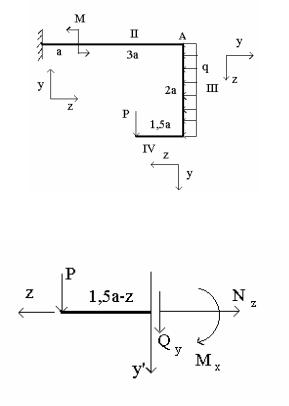
действует внешняя сила Р и внутренние усилия в сечении, которые направляем так, как это соответствует правому сечению, т.к. ось ОZ является внутренней нормалью по отношению к рассматриваемой части. Из равновесия рассматриваемой части находим:
о z 1,5а
Nz = 0; Qy = -P = -qa; |
Mx = P (1,5a – z) = qa (1,5а – z). |
Рис. 7
Рис. 7а Аналогичные действия проводим и на других участках (рис. 7 б,в,г).
о z 2а
Nz = P = qa; Qy = q (2a – z); Mx = P 1,5a – q (2a – z)2 / 2;
13
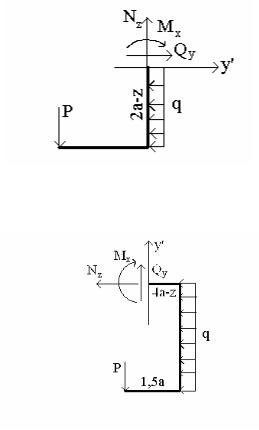
Рис.7б
а z 4а
Nz = -2qa; Qy = P = qa; Mx = qa (z – 2,5a) – 2qa2
Рис.7в
о z а
Nz = -2qa; Qy = P = qa; Mx = -qa (2,5 – z) – 2qa2 + M
14
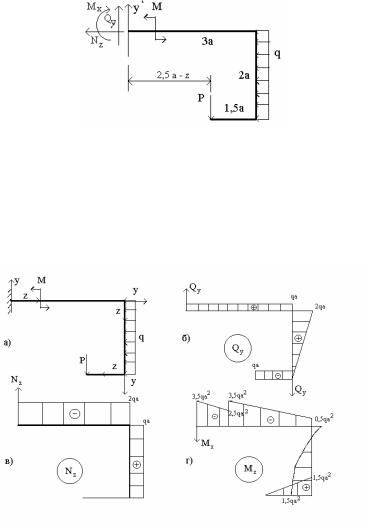
Рис.7г
Для графического изображения полученных функций внутренних усилий необходимо вычертить три контура расчетной схемы ( по одной для каждого внутреннего усилия). На каждом стержне ось абсцисс графика совмещаем с осью ОZ, а ось ординат Nz и Qy с осью ОУ. Ось ординат изгибающего момента Mx совмещаем с отрицательным направлением ОУ, как и в примере 1, (рис. 8 а,б,в, г)
Рис.8
Пример 3.: Рассмотрим пространственную раму (рис.9). Три стержня соединены жестко под прямыми углами. Пусть а = в = с,
2 2 1
15
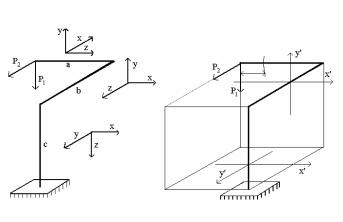
Рис.9 |
Рис.10 |
1. Также как и в предыдущем примере введем систему прямоугольных координат. Так как стержни соединены под прямыми углами, оси координат должны быть параллельны или перпендикулярны стержням. Так для стержня «а» ось ОZ совмещается с осью стержня, ось ОУ перпендикулярна оси стержня, а ось ОХ – параллельна среднему стержню. Начало координат совмещаем с левым крайним сечением стержня «а». На участке «в» эту же тройку осей получим путем поворота по часовой стрелки вокруг оси ОУ (вокруг оси перпендикулярной плоскости «ав») так, чтобы ось ОZ совместилась с осью стержня «в» , а ее начало было бы на границе стержней «а» и «в». При переходе от «в» к «с» поворот осей производим вокруг оси ОХ так, чтобы ось ОZ была направлена вниз (рис.9). В выбранной таким образом системе координат запишем границы силовых участков:
I. о z а; II. о z в; III. о z с.
2. На каждом участке определяем внутренние усилия выполняя комплекс действий (РОЗУ). Для лучшего видения пространства расчетную схему можно пунктирными линиями достроить до параллелепипеда (рис.10).
При замене действия отброшенной части (она содержит неизвестные в жесткой заделке), определив тип сечения (левое или правое), можно приложить все шесть силовых факторов и , составив шесть уравнений равновесия, найти отличные от нуля. В нашем случае нагрузка столь простая, что можно провести предварительный анализ и установить какие из силовых факторов будут отличными от нуля. Так,
16
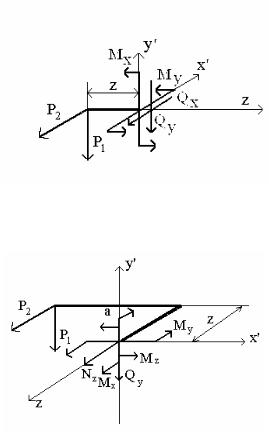
рассматривая сечение на участке о z а, видим (рис.10), что Р1 и Р 2
перпендикулярны оси ОZ и пересекают ее, следовательно, Mz = 0, Nz = 0. Поэтому в сечении имеем Qx, Qy, My, Mx (рис. 10а).
Qx P2 ; |
Qy P1; |
Mx P1 z; |
My P2 z |
|
Рис.10а |
|
|
Nz P2; Qy P1; Mz P1 a; Mx P1 z; My P2 a
Рис.10 б
На втором участке о z в такой анализ показывает (рис.10 б),
что Р2 проектируется на OZ, следовательноNz 0; P1проецируется на
17
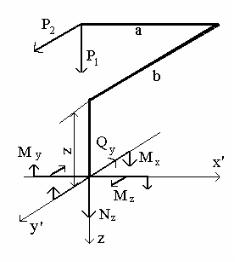
ось ОУ1 – Qy 0, Qx = 0, так как на ось ОХ1 не проектируется ни од-
на из сил. Mx 0, т.к. Р1 перпендикулярна ОХ1 и не пересекает ее.
Му 0, т.к. Р2 перпендикулярна ОУ1 и не пересекает ее. Мz 0, т.к.
Р1 перпендикулярна ОZ и не пересекает ее.
На третьем участке о z с аналогичный анализ показывает, что только Qx = 0 (рис. 10в).
Nz P1; |
Qy P2; |
Mz P2 a; |
Mx P1 b P2 z P1 b 2P1 z; My P1 a
Рис.10 в
Для построения графиков внутренних усилий заготовим для каждого внутреннего усилия свою нулевую линию в виде контура расчетной схемы. На каждом стержне соответствующее усилие изображаем обычным порядком, т.е. ось Qу, совмещаем с осью ОУ, ось Qх совмещаем с осью ОХ, ось My с отрицательной осью ОХ, ось Мx совмещаем с отрицательной осью ОY. Оси графика Nz и Mz совмещаются с осью ОХ или ОУ. Результат представлен на рис. 11.
18
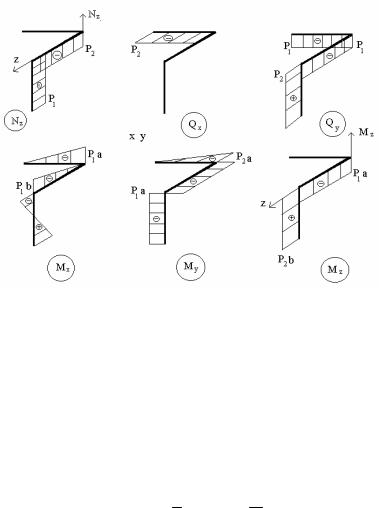
Рис. 11
Определение внутренних усилий по направлению внешних нагрузок.
Для плоской системы выражения внутренних усилий удобно записывать как суммы проекций и суммы моментов относительно рассматриваемого сечения всех внешних нагрузок, расположенных по од-
ну сторону сечения. Но т.к. R R и M M , то для устранения
неоднозначности результата, необходимо ввести правила знаков для записи сумм проекций и сумм моментов внешних сил, действующих по разные стороны сечения.
1. Продольная сила Nz равна сумме проекций на ось стержня всех внешних сил, расположенных по одну сторону от сечения, запи-
19
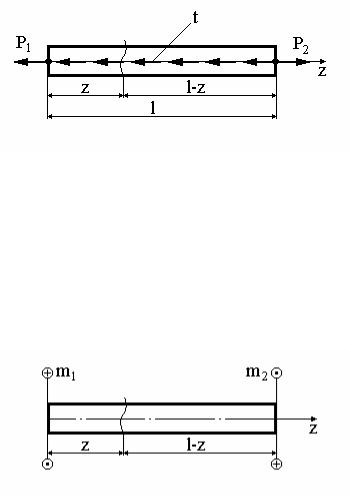
санных со знаком +, если сила направлена от сечения, и со знаком -, если внешняя сила направлена к сечению. (Рис.12).
Рис.12
Так как стержень находится в равновесии, то
P1 t P2 0 P2 P1 t
Nzлев P1 tz
По правилу 1
Nправ P2 t( z) P1 tz
2. Крутящий момент Mz равен сумме моментов относительно оси стержня внешних сил по одну сторону от сечения, записанных со знаком +, если сила (момент) при взгляде со стороны сечения вращается по часовой стрелке, и со знаком -, если вращается против часовой стрелки (Рис.13).
Рис. 13
Так как стержень находится в равновесии m1 m2 0 m1 m2
По правилу 2 M лев m |
M прав m |
2 |
|
z |
1 |
z |
|
20
