Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Киевский национальный университет им. Т. Шевченко

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ИсследованиеОпераций

.pdf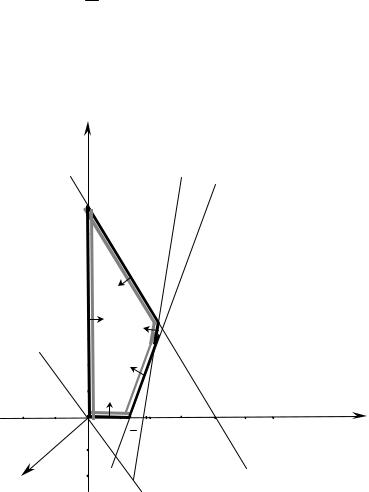

Скачиваний:

Добавлен:

07.03.2016

Размер:

1.89 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 115 6 7 8 9 10 11 > Следующая >>>

Оскільки, x j ≥

nr = (−2;−2)

x	= 11 −6 x	3	+ x	5	,
1		3		5	(5.6)
x2	= 8 −2x3 − x5 ,				(5.6)
	= 4 −3x3 + x5 .
x4	= 4 −3x3 + x5 .

0, j = 1,5 , то

11 −6 x3 + x5 ≥ 0,

8 −2x3 − x5 ≥ 0,4 −3x3 + x5 ≥ 0.

x3 ≥ 0, x5 ≥ 0.

6 x3 − x5 = 11

8	3x3 − x5 = 4

1			x3
			x3
1	4	11	4
	3	6

2x3 + x5 = 8

− 2x3 − 2x5 = L*max

Рис.5.6.

Тому, остаточно, отримуємо таку загальну задачу ЛП

L = −2x3 −2x5 → max,

6 x3 − x5 ≤11,

+ x5 ≤ 8,

2x3

− x5 ≤ 4,

3x3

x3 ≥0, x5 ≥0,

яку розв'язуємо графічно (див. рис.5.6).

Отже, максимальне значення L*

=0 цільової функції

L = −2x

−2x

max

досягається у точці

(x3* , x5* ) = O = (0,0)

координатної площини

x3Ox5 ,

тобто

x3 =0, x5 =0 .

Значення координат

x* , x* , x*

оптимального розв'язку

вихідної

задачі обчислюємо за формулами (5.6): x*

=11, x* = 8,

x* = 4 .

Тоді оптимальний розв'язок вихідної задачі та її оптимальне

значення відповідно рівні вектору

X *

= (11;8;0;4;0) та числу Z *

= −L*

=0 .

min

max

5.4. Вправи.

1)	Розв'язати графічно такі задачі лінійного
	z = x1 −2x2 (min),	2)	z = x1 + x2 (max),

x		− x		≤1,
	1		2	≥ 2,
x1		+ x2
x		−2x		2	≤0,
	1
x		≥0; x			2	≥0;
	1

4)z = 5x1 +3x2 (max),

3x1 +5x2 ≤15,5x1 +2x2 ≤10,

x1 ≥0; x2 ≥0;

7)z = 2x1 + x2 (min),

3x1 − x2 ≥ 1,

− x1 + 3x2 ≥ 5;

x1 +2x2 ≤10,

x1 +2x2 ≥ 2,

2x1 + x2 ≤10,

x1 ≥0; x2 ≥0;

5)z = 2x1 +3x2 (max),

3x1 +2x2 ≤6,

x1 + x2 ≥1,x1 ≥0; x2 ≥0;

8)z = x1 − x2 (max),

x1 − x2 ≤ 1,x1 − x2 ≥ 1,x1 ≥0; x2 ≥ 0;

програмування:

3)z = x1 +3x2 (max),

x1 − x2 ≤1,

2x1 + x2 ≤ 2,x1 − x2 ≥0,

x1 ≥0; x2 ≥0;

6)z = 2x1 +3x2 (min),

3x1 +2x2 ≥6,

x1 +4x2 ≥ 4,x1 ≥0; x2 ≥0;

9)z = 2x1 + x2 (max),

− 2x1 + x2 ≤ 2,x1 − x2 ≥ 2,x1 ≥0; x2 ≥0;

10)z = 4x1 −2x2 + x3 − x4 (max),

x1 − x2 +4x3 −2x4 = 2,3x1 +2x2 − x3 +4x4 = 3,

xi ≥0(i =1,...,4);

12)z = −4x1 +3x2 + x4 − x5 (max),

	2x1 − x2 − x3													= −1,
	x	−3x		2			− x		4					= −13,
	1			2					4
									+ x5					= 26,
	4x1 + x2								+ x5					= 26,
	x	−3x		2							+ x			=0,
	1			2									6
		≥0(i =1,...,6);
	xi	≥0(i =1,...,6);
14)	z = x1 − x2 (max),
	4x	1	−3x		2	− x	3	+ x		4	+ x	5	=6,
		1			2		3			4		5
	x1	+4x2 + x3								+ x5 =15,
	2x	1	−4x		2	− x	3	+ x		4		= −3,
		1			2		3			4
	x	≥0(i =1,...,5);
	i

11)z = x1 +2x2 + x3 − x4 −6(min),

− x	1	+5x	2	+ x	3	+ x	4	+ x	5	=10,
	1		2		3		4		5
2x1 − x2 + x3 −3x4										=6,
	10x2 + x3 +2x4							+3x5 = 25,
	10x2 + x3 +2x4							+3x5 = 25,

xi ≥0(i =1,...,5);

13)z = −3x1 +2x2 −3x4 − x5 (max),

2x1 − x2 − x3 + x4

= −1,

−3x

+ x

= −13,

− x4

+ x5

= 26,

4x1 + x2

−3x

− x

=0,

≥0(i =1,...,6);

15)

z = x1 − x2 (max),

2x1 − x2

+ x5 + x6 =6,

+2x

+ x

= 25,

+ x5

= −9,

2x1 −3x2 − x3

6 x2 + x3 + x4

= 36,

≥0(i =1,...,6).

6. Симплекс-алгоритм для розв'язування канонічних задач лінійного програмування.

6.1 Основні факти.

Теорема 5.1 (про оптимальні розв'язки задачі ЛП і вершини її допустимої області).

1. Якщо цільова функція задачі ЛП
	Τ	n
	Τ	x : ∑x j Aj = A0		(6.1)
max c		x : ∑x j Aj = A0	, x ≥ 0	(6.1)
		j=1

набуває максимального значення в деякій допустимій точці x* D ={x Rn , Ax = a0 , x ≥ 0} , то вона набуває цього ж значення і в

деякій вершині D .

2. Якщо цільова функція задачі (6.1) набуває максимального значення у кількох вершинах допустимої області D , то вона набуває

цього значення і в довільній їх опуклій комбінації.

Теорема 6.2 (про опорні розв'язки задачі ЛП і вершини її допустимої області).

Допустимий розв'язок задачі ЛП (6.1) є вершиною її допустимої області D тоді і тільки тоді, коли він базисний

(опорний).

Зауваження 6.1.

За теоремою 1 оптимальний розв'язок задачі ЛП, якщо він існує, є вершиною допустимої області задачі.

За теоремою 2 кожній вершині допустимої області задачі ЛП відповідає опорний (базисний, допустимий) розв'язок системи

n
∑x j Aj = A0 , x ≥ 0 .	(6.2)

j=1

Отже перехід він однієї вершини допустимої області D до іншої означає перехід від одного опорного розв'язку системи (6.2) до іншого.

У симплекс-методі здійснюються послідовні переходи від одного опорного розв'язку (плану) задачі ЛП до іншого так, щоб базис наступного опорного плану відрізнявся від базису попереднього тільки одним вектором.

Лема 6.1 (про заміну вектора у базисі)
Нехай A1 , A2 ,..., An система					m -вимірних векторів ( m < n )						рангу
m і x j ≥ 0, j = 1,..., 5.			деякий її базис.
Система			векторів	B′ ={Ai		, Ai	,..., Ai	, Ak Ai ,...,	Ai	} ,	де
					1	2	l−1	l+1		m
Ak ( k ≠ is ; s =		) –	небазисний		вектор,		буде	базисом		системи
Ak ( k ≠ is ; s =	1, m	) –	небазисний		вектор,		буде	базисом		системи
{A1 , A2 ,..., An } , тоді і тільки тоді коли у розкладі
		Ak =α1k Ai1 +... +αlk Ail			+... +αmk Aim				(6.3)
вектора Ak по базису B коефіцієнт αlk						задовольняє умову
		αlk ≠ 0 .							(6.4)

Теорема 6.3 (достатні умови переходу до кращого опорного розв'язку задачі ЛП).

Нехай x = (α10 ,α20	,...,αm0	,0,...,0)T	відомий опорний розв'язок
		123
		n−m

задачі (6.1), B = [ A1 , A2 ,..., Am ] відповідна йому базисна матриця.

Якщо	існує		небазисний	вектор	Ak	у	системі
						m
{A1 , A2 ,..., Am , Am+1 ,..., An } , для якого ∆k < 0				( ∆s = (cб,αs ) −cs = ∑ciαis −cs ), і у
розкладі якого						i=1
розкладі якого							(6.5)
	Ak	=α1k Ai1 +... +αlk Ail +... +αmk Aim					(6.5)
по базису B	існує принаймні один додатний коефіцієнт αik > 0 , то
заміна вектором		Ak	базисного вектора з		порядковим		номером

l = arg min α

{i:αik >0} α

i0	у базисі	B	приведе до	нового базису
ik

B′ = [ A1 ,..., Al−1 , Ak Al+1 ,..., Am ] ,

якому

відповідає,

новий базисний

розв'язок x

′

,0,...,0)

, де

= (α10 ,...,αl−1,0 ,0,αl+1,0 ,...,αm0 ,0,...,0,αl0

αi′0 =αi0

− αl0

αik ,i =

1, m

,i ≠ l,

(6.6)

αl′0 =

αl0

і для якого

cT x ≤ cT x′ ,

зокрема,

cT x < cT x′ ,

якщо задача (6.1)

невироджена.

Зауваження 6.2.

Якщо система (2) приведена до канонічної форми

∑ei xi +

∑αj x j = α0 , α0

≥0, x ≥0 ,

(6.7)

i=1

j=m+1

де e

= B−1 A

, i =

= B−1 A

, j =

; α

= B−1 A

, то заміну вектора

1, m

m +1, n

el у канонічному базисі вектором αk практично здійснюють методом повного виключення Жордана-Гаусса, виконуючи один крок повного виключення з ведучим елементом αlk на розширеній матриці α = B−1 A

1		0 ..	0 ..	0	α	1,m+1
	0	1 ..	0 ..	0		1,m+1
	0	1 ..	0 ..	0	α2,m+1

α = ... ... .. ... .. ... .........
	0	0 ..	1 ..	0	αl,m+1

... ... .. ... .. ... .........
	0	0 ..	0 ..	1	α	m,m+1
						m,m+1

коефіцієнтів канонічної системи (6.7).

..	α	1k	..	α	1n	α	10

..	α2k		..	α2n		α20
.. .....			.. .....			.....

..	αlk		..	α1n		αl0
.. .....			.. .....			.....

..	α	mk	..	α	mn	α	m0

Теорема 6.4 (ознака оптимальності опорного розв'язку задачі ЛП).

Якщо для деякого опорного	розв'язку x = (x1 , x2 ,..., xm ,0,...,0)T
задачі (6.1) всі симплекс-різниці невід'ємні
m
∆ j = (cб , αj ) − c j = ∑ciαij	− c j ≥ 0 ,
i=1
то x – оптимальний розв'язок задачі (6.1).

Теорема 6.5 (ознака необмеженості цільової функції на допустимій області задачі ЛП).

Якщо для деякого опорного розв'язку	x	задачі (6.1), якому
відповідає базис B =[ Ai1 , Ai2 ,..., Aim ] , існує принаймні один небазисний
m
вектор Ak , для якого ∆k = (cб, αk ) −ck = ∑cisαik −ck	<0	і αik ≤0 , i =	1, m	, то
s=1

цільова функція задачі (6.1) необмежена зверху на її допустимій області.

6.2. Алгоритм симплекс-методу.

Зауваження 6.3.

Не обмежуючи загальності можна вважати, що початковому опорному плану x0 задачі ЛП

n
∑c j x j → max		(6.8)
j=1
n
∑x j Aj = A0 ,		(6.9)
j=1
		(6.10)
x j ≥0, j =	1, n

відповідає базис B =[ A1 , A2 ,..., Am ] . Тоді канонічна форма обмежень (6.9),, яка відповідає базису B , має вигляд

xi + ∑αij x j

=αi0

≥ 0,

(6.11)

j=m+1

x j ≥ 0, j =

1, n

Вона і визначає початковий опорний план

x0 = (α

,α

,...,α

,0,...,0)T .

123

n−m

Коефіцієнти канонічної

форми

αij ,

i =

j =0;

1, m

m +1, n

координатами векторів αj ,

j =0;

в одиничному

базисі e1 ,e2 ,...,em

m +1, n

системи	{A , A		,..., A } ,	α		= B−1 A , j =0;		або коефіцієнтами розкладу
системи	{A , A		,..., A } ,	α	j	= B−1 A , j =0;	m +1, n	або коефіцієнтами розкладу
	1	2	n		j
								m
векторів	Aj по неканонічному базису B =[ A1 , A2 ,..., Am ] , Aj = ∑αij Ai .
								j=1
	Нехай	x s − поточний опорний план задачі (6.8)−(6.10), αs −матриця

коефіцієнтів канонічної форми обмежень (6.9), що визначає x s .


Симплекс-алгоритм для канонічної задачі ЛП.
	1. Обчислити симплекс-оцінки ∆sj = (cбs ,αsj ) −c j небазисних векторів
Aj	(для базисних ∆sj =0 ). Перейти до наступного пункту.
	2. Перевірити умову:			∆sj ≥0 , j =		. Якщо умова виконується, то −
					1, n
кінець обчислень, поточний базисний допустимий розв'язок							x s	є
оптимальним. В іншому випадку − перейти до наступного пункту.
	3. Перевірити умову:			небазисна змінна xk для якої			∆sk <0	і
αiks	≤ 0 , i =		. Якщо умова виконується, то − кінець обчислень,				цільова
		1, m

функція задачі необмежена на допустимій області зверху. В іншому випадку перейти до наступного пункту.

4. Знайти номер k = arg min ∆sj найменшої від'ємної симплекс-різниці
		{ j:∆sj <0}
( k − номер	направляючого	стовпця	симплекс-перетворення, вектор Ak
повинен бути введений у базис). Перейти до наступного пункту.
5.	Знайти номер	l = arg min	αs	направляючого рядка симплекс-
			io
		{i:αiks >0}	αiks

перетворення. Перейти до наступного пункту.

6. Виконати крок повного виключення методом Жордана-Гаусса на розширеній матриці [ αs , α0s ] канонічної системи рівнянь-обмежень з l -м направляючим рядком і k -м направляючим стовпцем (ведучий елемент –

αlks ). Перейти до пункту 1.

Кінець алгоритму.

Проміжні результати обчислень зручно зберігати у так званій симплекс-таблиці (див. таблицю 4).

В ній позначено: i – номер рядка матриці α ; cб – вектор коефіцієнтів цільової функції при базисних змінних; xб – вектор базисних змінних; A0 – вектор правих частин системи рівнянь-обмежень;

Таблиця 4.

cб

xб

...

cm+1

…

θi

...

Am+1

…

α10

...

α1m+1

…

α1n

α20

...

α2m+1

…

α2n

…

...

αm0

...

αmm+1

…

αmn

∆ j

L( x)

...

∆m+1

…

∆n

A j ( j =

) – вектори умов;

θi =

αi0

; ∆ j = (cб , αj ) −c j ,

j =

–

симплекс-

1, n

різниці;

c j ( j =

) – коефіцієнти цільової функції.

1, n

6.3. Приклади.

Приклад 1. Розв’язати симплекс-методом задачу ЛП:

L = x1 − x2 → max

−2x1 + x2 + x3

= 3,

−2x

+ x

= 2,

+ x

= 5,

≥0, j =

1,5.

Розв’язування. Результати обчислень заносимо у симплекс-таблицю (див.

таблицю 5).

Обчисливши симплекс-різниці на першому кроці, з’ясовуємо,що

початковий опорний план			x0 = (0,0,2,2,5)T ,		для якого	L(x0 )= 0 , не	є
оптимальним,	оскільки	∆1 = −1 <0 . Тому		до	базису вводимо вектор		A1
(позначений	стрілкою).	За	мінімумом	θi − відношень		визначаємо

направляючий рядок симплекс-перетворення (другий), позначаємо його

стрілкою біля змінної	x4 у стовпчику xб . Симплекс-перетворенням з базису
буде виведений вектор A4 . Виконуємо симплекс-перетворення елементів
таблиці з ведучим	елементом α12 =1	(клітина	виділена півтоном).
Отримаємо опорний план x1 = (2,0,6,0,3)T ,		для якого	L(x1 )= 2 . Переходимо

до другого кроку.

Таблиця 5.

	і	cб	xб		A0	1	–1	0	0			0		θi
	і	cб	xб		A0	A1	A2	A3	A4			A5		θi
						A1	A2	A3	A4			A5
	1	0	x3		2	–2	1	1	0			0
	2	0	← x4		2	1	–2	0	1			0		2
	3	0	x5		5	1	1	0	0			1		5
		∆ j	L		0	–1 ↑	1	0	0			0
	1	0	x3		6	0	–3	1	2			0
	2	1	x1		2	1	–2	0	1			0
	3	0	← x5		3	0	3	0	–1			1
		∆ j	L		2	0	–1 ↑	0	1			0
	1	0	x3		9	0	0	1	1			1
	2	1	x1		4	1	0	0	1	3		2	3
										3			3
	3	–1	x2		1	0	1	0	− 1		3	1	3
											3		3
		∆ j	L		3	0	0	0	2	3		1	3
										3			3
		На другому кроці				з’ясовуємо, що		∆2 = −1 <0 , тобто опорний план
x1 = (2,0,6,0,3)T				неоптимальний.			Виконуємо		симплекс-перетворення

елементів таблиці з ведучим елементом α32 = 3 , при цьому направляючий

третій рядок перетворення визначається без додаткових обчислень за єдиним додатним елементом α32 = 3 вектора A2 , що вводиться в базис.

Отримаємо опорний план x 2 = (4,1,9,0,0)T , для якого L(x1 )= 3 . Всі

симплекс-різниці відносно базису цього плану невід’ємні (клітини останнього рядка таблиці, в які вони занесені, виділені напівтоном), тому він оптимальний. Отже, оптимальним розв’язком задачі є вектор

x* = (4,1,9,0,0)T , а її оптимальне значення рівне L(x* )= 3 . Приклад 2. Розв’язати симплекс-методом задачу ЛП:

L = 2x1 + x2 → max,
	x	−	2x	≤ 1, x	− x	2	≤ 2,
	1		2	1		2

− 2x1 + x2 ≤ 2, x1 ≥ 0, x2 ≥ 0.

Розв’язування.Зводимо задачу до канонічної форми: 49

L = 2x1 + x2						→ max,
x1 −2x2 + x3									=1,
						+ x4			= 2,
−2x1 + x2						+ x4			= 2,
		x	1	− x	2		+ x	5	= 2,
			1		2			5
x		≥ 0, j			=
x	j	≥ 0, j			=	1,5.
	j

Результати обчислень заносимо у симплекс-таблицю (див. таблицю 6).

Таблиця 6.

і	cб	xб	A0	2	1	0	0	0	θi
і	cб	xб	A0	A1	A2	A3	A4	A5	θi
				A1	A2	A3	A4	A5
1	0	← x3	1	1	–2	1	0	0	1
2	0	x4	2	–2	1	0	1	0
3	0	x5	2	1	–1	0	0	1	2
	∆ j	L	0	–2 ↑	–1	0	0	0
1	2	x1	1	1	–3	1	0	0
2	0	x4	4	0	–2	2	1	0
3	0	← x5	1	0	1	–1	0	1
	∆ j	L	2	0	–5 ↑	2	0	0
1	2	x1	3	1	0	–1	0	2	1
2	0	x4	7	0	0	–1	1	3
3	1	x2	1	0	1	–1	0	1	2
	∆ j	L	6	0	0	–3	0	4

До перших двох симплекс-перетворень додаткові коментарі непотрібні (клітини, в яких стоять їх ведучі елементи, виділені напівтоном).

На останньому кроці від’ємна симплекс-різниця		∆3 = −3 <0
відповідає вектору	A = (−1, −1, −1)T з від’ємними координатами	(стовпчик
	3

таблиці виділений напівтоном), тому задача нерозв’язна − її цільова функція необмежена зверху на допустимій множині.

6.4.Вправи.

Розв'язати симплекс-методом задачі ЛП, при можливості дати геометричну інтерпретацію процесу розв'язування:

<<< < Предыдущая 1 2 3 45 / 115 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.03.201558.07 Кб184Инструкция по учету Агентуры.docx
#
07.03.2016577.32 Кб15Интроверт.pdf
#
19.03.201545.04 Кб9Информационные.docx
#
08.07.20191.67 Mб1Иоанна Хмелевская -- (Nie)Boszczyk maz_POL.doc
#
19.03.201573.33 Кб5иппв.docx
#
07.03.20161.89 Mб17ИсследованиеОпераций.pdf
#
19.03.201554.77 Кб6Исторія модуль 2.docx
#
28.04.2019197.84 Кб1Историография. Шпоры.docx
#
23.12.2018332.8 Кб4история 2 - 2003.doc
#
19.03.2015199.17 Кб5история дипломатии том 2 ГЛАВА 7.doc
#
07.03.20162.04 Mб52История Медицины. Т.1..pdf