§ 3. Матрица перехода от базиса к базису
Пусть
b
= {b1
, … , bn}
– базис
n-мерного
векторного пространства V
над полем F.
Тогда L(b)
= V,
так что любой вектор v
V
является линейной комбинацией базисных
векторов: v
= 1b1+…+nbn
. Напомним,
что скаляры 1
, … , n
F называются
координатами
вектора v
в базисе b
, а вектор-столбец
nF
– координатным
столбцом вектора v
в базисе b
и обозначается через [v]b
. Было доказано, что координатные столбцы
удовлетворяют следующим очевидным
свойствам:
10. [0]b = 0 nF.
20. u, v V [u+v]b = [u]b + [v]b .
30. F v V [v]b = [v]b .
Пусть теперь e = {e1 , … , en} и f = {f1 , … , fn} – два базиса векторного пространства V. Тогда каждый вектор fi однозначно разлагается по базису e : fi = e1t1i + … + entni (1 i n). Таким образом, существует однозначно определённая матрица Te,f = (tij) M(n, F) со свойством f = eTe,f . При этом по свойству 150 матричного символизма Te,f GL(n, F). Матрица Te,f называется матрицей перехода от базиса e к базису f.
Из определения немедленно следует, что fi = e1t1i + … + entni = et(i). Таким образом, t(i) = [fi]e и Te,f = ([f1]e , … , [fn]e).
Примеры: 1. Пусть e = (e1 , e2 , e3) – произвольный базис векторного пространства V , f = (e1 – e3 , e1 + e2 , 2e2 + e3).
Тогда
f
= (e1
, e2
, e3)
. При этом матрица Te,
f
=
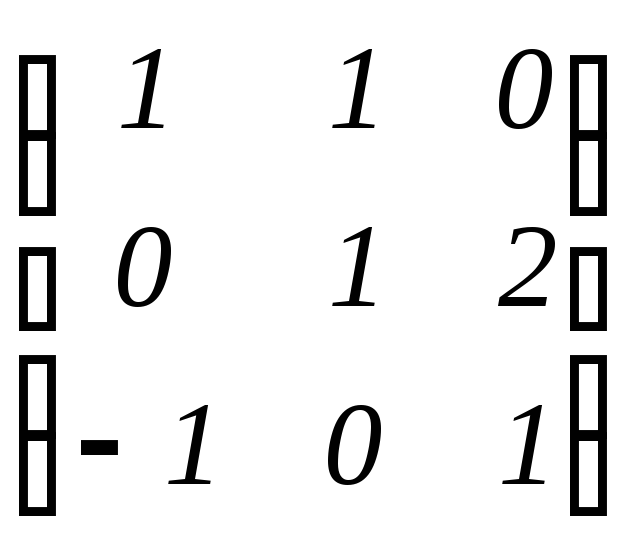невырождена, т.е. f
– базис V,
а Te,
f –
матрица перехода от e
к f.
2. Пусть V = R n, e = (e1 , … , en) и f = (f1 , … , fn) – два базиса. Известно, столбец [fj] находится из системы уравнений (e1t , … , ent)[fi]e = fit . Поэтому матрица перехода Te,f = ([f1]e , … , [fn]e) удовлетворяет матричному уравнению (e1t , … , ent)Te,f = (f1t , … , f1t).
3. Если же V = nR , e = (e1 , … , en) и f = (f1 , … , fn) – два базиса V, то аналогично предыдущему можно получить, что матрица Te,f однозначно определяется системой линейных уравнений (e1 , … , en)Te,f = (f1 , … , fn).
4.
Пусть V
= R3,
e
= ((1; 0; 1), (–1; 1; 0), (0; 0; 1)), f
= ((0; 0; –1), (0; 1; 1), (2; 0; 0)).
Для нахождения матрицы перехода Te,f
записываем
систему
Te,f
=
,
решая которую, получаем
Te,f
=
.
Свойства матрицы перехода
10. Для любого базиса e = (e1 , … , en) векторного пространства V выполнено Te,e = In .
Действительно, e = eIn .
20. Для любых двух базисов e = (e1 , … , en) и f = (f1 , … , fn) векторного пространства V матрицы перехода Te, f и Tf, e связаны соотношением Tf, e = Te, f–1 .
В самом деле, если f = eTe, f , то учитывая обратимость матрицы Te, f , получим e = eIn = eTe, f Te, f–1 = fTe, f–1 . С другой стороны, e = fTf, e , так что Tf, e = Te, f–1 .
30. Для любых трёх базисов e = (e1 , … , en) , f = (f1 , … , fn) и g = (g1 , … , gn) векторного пространства V матрицы перехода Te,f , Tf,g и Te,g связаны соотношением Te, g = Te, f Tf, g .
Действительно, g = fTf,g , f = eTe,f . Поэтому
eTe,g = g = fTf,g = (eTe,f)Tf,g = e(Te, f Tf, g),
и значит, Te, g = Te, f Tf, g .