§ 7. Собственные числа и собственные векторы линейного оператора

Пусть V – векторное пространство над полем F,  : V  V – линейный оператор. Элемент   F называется собственным числом (или значением) линейного оператора  , если существует такой ненулевой вектор v  V, что (v) = v. При этом вектор v  V \ {0} с вышеуказанным свойством называют собственным вектором линейного оператора  , соответствующим (или отвечающим) собственному значению  .

Нетрудно видеть, что любой собственный вектор v порождает одномерное -инвариантное подпространство W = L(v): (v) = (v) = v  W. С другой стороны, если W – одномерное -инвариантное подпространство и v  W \ {0}, то W = L(v) и (v) = v для некоторого   F, т.е. v – собственный вектор для  . Таким образом, изучение собственных векторов линейного оператора  эквивалентно изучению его одномерных инвариантных подпространств.

С понятиями собственного числа и собственного вектора линейного оператора тесно связаны аналогичные понятия для матриц. Пусть A – квадратная (nn)-матрица над полем F. Элемент   F называется собственным числом (или значением) матрицы А, если существует такой вектор v  ⁿF \ {0}, что Av =  v. При этом ненулевой вектор v с вышеуказанным свойством называют собственным вектором матрицы А, соответствующим (или отвечающим) собственному значению  .

Множество всех собственных чисел линейного оператора  : V  V (или матрицы A  M(n, F)) называют спектром линейного оператора  (или матрицы A) и обозначают через Sp() (или Sp(A)). Задачу отыскания всех собственных чисел и соответствующих им собственных векторов линейного оператора  (или матрицы A) называют спектральной задачей.

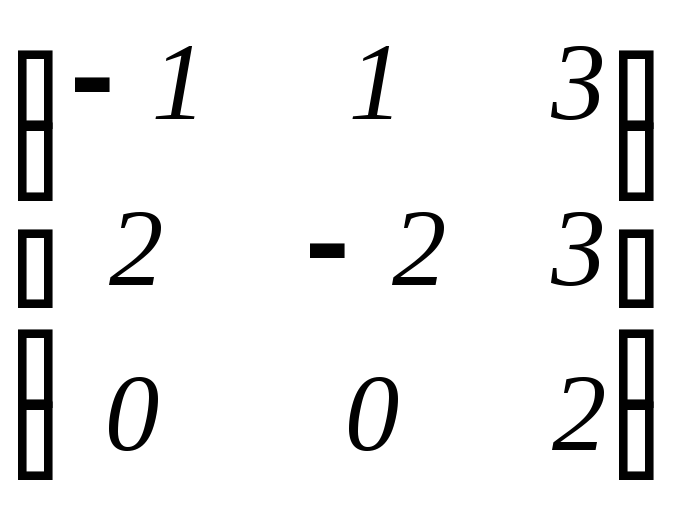
Примеры: 1. Матрица  M(3, R) имеет собственный вектор , отвечающий её собственному значению = 2, в чём нетрудно убедиться, вычислив .

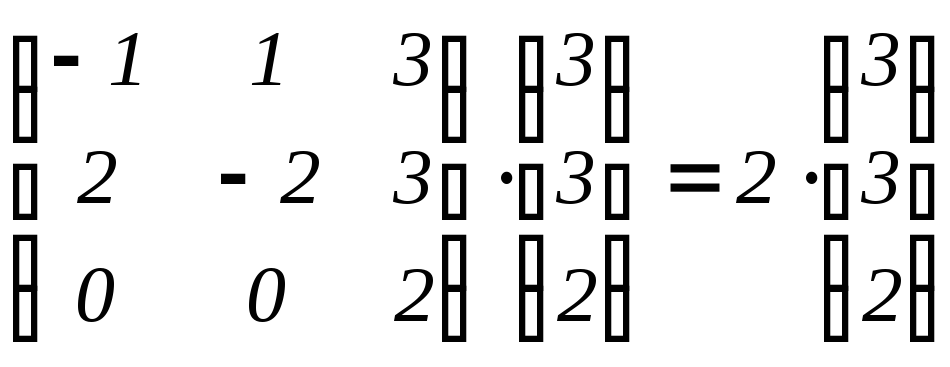2. Если в некотором базисе e₁ , e₂ , e₃ линейный оператор  : V  V имеет матрицу []_e предыдущего примера, то вектор 3e₁ + 3e₂ + 2e₃ является его собственным вектором. В самом деле,

(3e₁ + 3e₂ + 2e₃) = 3(e₁) + 3(e₂) + 2(e₃) =

= 3(–e₁ + 2e₂) + 3(e₁ – 2e₂) + 2(3e₁ + 3e₂ + 2e₃) =

= 6e₁ + 6e₂ + 4e₃ = 2(3e₁ + 3e₂ + 2e₃).

Этот собственный вектор соответствует собственному числу  = 2 линейного оператора  и его координатный столбец был найден в примере 1. У линейного оператора  есть ещё и другой собственный вектор: (–e₁ + 2e₂) = = –(e₁) + 2(e₂) = –(–e₁ + 2e₂) + 2(e₁ – 2e₂) = 3e₁ – 6e₂ = –3(–e₁ + 2e₂). Собственный вектор –e₁ + 2e₂ отвечает собственному значению  = 3. Как Вы думаете, будет ли оно являться собственным числом матрицы примера 1 ?

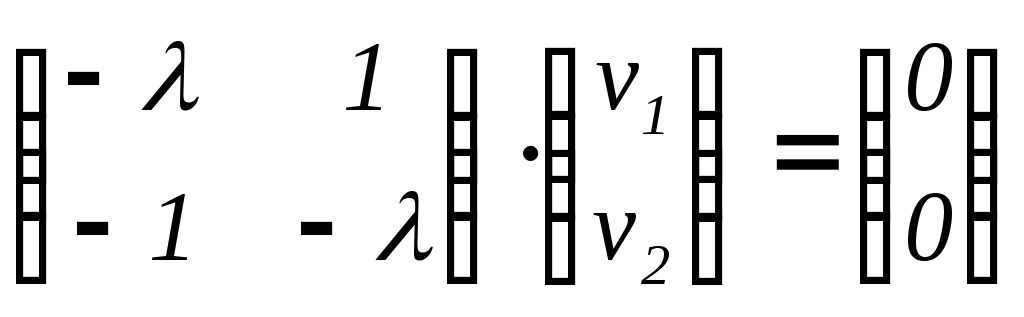3. Матрица А =  M(2, R) не имеет собственных чисел, а значит и собственных векторов. Действительно, если   R – собственное число матрицы А, то Аv = v, т.е. (A – I₂)v = 0. Таким образом, однородная система линейных уравнений имеет ненулевое решение. Значит det = 0, т.е. ² + 1 = 0. Это уравнение не имеет решений в поле R . Полученное противоречие показывает, что предположение о существовании собственного числа матрицы было не верным.

4. Следует отметить, что матрица предыдущего примера, рассматриваемая над полем комплексных чисел имеет два собственных числа i и –i . Первому из них отвечает собственный вектор , т.к. . Какой собственный вектор будет соответствовать второму собственному числу ?

5. Пусть R_ : V₂(O, R)  V₂(O, R) – линейный оператор поворота на угол  против часовой стрелки. Решим спектральную задачу для оператора R_ . Если R_(v) = v, то векторы R_(v) и v коллинеарны, что возможно лишь при  = k (k  Z) (?!).

С другой стороны, если  = 2k (k  Z), то R_(v) = v для любого вектора v  V₂(O, R). Таким образом, при  = 2k (k  Z), любой ненулевой вектор является собственным для оператора R_ и отвечает собственному значению  = 1. Если же  = (2k+1) (k  Z), то R_(v) = –v при любом векторе v  V₂(O, R). Таким образом, при  = (2k+1) (k  Z), любой ненулевой вектор является собственным для оператора R_ и отвечает собственному значению  = –1.

Итак, спектральная задача для оператора R_ имеет следующее решение: при   k (k  Z) у этого линейного оператора нет ни собственных чисел, ни собственных векторов; при  = 2k (k  Z) у него единственное собственное число  = 1, которому отвечает множество собственных векторов, состоящее из всех ненулевых векторов плоскости; при  = (2k+1) (k  Z) у него единственное собственное число  = –1, которому отвечает множество собственных векторов, состоящее из всех ненулевых векторов плоскости.

Теорема (о связи спектральных задач для линейного оператора и его матрицы). Пусть  – линейный оператор в конечномерном векторном пространстве V с базисом e = (e₁ , … , e_n). Тогда

1.    F   Sp()    Sp([]_e),

2. вектор v  V \ {0} является собственным вектором линейного оператора  , отвечающим собственному значению   Sp() тогда и только тогда, когда вектор [v]_e  ⁿF является собственным вектором матрицы оператора []_e , отвечающим собственному числу   Sp([]_e).

Доказательство. Оба утверждения будем доказывать одновременно. Пусть v  V \ {0} – собственный вектор линейного оператора , отвечающий собственному числу   Sp(). Это равносильно условию (v) = v, которое, в свою очередь, эквивалентно координатной форме записи []_e[v]_e = = [(v)]_e = [v]_e . При этом [v]_e  0  ⁿF , т.к. v = e[v]_e  0  V. Таким образом, [v]_e является собственным вектором матрицы []_e , соответствующим собственному значению   Sp([]_e).

Теорема доказана.

Теорема (о решении спектральной задачи для матрицы). Для любой матрицы A  M(n, F) справедливы следующие утверждения:

1.    F   Sp(A)  det(A – I_n) = 0,

2. если   Sp(A), то однородная система линейных уравнений (A – I_n)v = 0  ⁿF имеет ненулевые решения, множество которых совпадает с множеством собственных векторов, соответствующих собственному значению  .

Доказательство. Оба утверждения будем доказывать одновременно. Если   Sp(A) и v  ⁿF \ {0} – отвечающий  собственный вектор, то Av = v   Av – I_nv = 0  (A – I_n)v = 0. Последняя однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда определитель её основной матрицы нулевой: det(A – I_n) = 0.

Обратно, если   F и det(A – I_n) = 0, то однородная система линейных уравнений (A – I_n)v = 0 имеет ненулевое решение v  ⁿF \ {0}, которое удовлетворяет соотношению Av = v, т.е. является собственным вектором, соответствующим собственному числу  .

Теорема доказана.

Уравнение det(A – I_n) = 0, решениями которого являются собственные числа матрицы A (и только они), называется характеристическим уравнением матрицы А. Многочлен _А() = det(A – I_n) называют характеристическим многочленом матрицы А.

Доказанная теорема даёт алгоритм решения спектральной задачи для матрицы А:

I. Составление характеристического уравнения det(A – I_n) = 0.

II. Нахождение собственных чисел матрицы А – корней её характеристического уравнения.

III. Для каждого собственного числа _i нахождение собственных векторов, отвечающих этому числу, – как множества всех ненулевых решений однородной системы линейных уравнений (A – I_n)v = 0.

Для линейного оператора спектральная задача решается путём предварительного сведения её к спектральной задаче для матрицы этого оператора в подходящем образом выбранном базисе и заключительного нахождения собственных векторов по найденным их координатным столбцам.

Примеры: 1. Решим спектральную задачу для линейного оператора, заданного в пространстве R³ правилом (x; y; z) = (x + z; 2y; –x – z).

0. Выберем стандартный базис

e = (e₁ = (1; 0; 0), e₂ = (0; 1; 0), e₃ = (0; 0; 1))

пространства R³ и найдём матрицу A = []_e оператора в этом базисе.

Имеем (e₁) = (1; 0; 0) = (1; 0; –1) = e₁ – e₃ , (e₂) = (0; 1; 0) = = (0; 2; 0) = 2e₂ , (e₃) = (0; 0; 1) = (1; 0; –1) = e₁ – e₃ . Поэтому можно составить матрицу А = []_e = .

Решаем спектральную задачу для матрицы А.

I. Составляем характеристическое уравнение det(A – I_n) = 0.

det(A – I_n) = 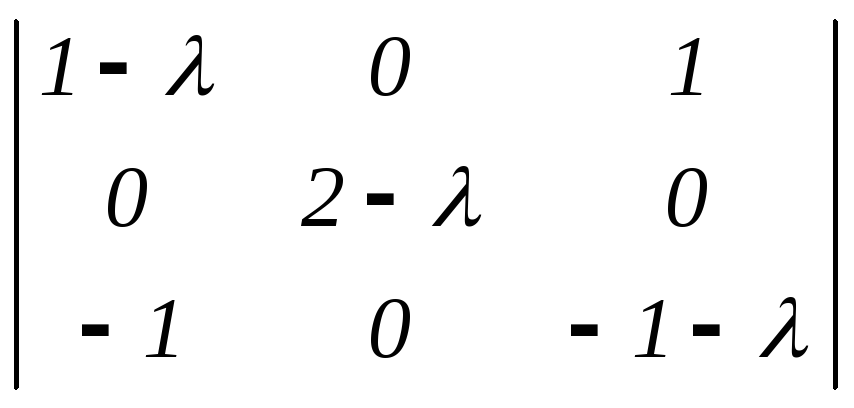= (1 –)(2 – )(–1 – ) + (2 – ) =

= (2 – )((1 – )(–1 – ) + 1) = (2 – )² = 0.

Таким образом, характеристическое уравнение для матрицы А имеет вид (2 – )² = 0.

II. Находим собственные числа матрицы А, решая характеристическое уравнение:

₁ = 2, _2,3 = 0. Таким образом, Sp() = Sp(A) = {2, 0}.

III. Находим собственные векторы матрицы А.

а) для ₁ = 2:

составляем однородную систему линейных уравнений и находим её общее решение методом Гаусса:

.

Таким образом, общее решение имеет вид 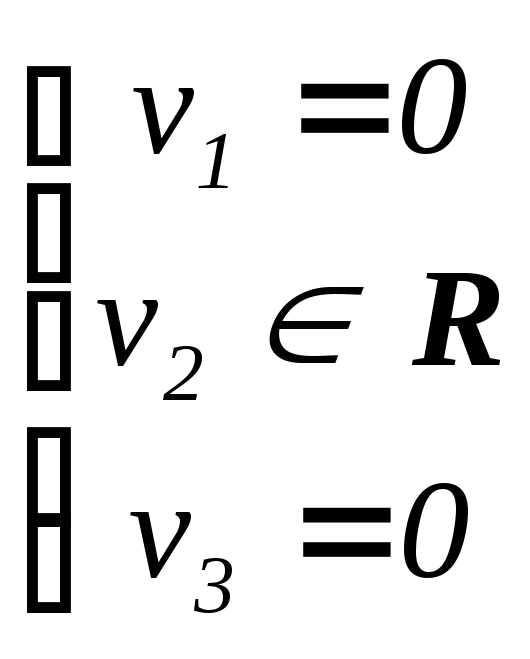, а векторы(v₂  0) являются собственными векторами матрицы А, соответствующими собственному числу ₁ = 2.

б) для _{2, 3} = 0:

составляем однородную систему линейных уравнений 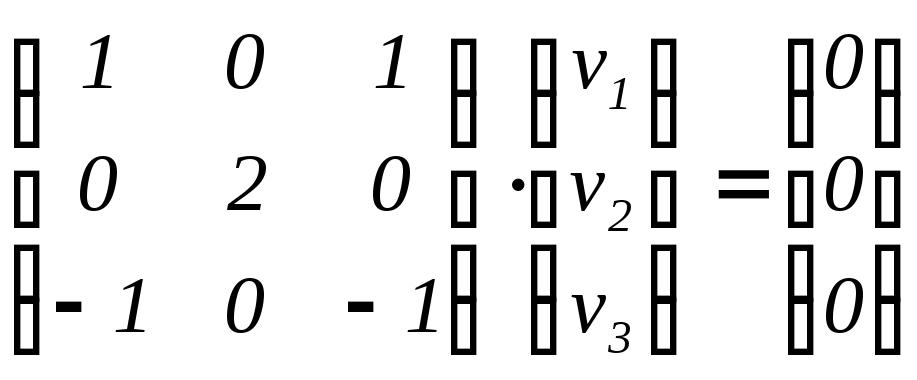и находим её общее решение 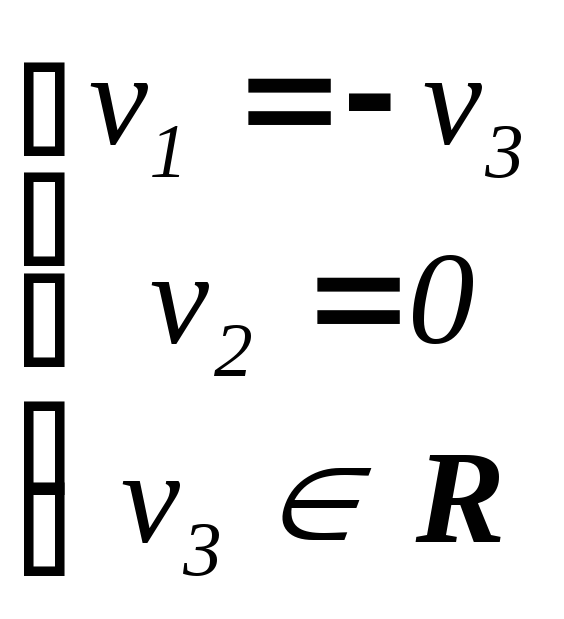(?!). Таким образом, векторы, гдеv₃  0, являются собственными векторами матрицы А, соответствующими собственному числу _{2 , 3} = 0.

IV. Находим собственные векторы исходного линейного оператора по формуле v = e[v]_e .

a) для ₁ = 2: v = (e₁ , e₂ , e₃) = v₂e₂ = v₂(0; 1; 0) = (0; v₂ ; 0) , где v₂  R \ {0}.

б) для _2,3 = 0:

v = (e₁ , e₂ , e₃) = –v₃e₁ + v₃e₃ = –v₃(1; 0; 0) + v₃(0; 0; 1) = (–v₃ ; 0; v₃ ), где v₃  R \ {0}.

Итак, линейный оператор  имеет собственные числа ₁ = 2 и _2,3 = 0. Первому из них отвечают собственные векторы (0; v₂ ; 0) , где v₂  R \ {0}, а двум другим – векторы (–v₃ ; 0; v₃ ), где v₃  R \ {0}.