Свойства скалярного произведения

1⁰. скалярное произведение аддитивно по второму аргументу:

 u, v, w  V (u , v + w) = (u , v) + (u , w).

Действительно, используя свойства симметричности и аддитивности по первому аргументу, имеем:

(u , v + w) = (v + w, u) = (v, u) + (w, u) = (u, v) + (u, w) .

2⁰. скалярное произведение однородно по второму аргументу:

 u, v  V    R (u, v) = (u, v).

Аналогично предыдущему, (u, v) = (v, u) = (u, v).

3⁰.  v  V (v, 0) = (0, v) = 0 .

В самом деле, по свойству 2⁰, (v, 0) = (v, 00) = 0(v, 0) = 0.

4⁰. скалярное произведение билинейно:  k, n  N  u₁ , … , u_n , v₁ , … , v_k  V

 ₁ , … , _n , ₁ , … , _k  R .

В самом деле, используя свойства аддитивности и однородности, имеем:

5⁰. Пусть V – конечномерное векторное пространство со скалярным произведением и базисом (e₁ , … , e_n ). Тогда скалярное произведение однозначно определяется значениями (e_i , e_j ) (1   n).

Если 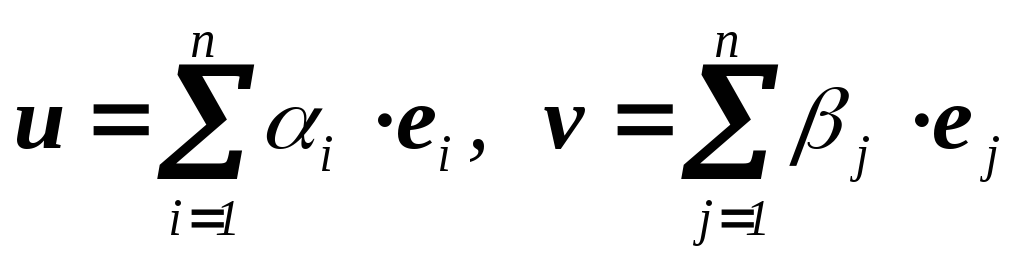, то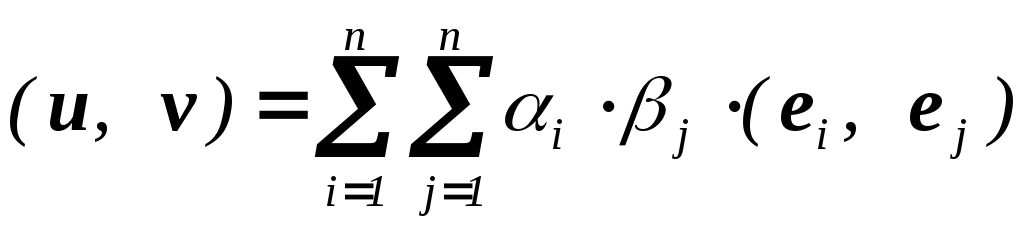. Таким образом, скалярное произведение векторов u, v  V полностью определяется их координатами _i ,  _j и указанными скалярными произведениями базисных векторов.

6⁰. Если V – конечномерное векторное пространство со скалярным произведением и базисом e = (e₁ , … , e_n), где (e_i , e_j) = 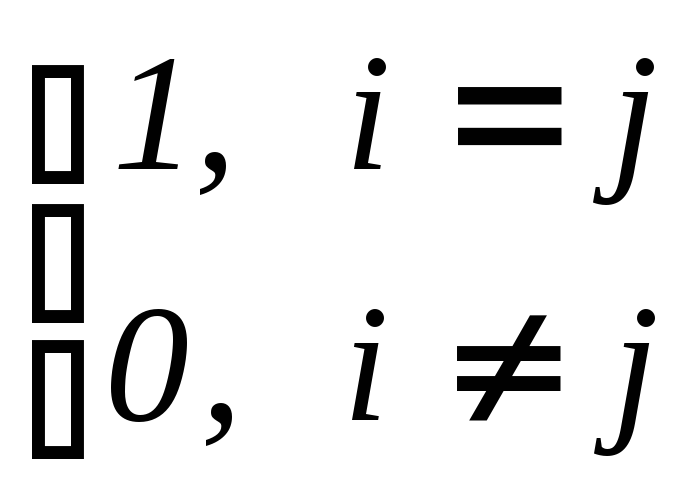, то u, v  V (u, v) = [u]_e[v]_e (напомним, что [x]_e – координатная строка вектора x  V в базисе e).

Если , то.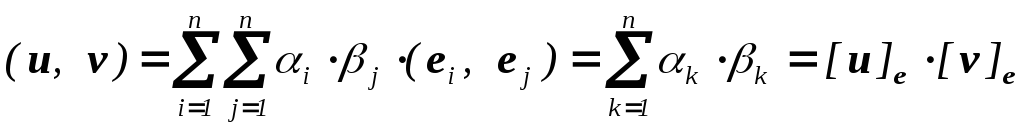

Любая упорядоченная пара (V, (_, _)), где V – векторное пространство, а (_, _) – скалярное произведение на V , называется евклидовым пространством. Необходимость такого формализма вызвана тем, что скалярное произведение на V можно задать по-разному. Поэтому, например,

(R², (u, v) = x₁y₁ + 2x₂y₂)  (R², (u, v) = x₁y₁ + x₂y₂).

Евклидово пространство (Rⁿ, (u, v) = x₁y₁ + … + x_ny_n) называется стандартным n-мерным евклидовым пространством, а скалярное произведение, заданное в нём – стандартным скалярным произведением в Rⁿ.

§ 2. Длины и углы в евклидовых пространствах

Пусть (V, (_, _)) – евклидово пространство. Для каждого v  V назовём длиной v (или его нормой) величину |v| = . Ввиду свойства неотрицательности скалярного произведения, длина любого вектора определена.

Свойства длины в евклидовых пространствах

1⁰.  v  V |v|  0,  v  V |v| = 0  v = 0.

Оба утверждения выполнены ввиду свойства неотрицательности и свойства 3⁰ скалярного произведения.

2⁰.  v  V    R |v| = |||v|.

Это верно ввиду однородности скалярного произведения (?!).

3⁰.  u, v  V |(u , v)|  |u||v| – неравенство Коши-Буняковского-Шварца.

Действительно, пусть t – произвольное действительное число. Тогда, по свойствам скалярного произведения имеем:

0  (u + tv, u + tv) = (u, u) + 2t(u, v) + t²(v, v).

Итак, полученный квадратный трёхчлен всюду неотрицателен. Поэтому его дискриминант неположителен: D = (2(u , v))² – 4(u, u)(v, v) 0,т.е. (u, v)²   (u, u)(v, v) = (|u||v|)² , что и требовалось.

4⁰.  u, v  V | u + v|  |u| + |v| – неравенство треугольника.

| u+v|  |u| + |v|  | u+v|²  (|u| + |v|)² 

 (u + v, u + v)  (u, u) + 2+ (v, v) 

 (u , u)+2(u , v)+(v, v)  (u , u) + 2 + (v , v) 

 (u , v)  .

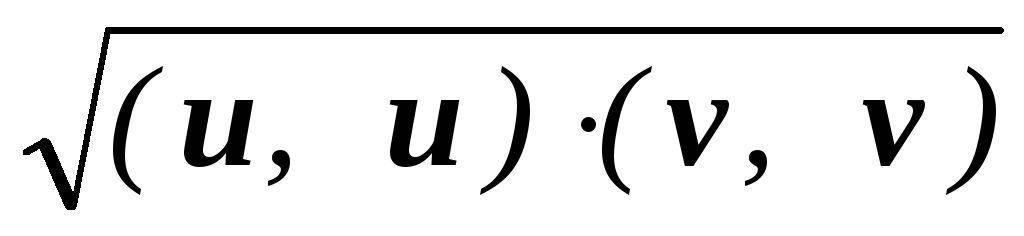Последнее неравенство следует из неравенства Коши-Буняковского. (А почему справедлива первая эквивалентность в этой цепочке ?!).

Итак, в евклидовых пространствах можно оперировать с длинами, как в обычной геометрии на плоскости. Оказывается эта аналогия идёт ещё дальше: в евклидовом пространстве можно ввести понятие угла между векторами. Именно, пусть u, v – два ненулевых вектора евклидова пространства V . По неравенству Коши-Буняковского, 0   1. Поэтому существует однозначно определённый угол   [0, ], косинус которого равен . Назовем его углом между ненулевыми векторами u и v из векторного пространства V.

Понятие угла позволяет доказывать для произвольного евклидова пространства аналоги обычных теорем плоской геометрии. Например, аналог теоремы косинусов выглядит так:

Теорема (косинусов для евклидовых пространств). Пусть a, b – произвольные ненулевые элементы евклидова пространства V (аналоги смежных сторон треугольника). Тогда |a – b|² = |a|² + | b|² – 2|a||b|cos , где  – угол между векторами a , b.

Доказательство. По свойствам скалярного произведения и определению длин и угла, имеем:

|a – b|² = (a – b, a – b) = (a , a) – 2(a , b) + (b , b) = |a|² + |b|² – 2|a||b|cos .

Теорема доказана.

Упражнение. докажите аналоги теоремы Пифагора и теоремы синусов.