§ 2. Матричный формализм в векторных пространствах

Пусть V – векторное пространство над полем F, n  N. Любой упорядоченный набор v = (v₁ , … , v_n)  Vⁿ, или аналогичный упорядоченный набор-столбец или даже множество v = {v₁ , … , v_n }  V будем называть конечной системой векторов в пространстве V или кратко к.с.в. В каком именно виде будут возникать в дальнейшем к.с.в. зависит от контекста: к.с.в. в виде множества удобно использовать, если не существенен порядок рассматриваемых векторов; если же порядок важен для рассуждений, то будем использовать к.с.в. в виде строк или столбцов (в зависимости от специфики конкретной ситуации).

Пример: Пусть (–1; 2; 3), (3; 1; 1)  R³. Тогда ((–1; 2; 3), (3; 1; 1))  (R³)²,  ²(R³) , {(–1; 2; 3), (3; 1; 1)}  R³ – конечные системы векторов.

Пусть v = {v₁ , … , v_n} – к.с.в. , ₁ , … , _n  F. Тогда линейную комбинацию векторов ₁v₁+…+_nv_n  V удобно записывать, используя матричные обозначения. Так, если v = (v₁ , … , v_n)  Vⁿ,  =  ⁿF, то можно естественным образом определить результат умножения v “строки” v на столбец  как v = (v₁ , … , v_n) = v₁₁+…+v_n_n = ₁v₁+…+_nv_n  V. Такая символика хорошо согласуется с обычными матричными обозначениями. В точности так же, если v =  ⁿV,  = (₁ ; … ; _n)  Fⁿ , то можно определить результат умножения v строки  на “столбец” v формулой v = (₁ ; … ; _n) = ₁v₁+…+_nv_n  V. Таким образом, линейная комбинация векторов является результатом умножения векторной “строки” на скалярный столбец или скалярной строки на векторный “столбец”.

Матричный формализм можно расширить далее, распространив его на матрицы. Пусть v = (v₁ , … , v_n)  Vⁿ, А  M(n, m, F). Тогда определим результат умножения к.с.в. v на матрицу A как к.с.в. vA = (u₁ , … , u_m)  V^m, где u_i = va⁽ⁱ⁾ = . Таким образом, каждый вектор к.с.в. u является результатом умножения строки v = (v₁ , … , v_n) на соответствующий столбец матрицы А . Аналогично определяется результат умножения матрицы A  M(m, n, F) на к.с.в. v = :Av =  ^mV, где компоненты u_i вычисляются естественно: u_i = a_iv = .

Кроме того, условимся складывать две к.с.в. одинакового “размера” по обычному правилу: если v = (v₁ , … , v_n), u = (u₁ , … , u_n)  Vⁿ , то полагаем v + u = (v₁ + u₁ , … , v_n + u_n). Аналогично определяется сложение к.с.в. в виде столбцов: если v = , u =  ⁿV, то v+u = .

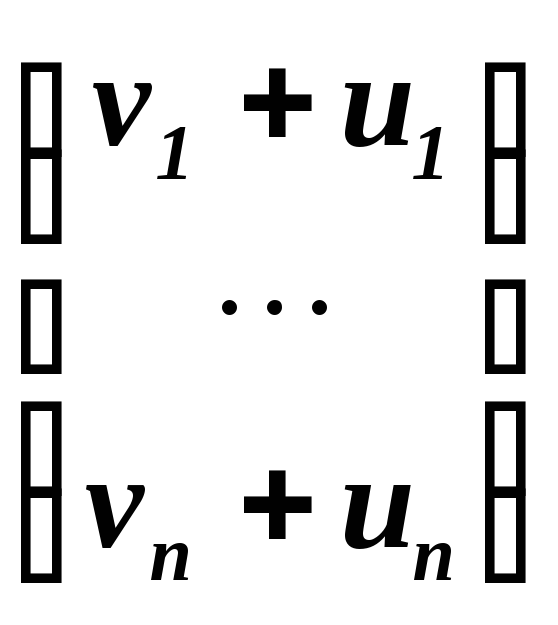Простейшие свойства матричного формализма

1⁰. Для любых к.с.в. u = (u₁ , … , u_n), v = (v₁ , … , v_n), w = (w₁ , … , w_n)  Vⁿ сложение ассоциативно: (u+v)+w = u+(v+w).

2⁰. Для любых к.с.в. u = (u₁ , … , u_n), v = (v₁ , … , v_n)  Vⁿ сложение коммутативно: u+v = v+u.

3⁰. Существует нулевая к.с.в. 0 = (0, … , 0)  Vⁿ со свойством нейтральности по сложению: для любой к.с.в v = (v₁ , … , v_n)  Vⁿ выполнено 0 + v = v = v + 0.

4⁰. Для любой к.с.в. v = (v₁ , … , v_n)  Vⁿ существует противоположная к.с.в. –v = (–v₁ , … , –v_n)  Vⁿ со свойством v + (–v) = 0 = (–v) + v.

5⁰. Для любой к.с.в. v = (v₁ , … , v_n)  Vⁿ и матриц А  M(n, k, F), B  M(k, m, F) справедлив аналог ассоциативности: (vA)B = v(AB).

6⁰. Для единичной матрицы I_n  M(n, F) и к.с.в. v = (v₁ , … , v_n)  Vⁿ выполнено равенство vI_n = v.

7⁰. Для любой к.с.в. v = (v₁ , … , v_n)  Vⁿ и матриц А, B  M(n, m, F) справедлив аналог дистрибутивности v(A + B) = vA + vB.

8 ⁰. Для любых к.с.в. u = (u₁ , … , u_n), v = (v₁ , … , v_n)  Vⁿ и матрицы А  M(n, m, F) выполнен аналог дистрибутивного закона: (u + v)A = = uA + vA.

Доказательства этих свойств полностью аналогичны соответствующим доказательствам правил действия со строками и матрицами. Например, свойство 5⁰ можно доказать так: если vA = u  V^k, uB = w  V^m, AB = C, vC = x, то

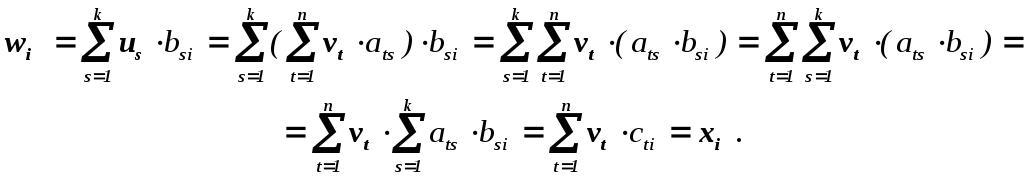
Отметим попутно, что первые четыре свойства означают, что множество Vⁿ всех n-элементных систем векторов является абелевой группой относительно введённой операции сложения к.с.в.

9⁰. Для любых к.с.в. u = (u₁ , … , u_n), v = (v₁ , … , v_n)  Vⁿ и обратимой матрицы А  GL(n, F) равенство u = vA равносильно v = uA^–1 .

Действительно, если u = vA, то uA^–1 = (vA)A^–1 = v(AA^–1) = vI_n = v. Точно так же из равенства v = uA^–1 выводится равенство u = vA (?!).

10⁰. Для любой к.с.в. v = (v₁ , … , v_n)  Vⁿ и матриц А, В  M(n, m, F) равенство vA = vB равносильно равенству v(A – B) = 0  Vⁿ.

В самом деле, vA = vB  ( j (1  j  m) va^(j) = vb^(j))  ( j (1  j  m) v(a^(j) – b^(j)) = 0  V)  v(A – B) = 0 = (0, … , 0) Vⁿ.

Упражнения: 1. Докажите все перечисленные выше и ещё недоказанные свойства.

2. Определите для каждого   F такую унарную операцию  умножения произвольной к.с.в. v = (v₁ , … , v_n)  Vⁿ на любой скаляр   F, чтобы алгебра (Vⁿ, + , { |   F}) была векторным пространством над полем F.

3. Сформулируйте и докажите аналогичные свойства к.с.в.-столбцов.

Следующие свойства используют матричный символизм для выражения некоторых фактов о линейно зависимых и линейно независимых системах векторов.

11⁰. Имеет место эквивалентность: (к.с.в. v = (v₁ , … , v_n)  Vⁿ линейно зависима)  (   ⁿF \ {0} v = 0).

12⁰. Имеет место эквивалентность: (к.с.в. v = (v₁ , … , v_n)  Vⁿ линейно независима)  (   ⁿF \ {0} v = 0   = 0)

Оба этих свойства являются переформулировками определений линейной зависимости и независимости на матричном языке.

13⁰. Имеет место эквивалентность: (к.с.в. v = (v₁ , … , v_n)  Vⁿ линейно независима)  ( A, B  M(n, m, F) vA = vB  A = B)

() Если v линейно независима и vA = vB, то v(A – B) = 0, т.е. (по 12⁰) все столбцы матрицы А – В нулевые, а значит А = В.

() следует из 12⁰ , если положить A =  , B = 0 .

14⁰. Имеет место эквивалентность: (e = (e₁ , … , e_n) – базис V)   ( f = (f₁ , … , f_m)  V^m  ! T  M(n, m, F) f = eT)

() Поскольку e – базис, каждый вектор f_i однозначно записывается в виде линейной комбинации векторов системы e: f_i = t_i1e₁ + … + t_ine_n . Если T = (t_ij) – матрица с компонентами t_ij (1  i  n, 1  j  m ), то f = eT. Такая матрица T определена однозначно: если f = eT = eS, то ввиду линейной независимости базиса e, свойство 13⁰ даёт T = S.

() Поскольку  v  V  t  ⁿF v = te (применили условие для системы f = (v)), то L(e) = V. Кроме того, система e линейно независима: если et = 0 для некоторого t  ⁿF, то et = 0 = e0 , и условие единственности матрицы T для к.с.в. f = {0} даёт t = 0 . Таким образом, e является базисом векторного пространства V.

15⁰. Пусть e = (e₁ , … , e_n) – базис векторного пространства V, f = eT, где T  M(m, n, F). Тогда ( f – базис V)  (T – обратимая матрица, т.е. T  GL(n, F))

() Если f = (f₁ , … , f_m) – базис, то n = m, т.к. базисы состоят из одного и того же числа векторов. Таким образом, T – квадратная матрица. Если она не обратима, то T – левый делитель нуля:  x  ⁿF \ {0} Tx = 0 , и fx = = eTx = e0 = 0, вопреки линейной независимости к.с.в. f .

() Во-первых, к.с.в. f линейно независима: если  x  ⁿF \ {0} fx = 0 , то eTx = 0 и ввиду линейной независимости базиса e получаем Tx = 0 , т.е. x = T ^–1Tx = T ^–10 = 0 – противоречие.

Во-вторых, L(f) = V : если v  V, то    ⁿF v = e , и значит, v = (eT)(T ^–1) = f( T ^–1) = f, где  = T ^–1 .