
- •Сборник
- •1. Содержание первого задания
- •1.1. Теоретические сведения к первому заданию
- •1.2. Пример выполнения первого задания
- •2. Содержание второго задания
- •2.1. Теоретические сведения ко второму заданию
- •2.2. Пример выполнения второго задания
- •3. Контрольные вопросы для самопроверки при подготовке к защите расчетно-графической работы
- •Список рекомендуемой литературы
- •Оглавление
2.2. Пример выполнения второго задания
Пример.
Механическая система, состоящая из
четырех тел (рис.2.6): грузов 1 и 4, блока 2
и катка 3, кинематически связанных между
собой нерастяжимыми нитями, приходит
в движение под действием сил тяжести
из состояния покоя. Учитывая трение
скольжения тела 4, трение качения тела
3, пренебрегая другими силами сопротивления
и массами нитей, определить:
1. Скорость тела 1 в тот момент времени, когда пройденный им путь станет равным S1.
2. Ускорения тел, движущихся поступательно, и ускорения центров масс тел, совершающих плоскопараллельное движение, угловые ускорения тел, совершающих вращательное и плоскопараллельное движения.
3. Реакции внешних и внутренних связей системы.
4.
Выбрав в качестве обобщенной координаты
пройденный телом 1 путь S
и составив уравнение Лагранжа второго
рода, найти зависимости
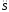 =f1(t),
=f1(t),
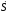 =
f2(t)
и
S
=
f3(t).
Полученные зависимости изобразить
графически в пределах движения заданной
системы 0<S<1,2.
=
f2(t)
и
S
=
f3(t).
Полученные зависимости изобразить
графически в пределах движения заданной
системы 0<S<1,2.
Необходимые
для расчета данные следующие: R2
=
R3
= R;
r3
= r,
m1
= 3m;
m2
= 2m;
m3
= m4
= m;
i3x
=
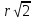 ;f
= 0,1; δ
= 0,001м; R/r
= 1,5; m
= 5 кг, r
= 0,25 м; S1
=1,2 м (здесь
m1
,
m2
,
m3
,
m4
- массы соответственно тел 1,2,3 и 4; i3
–
радиус инерции тела 3 относительно оси,
проходящей через его центр масс
перпендикулярно плоскости движения; f
– коэффициент трения скольжения; δ
–
коэффициент трения качения тела 3).
;f
= 0,1; δ
= 0,001м; R/r
= 1,5; m
= 5 кг, r
= 0,25 м; S1
=1,2 м (здесь
m1
,
m2
,
m3
,
m4
- массы соответственно тел 1,2,3 и 4; i3
–
радиус инерции тела 3 относительно оси,
проходящей через его центр масс
перпендикулярно плоскости движения; f
– коэффициент трения скольжения; δ
–
коэффициент трения качения тела 3).
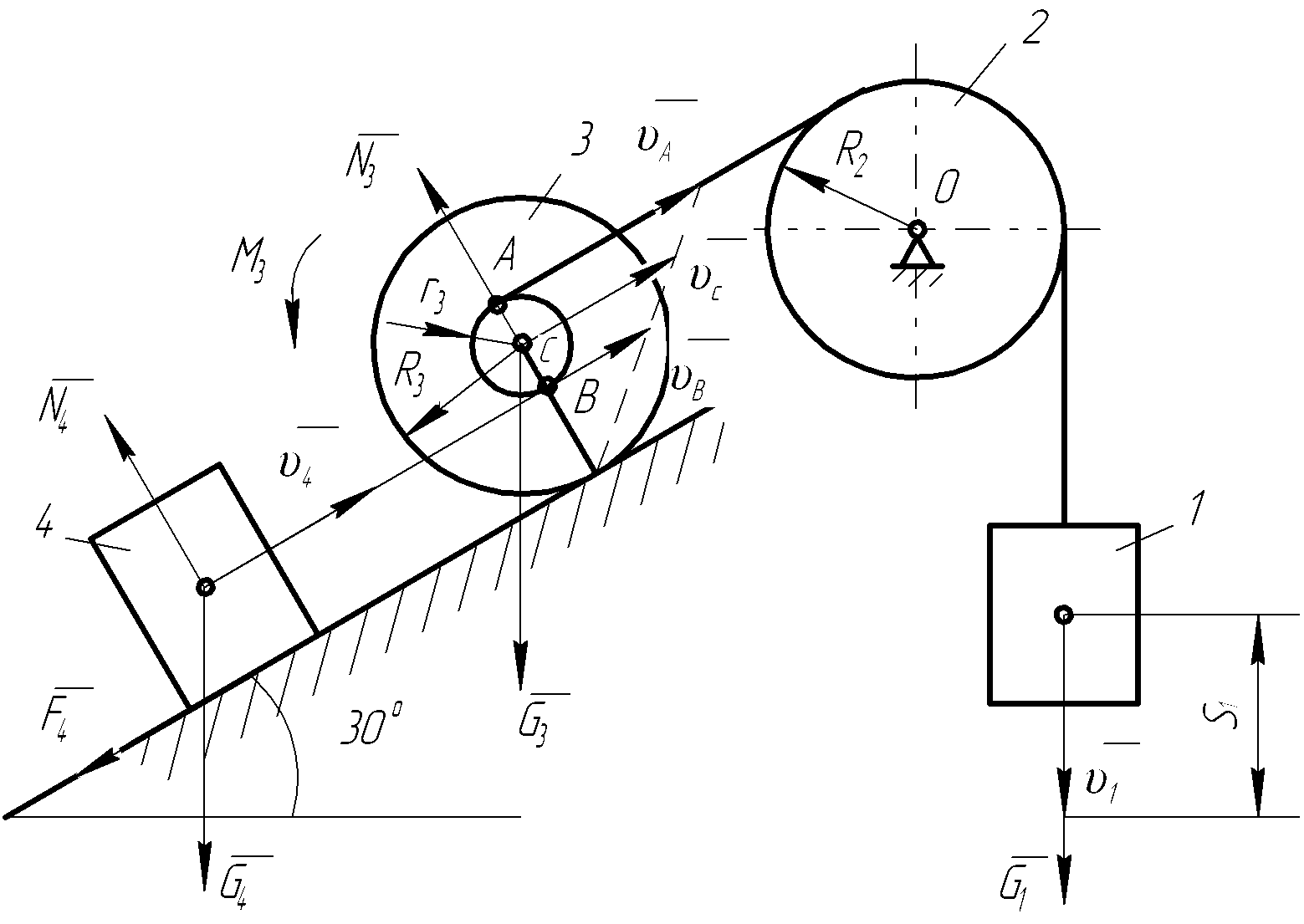
Рисунок 2.6 – Схема механической системы к выполнению второго задания
Решение
При
определении скорости тела 1 в момент
времени, когда пройденный им путь S1
будет
равным 1,2 м, воспользуемся теоремой об
изменении кинетической энергии (2.1). Так
как в начальный момент времени механическая
система находилась в покое, то Т0=0.
По условию задания соединяющие тела
системы нити предполагаются нерастяжимыми,
проскальзывание между телами отсутствует,
поэтому
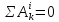 .
Тогда
выражение (2.1) примет упрощенный вид:
.
Тогда
выражение (2.1) примет упрощенный вид:
(2.18)
 .
.
Вычислим кинетическую энергию Т системы, когда груз 1 пройдет путь, равный 1,2 м. Груз 1 совершает поступательное движение, значит
Т1
=
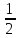 m1
m1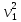 =
=
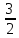
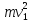 .
.
(2.19)
Блок 2 вращается вокруг неподвижной оси, поэтому
Т2
=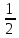 J2
J2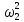 .
.
Момент инерции J2 блока 2 не задан, поэтому определяем его как для сплошного цилиндра по формуле:
(2.20)
J2
=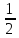 m2
m2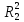 =2,25
mr2,
=2,25
mr2,
а угловую скорость находим из равенства:
𝜔2
=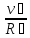 =
= .
.
(2.21)
Таким образом, кинетическая энергия блока 2 примет вид:
(2.22)
Т2
=
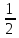 m
m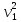 .
.
Так как каток 3 совершает плоскопараллельное движение, то
(2.23)
Т3
=
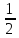 m
m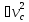 +
+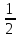 J2
J2
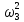 .
.
Поскольку
соединительные нити предполагаются
нерастяжимыми, скорость точки А
катка
3
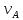 =
=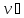 .
Точкар
является
мгновенным центром скоростей третьего
тела, значит
.
Точкар
является
мгновенным центром скоростей третьего
тела, значит
𝜔3=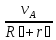 =
=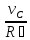 =
=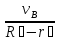 .
.
(2.24)
Из выражения (2.24) следует, что
(2.25)
𝜔3
=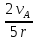 =
=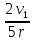 ,
,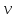 с=
с=
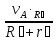 =
=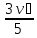 .
.
Момент инерции катка 3 определится по заданному радиусу инерции i3 по формуле:
(2.26)
Jс
= m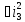 =
2mr2.
=
2mr2.
Тогда, подставляя (2.25) и (2.26) в (2.23), получим:
(2.27)
Т3
=
0,34m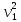 .
.
Кинетическая энергия груза 4
(2.28)
Т4
=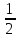 m4
m4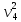 .
.
Из выражения (2.24) вытекает, что
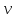 4
=
4
=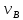 =
=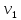
 =
0,2
=
0,2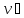 .
.
.
.
(2.29)
Тогда из (2.28) с учетом (2.29) следует, что
(2.30)
Т4
= 0,02m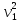 .
.
Теперь, складывая равенства (2.19), (2.22), (2.27) и (2.30), найдем кинетическую энергию всей системы:
(2.31)
Т
= Т1+
Т2+
Т3+
Т4
= 2,36m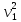 .
.
Найдем сумму работ всех внешних сил, приложенных к системе, на заданном ее перемещении. Для этого покажем на схеме все приложенные к системе внешние силы (см. рисунок 2.6). Работу силы тяжести G1 груза 1 найдем по формуле (2.5):
(2.32)
AG₁ = G1S1 = m1gS1=3mgS1.
Аналогично определяется работа силы тяжести катка 3:
(2.33)
AG₃ =- m3ghc=-mgScsin30°
(здесь hc- смещение центра масс С катка по вертикали в заданном перемещении системы, Sc – путь, пройденный точкой С при этом смещении).
Путь,
пройденный точкой С,
можно определить из выражения (2.25),
представив =3
=3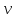 1/5
в виде
1/5
в виде
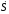 с=0,6
с=0,6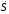 1.
Интегрируя это равенство, получим:
1.
Интегрируя это равенство, получим:
Sc = 0,6S1.
Тогда окончательно получим:
(2.34)
AG₃ = -0,3mgS1.
Аналогичным образом из выражения (2.25) несложно получить, что
(2.35)
𝜑3
=
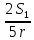 .
.
Работа сил сопротивления качению катка 3 определяется по формуле (2.7). В данном примере
(2.36)
Mc
= δN3
= δm3gcos30°
= 0,5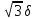 mg.
mg.
Тогда с учетом выражений (2.35) и (2.36) получим:
AM₃
=
-0,2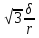 mgS1.
mgS1.
(2.37)
Работа силы тяжести груза 4
AG4 =-m4gS4·sin30° = - 0,1 mgS1.
(2.38)
где S4=0,2S1 (путь, пройденный телом 4, найдено из выражения (2.29) путем интегрирования).
Работу силы трения скольжения груза 4 определяем по формуле (2.6):
АF4
=- fN4S4
= -fm4gcos30°∙
0,2S1
= -0,1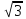 fmgS1.
fmgS1.
(2.39)
Наконец, складывая равенства (2.32), (2.34), (2.37), (2.38) и (2.39), получим:
∑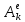 =
(2,6-0,1
=
(2,6-0,1 f
–
0,2
f
–
0,2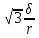 )mgS1.
)mgS1.
(2.40)
Подставляя выражения (2.31) и (2.40) в (2.18), после преобразований имеем:
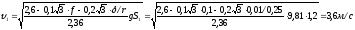
Далее, применяя общее уравнение динамики (2.8), найдем ускорения тел, движущихся поступательно и ускорения центров масс тел, совершающих плоскопараллельное движение, угловые ускорения тел, совершающих вращательное и плоскопараллельное движения.
В соответствии с этим уравнением изобразим на схеме системы активные силы и силы инерции (рисунок 2.7).
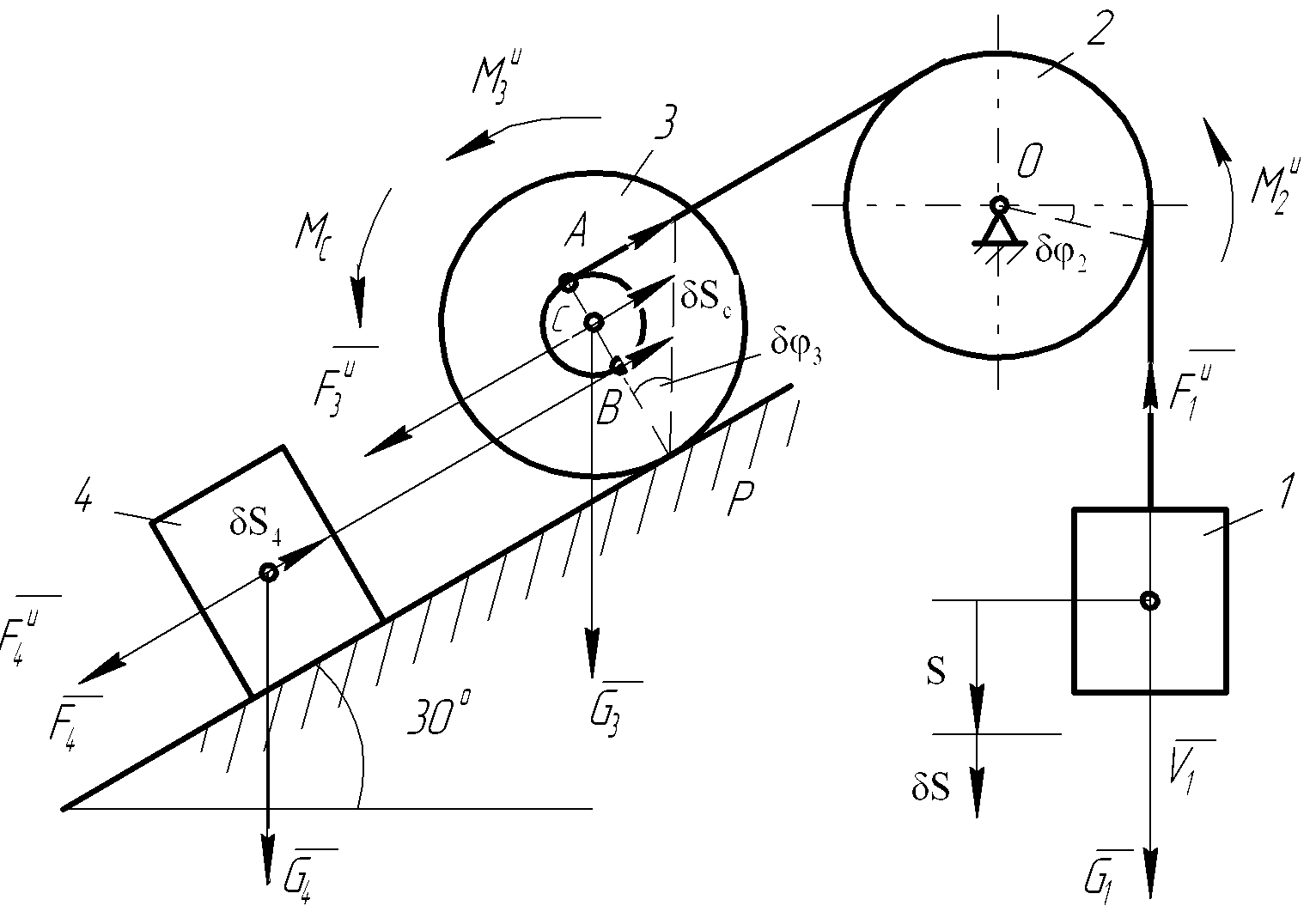
Рисунок 2.7 – Схема механической системы к выполнению п.2 задания 2
Так как тело 1 совершает поступательное движение, элементарные силы инерции всех точек его приводятся в соответствии с выражением (2.9) к равнодействующей, равной по модулю
(2.41)
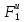 =
m1a1
=
3ma1,
=
m1a1
=
3ma1,
линия действия которой проходит через центр масс этого тела.
Блок
2 вращается вокруг неподвижной оси,
поэтому силы инерции точек этого тела
приводятся согласно выражению (2.10) к
паре сил с моментом, абсолютная величина
которого
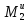 =J2ℇ2.
Здесь момент инерции Jх
определяется
равенством (2.20), а угловое ускорение ℇ2
находится из (2.21) дифференцированием
по времени:
=J2ℇ2.
Здесь момент инерции Jх
определяется
равенством (2.20), а угловое ускорение ℇ2
находится из (2.21) дифференцированием
по времени:
ℇ2=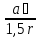 .
.
Тогда
(2.42)
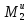 =
1,5ma1r.
=
1,5ma1r.
Согласно
выражений (2.11) и (2.12) элементарные силы
инерции катка 3 приводятся в его центре
масс к силе
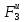 =m3aс
и паре сил с моментом, равным по абсолютной
величине
=m3aс
и паре сил с моментом, равным по абсолютной
величине
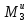 =Jсℇ3.
Момент инерции Jс
найден
раньше в выражении (2.26), а ускорение aс
и угловое ускорение ℇ3
определяются
из (2.25) дифференцированием по времени:
=Jсℇ3.
Момент инерции Jс
найден
раньше в выражении (2.26), а ускорение aс
и угловое ускорение ℇ3
определяются
из (2.25) дифференцированием по времени:
ℇ3
=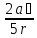 ,
aс
=
,
aс
=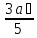 .
.
Отсюда
(2.43)
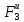 =
0,6ma1,
=
0,6ma1,
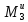 =
0,8ma1r.
=
0,8ma1r.
Тело 4 движется поступательно, значит
(2.44)
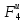 =
m4a4
= 0,2ma1,
=
m4a4
= 0,2ma1,
где a4=0,2a1(находится из (2.29) дифференцированием по времени).
Теперь дадим системе возможное перемещение и составим общее уравнение динамики согласно выражению (2.16):
G1δS1-
G3δScsin30°-
G4δS4
sin30°-F4δS4-Mcδ𝜑3-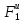 δS1-
δS1-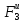 δSc-
δSc-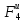 δS4-
δS4-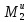 δ𝜑2-
-
δ𝜑2-
- δ𝜑3=0.
δ𝜑3=0.
(2.45)
Так как наложенные на механическую систему связи являются стационарными, удерживающими и голономными, все возможные перемещения системы выражаются через возможное перемещение δS1 соответственно:
δ𝜑2
=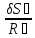 =
= ,
δ𝜑3
=
,
δ𝜑3
=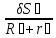 =0,4
=0,4
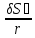 ,δSc
= δS1
,δSc
= δS1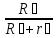 = 0,6δS1,
= 0,6δS1,
(2.46)
δS4
=
δS1
=
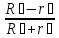 =0,2δS1.
=0,2δS1.
Подставляя
в выражение (2.45) найденные ранее момент
силы трения качения (2.36), силу трения
скольжения F4=fm4qcos30°=0,5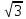 fmg,
а также выражения возможных перемещений
(2.46), получим:
fmg,
а также выражения возможных перемещений
(2.46), получим:
(2.47)
(2,6-0,1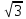 f
-0,2
f
-0,2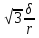 )g-
4,72a1
= 0 .
)g-
4,72a1
= 0 .
Откуда
a1
=
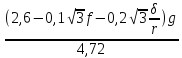 =
=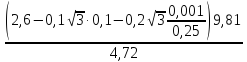 =
5,365 м/с2.
=
5,365 м/с2.
Теперь, используя полученные выше зависимости, находим:
ac = 0,6a1 = 0,6∙5,365 = 3,219 м/с2,
a4 = 0,2a1 = 0,2∙5,365 = 1,073 м/с2,
ℇ2
=
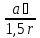 =
= =
14,307
1/с2,
=
14,307
1/с2,
ℇ3
= 0,4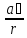 =
0,4
=
0,4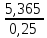 =
8,584
1/с2.
=
8,584
1/с2.
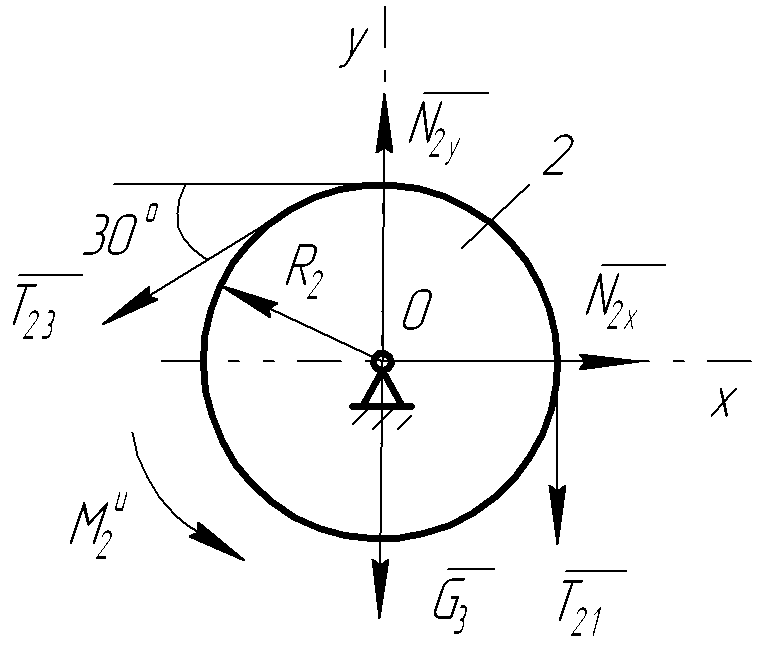
Для выполнения пункта 3 задания изобразим по отдельности тела механической системы (рисунок 2.8), приложив к ним силы тяжести, реакции внешних и внутренних связей и силы инерции.
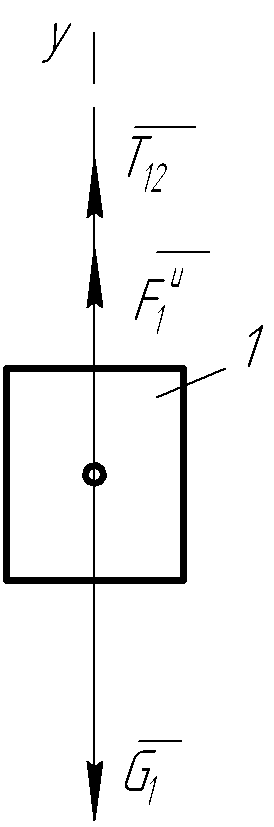
В соответствии с принципом Даламбера, система сил, приложенных к телу 1 (рисунок 2.8, а), находится в равновесии, подтверждаемом уравнением:
(2.48)
 Fky
= T12
+
Fky
= T12
+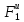 -
G1
= 0.
-
G1
= 0.
Отсюда с учетом G1=m1g=3 mg и равенства (2.41)
T12
=
G1
-
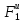 =
3m(g-a1)
=3∙5(9,81-5,365)
= 66,675 H.
=
3m(g-a1)
=3∙5(9,81-5,365)
= 66,675 H.
|
а |
б |
|
|
|
|
в |
г |
Рисунок 2.8 – Схема сил в механической системе к выполнению п.3 задания 2
Составим уравнения равновесия системы сил, приложенных к блоку 2(рис.2.8, б) в виде:
(2.49)
 Fkx
= N2x-T23
cos30°
= 0,
Fkx
= N2x-T23
cos30°
= 0,
(2.50)
 Fky
=
Fky
=
 N2y-
T23sin30°-
G2-
T21
= 0,
N2y-
T23sin30°-
G2-
T21
= 0,
 m0(
m0(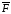 k)
= T23R2-
T21R2+
k)
= T23R2-
T21R2+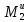 =
0.
=
0.
(2.51)
Из
(2.51), учитывая, что T21=T12,
а момент
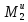 найден в (2.42), следует
найден в (2.42), следует
T23
= T32
= T12-
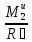 =
T12-
ma1
= 66,675-5∙5,365
= 39,852 Н.
=
T12-
ma1
= 66,675-5∙5,365
= 39,852 Н.
Тогда из (2.49) и (2.50) следует:
N2x=T23 cos30°=39,852∙cos30°=34,128 Н,
N2y = T23sin30°+G2+T12 = 39,852∙0,5+98,1+66,675 = 184,701 Н.
Следовательно
N2=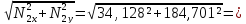 187,827
Н.
187,827
Н.
Составим уравнения равновесия для системы сил, приложенных к катку 3 (рисунок 2.8, в):
(2.52)
 Fkx'
=
F3+
T32-
Fkx'
=
F3+
T32-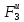 -
T34-
G3
sin30°
= 0,
-
T34-
G3
sin30°
= 0,
(2.53)
 Fky'
=
N3-
G3
cos30°
= 0,
Fky'
=
N3-
G3
cos30°
= 0,
(2.54)
 mp(
mp( k)=
k)=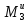 +Mc+
T34(R3-r3)+
+Mc+
T34(R3-r3)+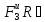 +G3
+G3 +
sin30°-T32(R3+r3)=
0.
+
sin30°-T32(R3+r3)=
0.
Из (2.54) с учетом полученных ранее результатов следует:
T34=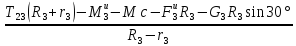 =
=
=
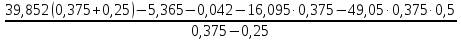 =
34,129
Н
,
=
34,129
Н
,
где R3 = R= 1,5r = 1,5∙0,25 = 0,375м;
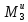 =
0,8ma1r
=
0,8∙5∙5,365∙0,25
= 5,365 Нм;
=
0,8ma1r
=
0,8∙5∙5,365∙0,25
= 5,365 Нм;
 =
0,5
=
0,5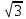 ∙δmg
= 0,5
∙δmg
= 0,5 ∙0,001∙5∙9,81
= 0,042 Нм;
∙0,001∙5∙9,81
= 0,042 Нм;
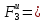 0,6ma1
=
0,6∙5∙5,365
= 16,095 Н;
0,6ma1
=
0,6∙5∙5,365
= 16,095 Н;
G3 = m3g = mg = 5∙ 9,81 = 49,05 H.
Теперь из (2.52) можно определить силу трения скольжения:
F3
=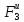 +T34+G3
sin30°-Т23
= 16,095+34,129+49,06∙0,5-39,852=60,014
Н, а из
(2.53)
+T34+G3
sin30°-Т23
= 16,095+34,129+49,06∙0,5-39,852=60,014
Н, а из
(2.53)
N3 = G3 cos30° = 49,05∙0,866 = 42,5 Н.
Заметим, соотношение (2.52) было использовано ранее при определении момента сил трения качения М3.
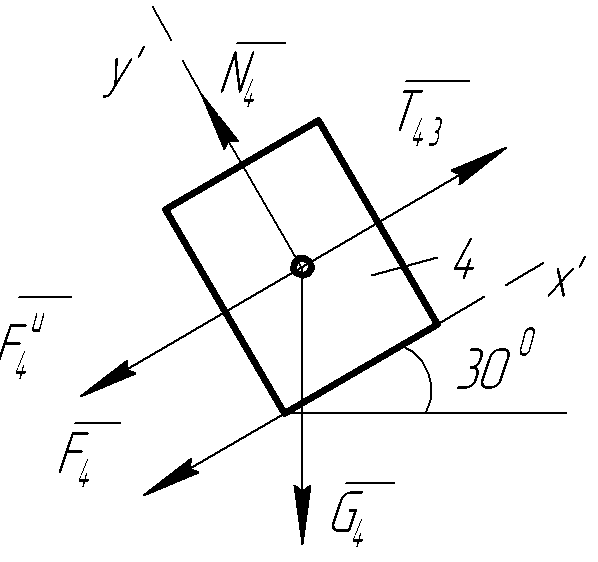
Уравнения равновесия системы сил, приложенных к грузу 4:
 Fkx'
=
Т43-
Fkx'
=
Т43-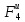 -
F4-G4sin30°=0,
-
F4-G4sin30°=0,
(2.55)
 Fky'
=
N4-
G4
cos30°=0.
Fky'
=
N4-
G4
cos30°=0.
(2.56)
В уравнении (2.55) все величины уже известны, поэтому оно может служить для проверки проведенных расчетов. Подставляя в него найденные ранее величины, получим:
34,129-5,4-4,2-5∙9,81∙0,5≈0.
Заметим, равенство (2.56) уже было использовано ранее при определении работы сил трения скольжения A F4.
Наконец, приступим к выполнению пункта 4 задания. Выберем в качестве обобщенной координаты пройденный телом 1 путь S (рисунок 2.7), то есть S=q. Тогда уравнение Лагранжа второго рода будет иметь вид (2.17).
Кинетическая
энергия системы была определена в п.1
выражением (2.31). Выразив в нем
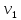 через
через
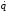 ,получим:
,получим:
(2.57)
T=2,36m2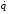 2.
2.
Для определения обобщенной силы сообщаем системе возможное перемещение и вычислим на этом перемещении сумму работ всех действующих внешних сил в виде:
(2.58)
 δАк=G1∙δS1
–
G3δSc
sin30°-Mc∙δ𝜑3-G4δS1∙sin30°-
F4δS4.
δАк=G1∙δS1
–
G3δSc
sin30°-Mc∙δ𝜑3-G4δS1∙sin30°-
F4δS4.
Заметим, здесь силы инерции и моменты сил инерции не отражены, так как обобщенные силы инерции уже выражены через кинетическую энергию системы в уравнении Лагранжа второго рода.
С учетом выражений (2.46), выделив в выражении (2.58) коэффициент при δS1, получим:
Q= G1-0,6G3 sin30°-0,4 M3/r-0,2G4 sin30°-0,2F.
Откуда с учетом полученных выше результатов и исходных данных имеем:
(2.59)
Q=2,6mg.
Теперь, подставив (2.57) и (2.59) в выражение (2.17) получим:
(2.60)
4,72m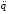 =2,6mg.
=2,6mg.
Далее,
интегрируя выражение (2.60) по времени t
с учетом начальных условий
 0=0,
S0=0,
получим:
0=0,
S0=0,
получим:
(2.61)
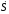 =0,55gt,
=0,55gt,
(2.62)
S=0,275gt2 .
Приняв в выражении (2.62) S= S1=1,2 м, находим время движения системы t=0,67 с.
В
соответствии с зависимостями (2.60), (2.61)
и (2.62) формируем массивы данных для
построения графиков
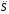 =f1(t),
=f1(t),
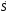 =
f2(t)
и S=f3(t)
(таблица 2.3).
=
f2(t)
и S=f3(t)
(таблица 2.3).
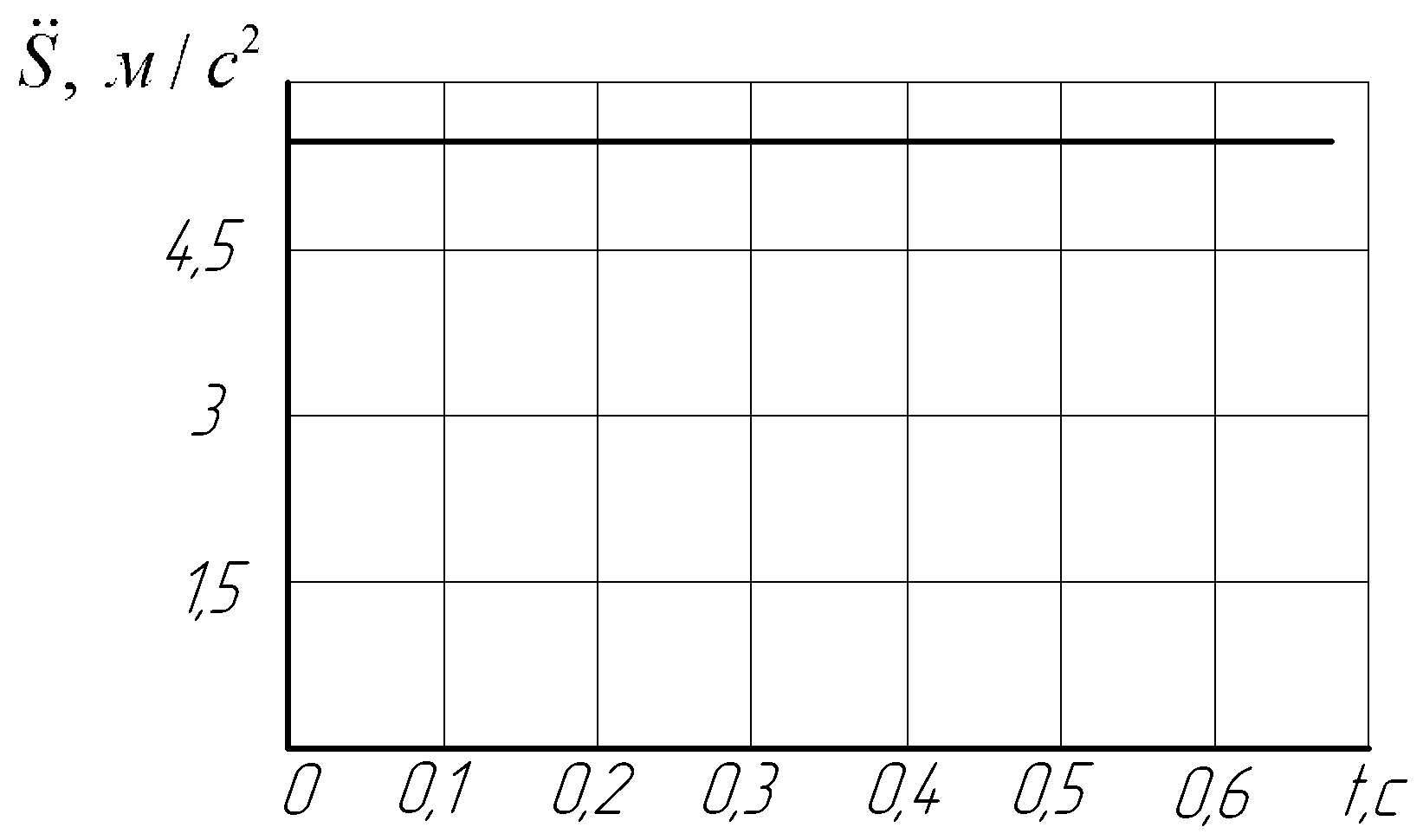
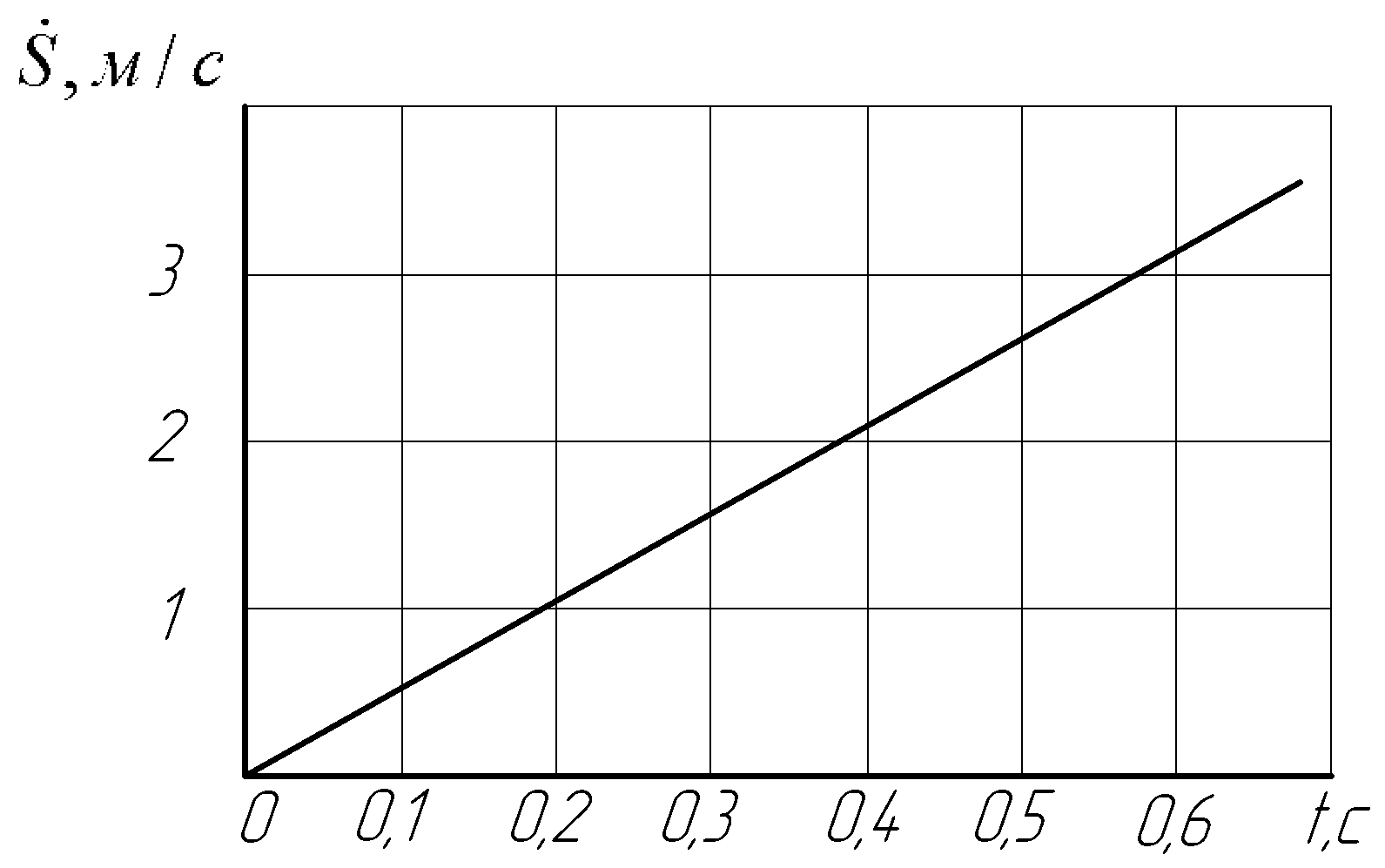
Таблица 2.3 – Массив данных для построения графиков движения системы
|
Время t,c |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,67 |
|
Ускорение
|
5,39 |
5,39 |
5,39 |
5,39 |
5,39 |
5,39 |
5,39 |
5,39 |
|
Скорость
|
0 |
0,539 |
1,078 |
1,617 |
2,156 |
2,695 |
3,234 |
3,611 |
|
Перемещение S, м |
0 |
0,027 |
0,108 |
0,242 |
0,431 |
0,674 |
0,970 |
1,200 |
На
рисунке 2.9 показаны построенные по этому
массиву графики
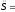 =f1(t),
=f1(t),
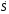 =
f2(t)
и S=f3(t).
=
f2(t)
и S=f3(t).
S,м
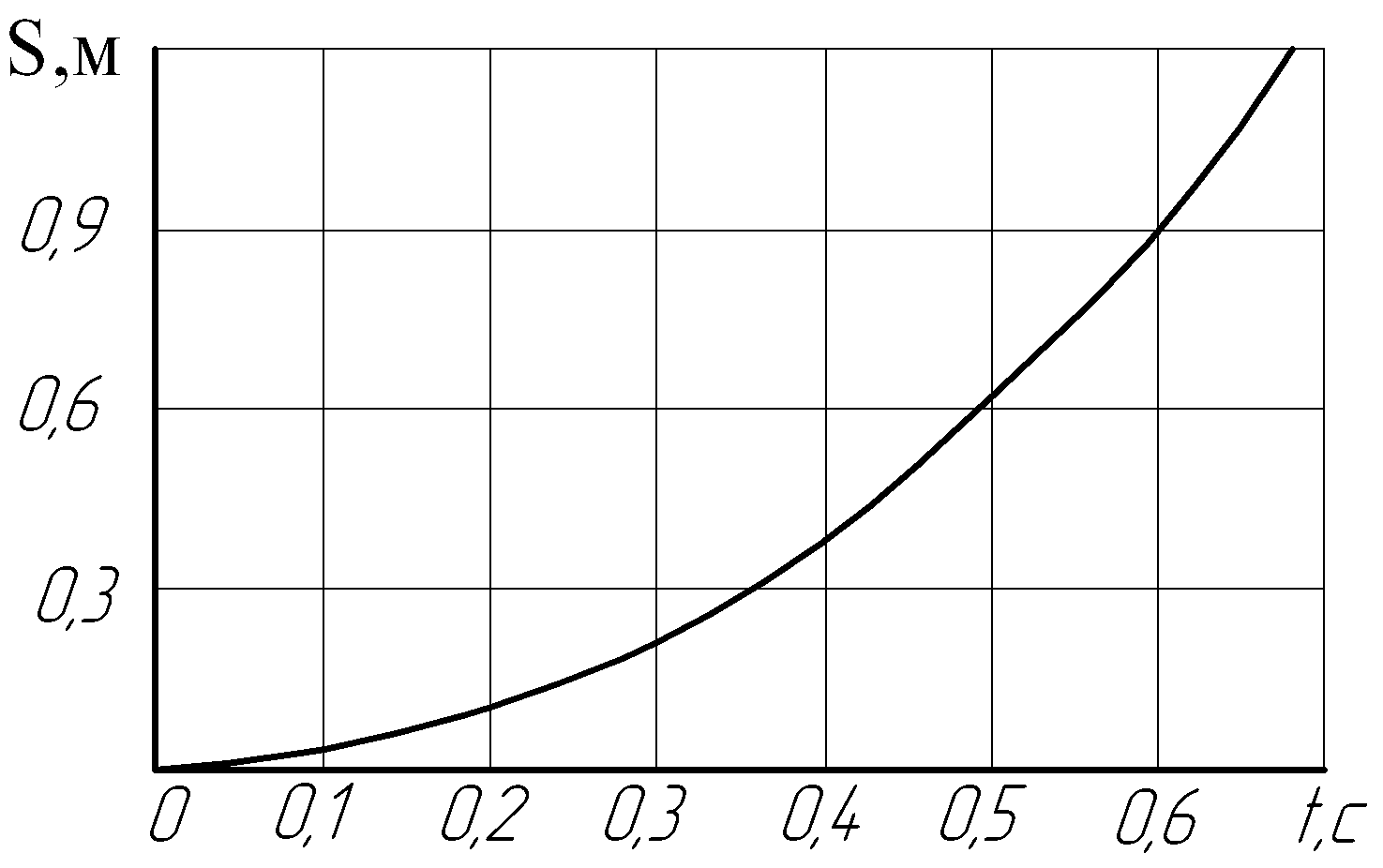
Рисунок
2.9 – Графики движения
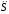 =f1(t),
=f1(t),
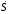 =
f2(t)
и S=f3(t)
исследуемой механической системы
=
f2(t)
и S=f3(t)
исследуемой механической системы


 ,
м/с2
,
м/с2 ,
м/с
,
м/с