- •Міністерство освіти і науки України
- •Основи статистичної обробки результатів вимірювання фізичних величин
- •Похибки непрямих вимірювань
- •Остаточний запис результату вимірювання
- •Графічне представлення результатів вимірювань.
- •Рекомендації щодо оформлення звіту до лабораторної роботи
- •Методи перевірки гіпотез про закони розподілу випадкових величин
- •Перевірка нормальності розподілу за допомогою показників асиметрії і ексцесу
Рекомендації щодо оформлення звіту до лабораторної роботи
Звіт з лабораторної роботи повинен включати :
1. Назву роботи.
2. Мету роботи.
3. Перелік приладів і матеріалів.
4. Схему експериментальної установки.
5. Короткі теоретичні відомості та робочу формулу.
6. Експериментальні результати із зазначенням одиниць вимірювання й похибки приладу. Запис параметрів установки, необхідних для подальших розрахунків (також із зазначенням одиниць і похибок).
7. Оброблені результати вимірювань, представлені у вигляді таблиць, чисел, графіків – відповідно до завдання, визначеного в методичній розробці до лабораторної роботи.
8. Обчислення похибок.
9. Аналіз результатів: порівняння з табличними даними, з теорією, з даними інших експериментів – також з урахуванням похибок.
10. Висновки.
Додаток №2.
Схема обчислення похибок для прямих вимірювань
1.
Обчислюється середньоарифметичне
значення серії з n
вимірювань:
![]() .
.
2.
Знаходяться похибки окремих вимірювань:
![]() .
.
3.
Обчислюються квадрати похибок окремих
вимірювань
![]() .
.
4.Якщо одне з вимірювань різко відрізняється за своїм значенням від решти вимірювань, то слід перевірити чи не є воно промахом.
5.
Визначається середньоквадратична
похибка середнього значення прямих
вимірювань:
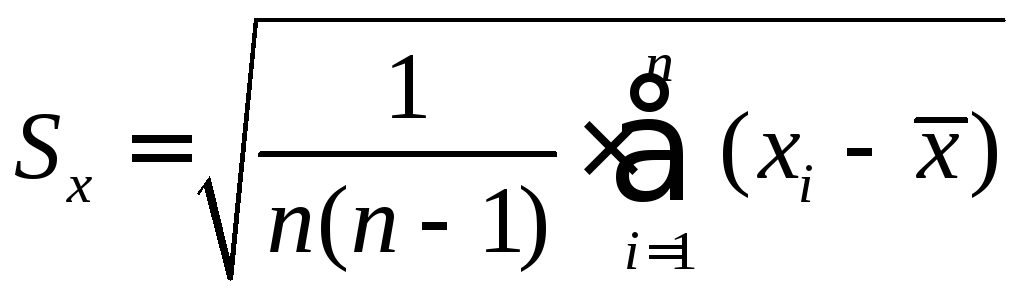 .
.
6.
Задають значення коефіцієнта надійності
=0.95.
За допомогою відповідних таблиць для
даного значення величини
![]() і nвизначають
величину
коефіцієнта Стьюдента
і nвизначають
величину
коефіцієнта Стьюдента
![]() .
Знаходять похибку вимірювань
.
Знаходять похибку вимірювань![]() ,
яка визначається межею довірчого
інтервалу:
,
яка визначається межею довірчого
інтервалу:![]() .
.
7.Якщо величина похибки вимірювань, визначена в п.6, виявиться порівнянною з величиною похибки приладу, то
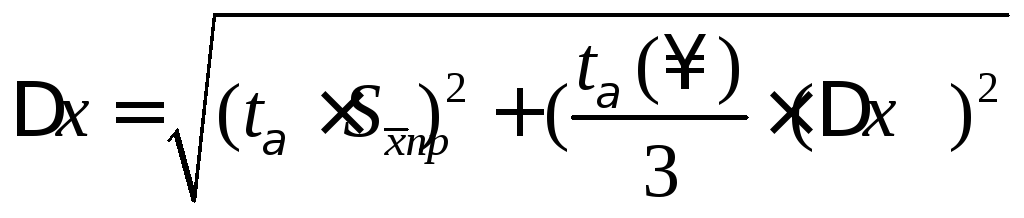
Для
=0.95
![]() =1.96.
=1.96.
8.Обчислюється
відносна
похибка
![]() :
:
9. Остаточний результат записується у вигляді:
![]() ,
,
![]() (%).
(%).
Додаток №3 Схема обчислення похибок для непрямих вимірювань
1.Для кожної серії вимірювань проводитися обробка, як описана у додатку №2. При цьому для всіх вимірюваних величин задають одне і те ж значення надійності.
2.
Обчислюється середнє значення шуканої
величини:
![]() .
.
3. Обчилюються часткові похідні:
![]() ,
,
![]() ,
,![]()
4.Обчислюється похибка непрямих вимірювань:
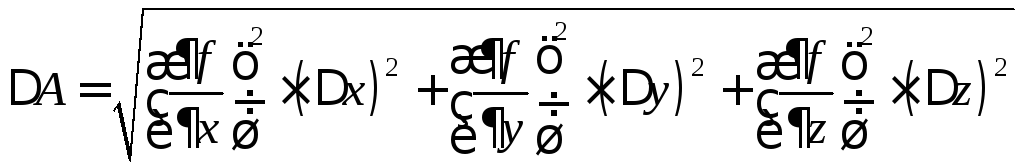 .
.
5.Остаточний результат записується у вигляді:
![]()
![]() ,%
,%
де
![]() –
відносна похибка непрямих вимірювань.
–
відносна похибка непрямих вимірювань.
Додаток №3.
Закони розподілу дискретних та неперервних величин.
Закони розподілу дискретних величин.
Біноміальний розподіл (розподіл Бернулі)
Цей
розподіл справедливий тільки до
дискретної випадкової величини Х,
яка може приймати тільки цілі невід'ємні
значення з ймовірностями
![]() ,
де
,
де![]() -
ймовірністьпояви
події в кожному випробуванні, m
- кількість сприятливих подій, n
- загальна кількість випробувань,
-
ймовірністьпояви
події в кожному випробуванні, m
- кількість сприятливих подій, n
- загальна кількість випробувань,
![]()
![]() .
.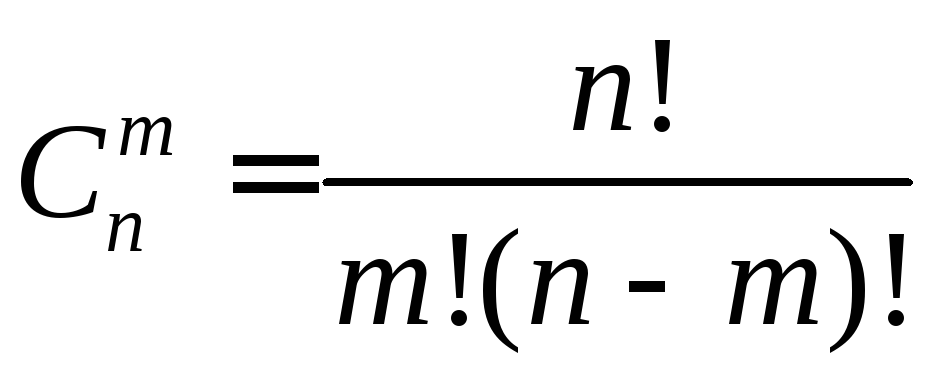 називається розподіленою за біноміальним
законом з математичним сподіванням
називається розподіленою за біноміальним
законом з математичним сподіванням![]() ,
та дисперсією
,
та дисперсією![]() .
.
Закон
Бернулі використовується тоді, коли
необхідно знайти ймовірність появи
випадкової події яка реалізується
рівно
![]() раз у серії з
раз у серії з![]() випробувань.
випробувань.
Біноміальному закону розподілу підпорядковуються такі випадкові події, як число викликів швидкої допомоги за певний проміжок часу, черги до лікаря в поліклініці, епідемії тощо.
Розподіл Пуасона.
Дискретна
випадкова величина X,
яка може приймати тільки цілі невід'ємні
значення з ймовірностями
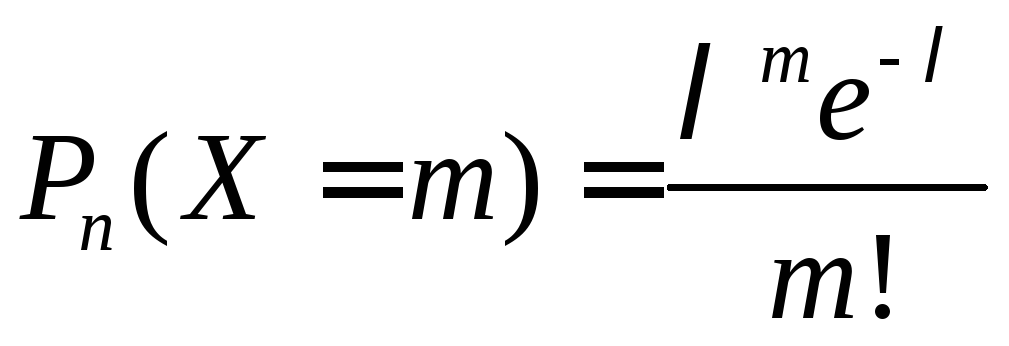 називається
розподіленою за законом Пуассона з
математичним сподіванням
називається
розподіленою за законом Пуассона з
математичним сподіванням
![]() і
дисперсією
і
дисперсією
![]() ,
де
,
де![]() .
Розглядаються малоймовірні події, які
відбуваються у довгій серії незалежних
випробувань декілька разів. Розподіл
Пуасона, як граничний біноміальний
проявляється при розгляді випадкових
процесів дискретної випадкової величиниХ
, яка неперервно залежить від часу. В
медицині використовується при вирішенні
задач надійності медичного обладнання
та апаратури, розповсюдження епідемії,
викликів до хворого дільничних лікарів
та в інших задачах масового обслуговування.
.
Розглядаються малоймовірні події, які
відбуваються у довгій серії незалежних
випробувань декілька разів. Розподіл
Пуасона, як граничний біноміальний
проявляється при розгляді випадкових
процесів дискретної випадкової величиниХ
, яка неперервно залежить від часу. В
медицині використовується при вирішенні
задач надійності медичного обладнання
та апаратури, розповсюдження епідемії,
викликів до хворого дільничних лікарів
та в інших задачах масового обслуговування.
Закони розподілу неперервних випадкових величин
Окрім нормального розподілу, розглянутого вище, в біології та медицині найчастіше розглядають випадкові величині, які можуть мати наступні закони розподілу:
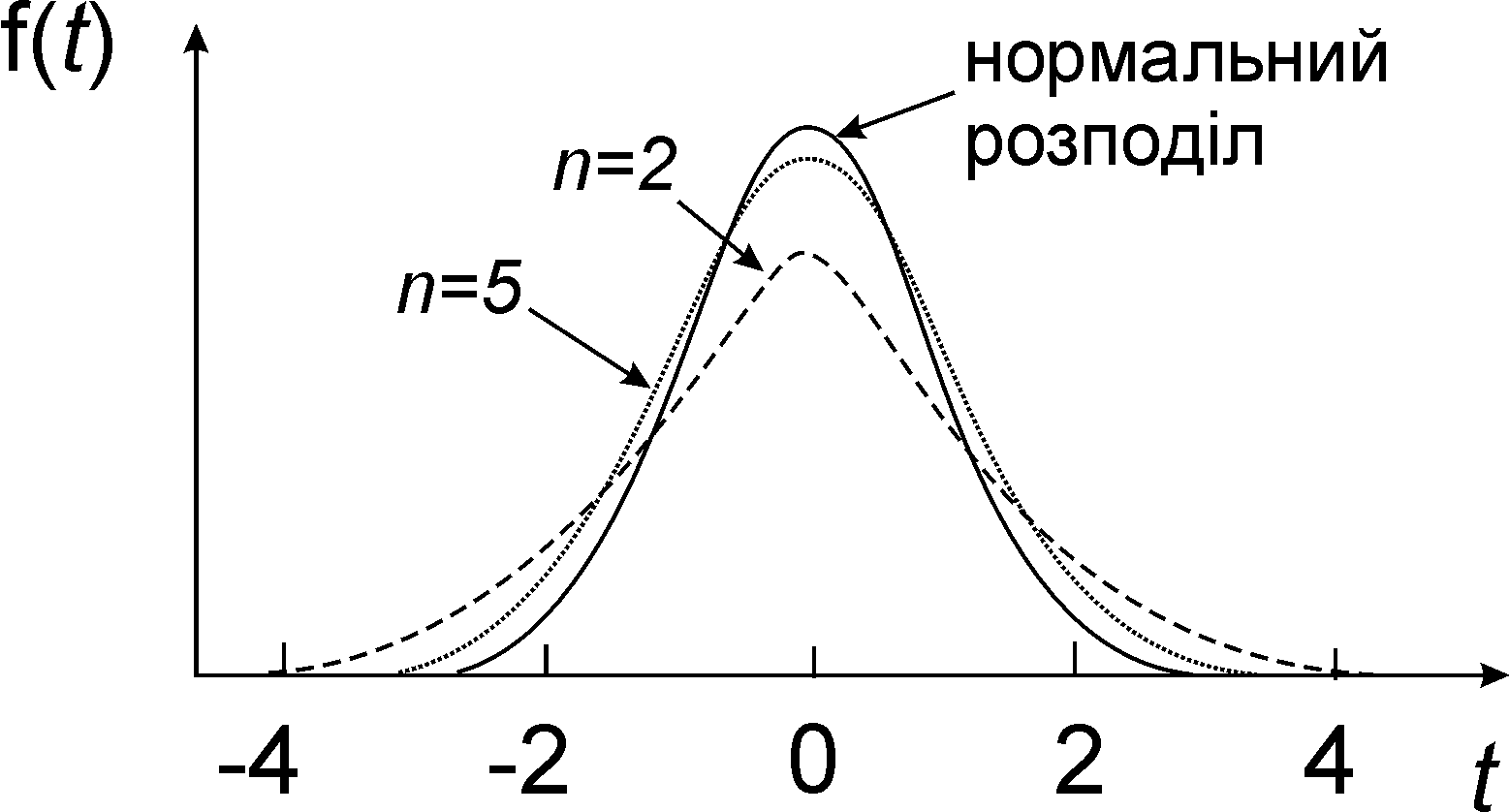
Розподіл Ст 'юдента (Госсета)
Розглянемо
множину результатів
![]() вимірювання
нормально розподіленої величини х
.
З цих даних визначимо
вимірювання
нормально розподіленої величини х
.
З цих даних визначимо
![]() і
і![]() .
Введемо
нову величину
.
Введемо
нову величину
![]() ,
що
містить як експериментальне середнє
значення так і задане значення вимірюваної
величини
,
що
містить як експериментальне середнє
значення так і задане значення вимірюваної
величини
![]() ,
яке
точно відоме, наприклад із розрахунків
та таблиць:
,
яке
точно відоме, наприклад із розрахунків
та таблиць:
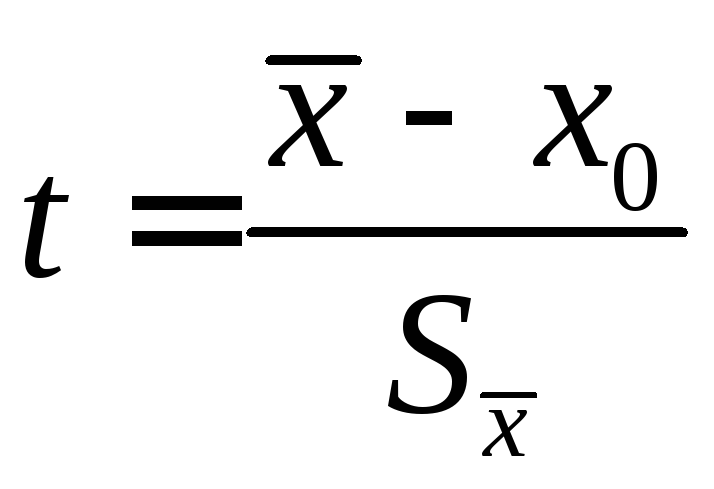 .
.
Тоді
розподіл величини
![]() при
кінцевому числі вимірів п
буде
розподілом Ст'юдента з п
ступенями
вільності або
при
кінцевому числі вимірів п
буде
розподілом Ст'юдента з п
ступенями
вільності або
![]() -розподілом1.
При збільшенні числа ступенів вільності
розподіл Ст'юдента наближається до
нормального. Значення коефіцієнтів
Ст'юдента для відповідної довірчої
ймовірності та кількості ступеней
вільності затабульовані.
-розподілом1.
При збільшенні числа ступенів вільності
розподіл Ст'юдента наближається до
нормального. Значення коефіцієнтів
Ст'юдента для відповідної довірчої
ймовірності та кількості ступеней
вільності затабульовані.
![]() -
розподіл Ст'юдента використовують в
математичній статистиці при визначенні
оцінок ймовірностей попадання випадкової
величини в довірчий інтервал (інтервал,
який із заданою ймовірністю р
покриває
параметр випадкової нормально
розподіленої величини):
-
розподіл Ст'юдента використовують в
математичній статистиці при визначенні
оцінок ймовірностей попадання випадкової
величини в довірчий інтервал (інтервал,
який із заданою ймовірністю р
покриває
параметр випадкової нормально
розподіленої величини):
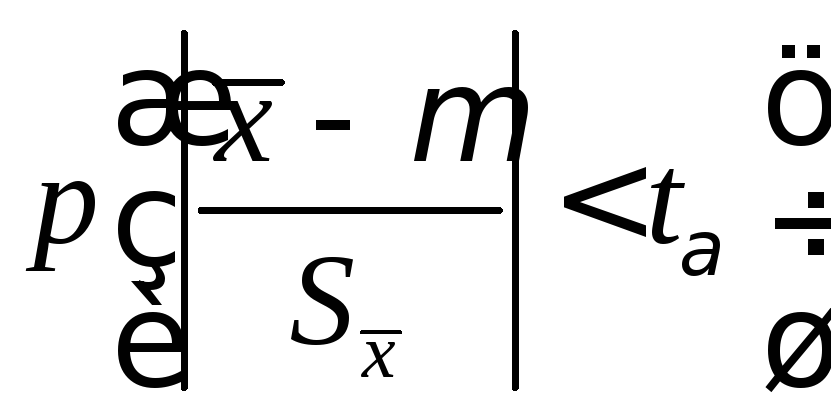 .
.
Математичне
сподівання розподілу Ст'юдента дорівнює
0, а дисперсія-![]() .
.
|
|
|
Рис 8. Розподіл Ст’юдента |
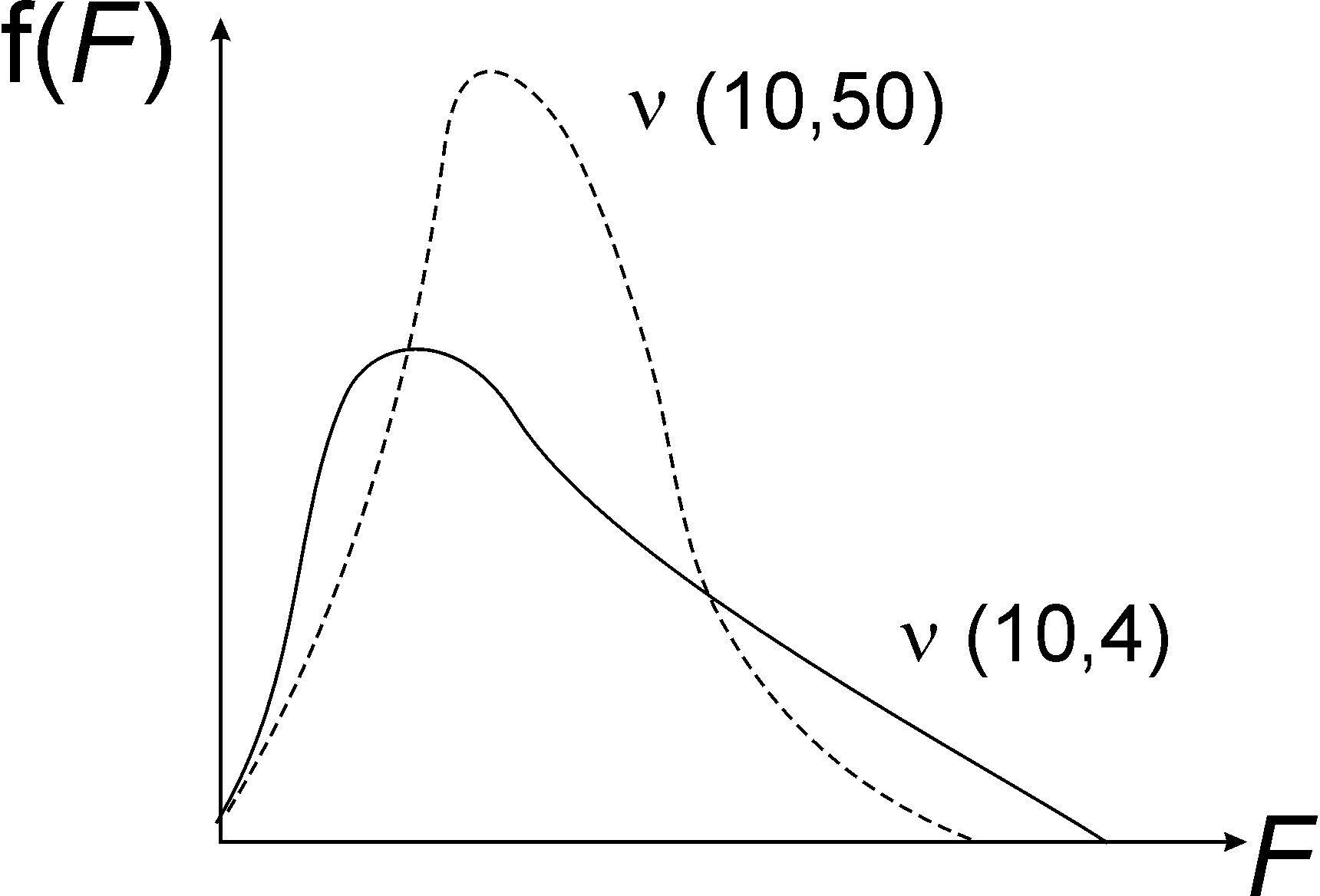
Розподіл Фішера
Нехай
ми провели дві серії незалежних
вимірювань випадкової величини:
![]() і
і![]() з
числом вимірювань в серіях
з
числом вимірювань в серіях
![]() і
і![]() і вибірковими
і вибірковими
|
|
|
Рис 9. Розподіл Фішера |
дисперсіями
![]() і
і![]() відповідно. Тоді розподіл випадкової
величини
відповідно. Тоді розподіл випадкової
величини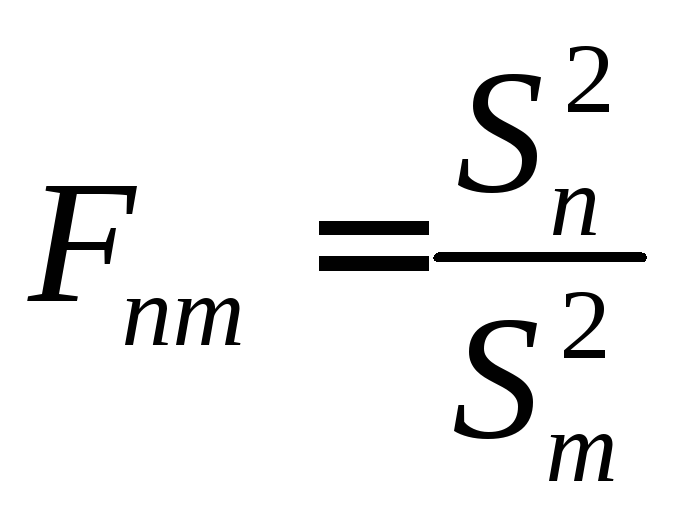 називається розподілом Фішера з (
називається розподілом Фішера з (![]() )
ступенями вільності.
)
ступенями вільності.
Розподіл
![]()
Нехай
маємо вибірку із п
незалежні
випадкових величин
![]() -
розподілених за нормальним законом
з
-
розподілених за нормальним законом
з![]() =0
та
=0
та
![]() .
Якщо для кожної випадкової величини
створимо вираз
.
Якщо для кожної випадкової величини
створимо вираз
![]() то сума квадратів випадкових величин
то сума квадратів випадкових величин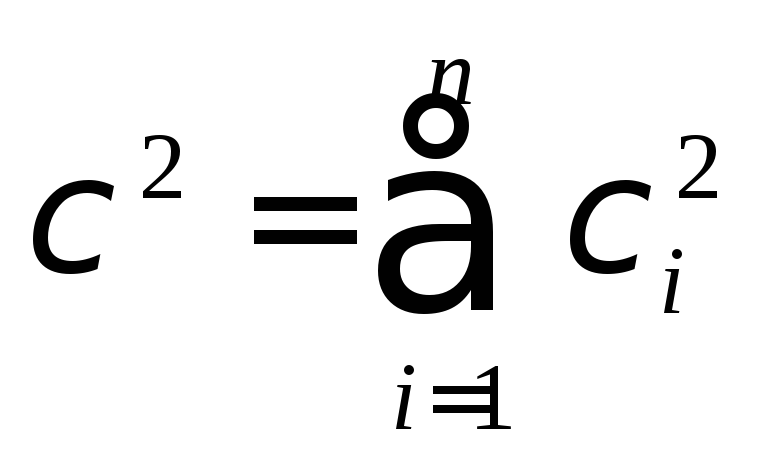 має
закон розподілу, що носить назву
має
закон розподілу, що носить назву![]() -
розподіл з
-
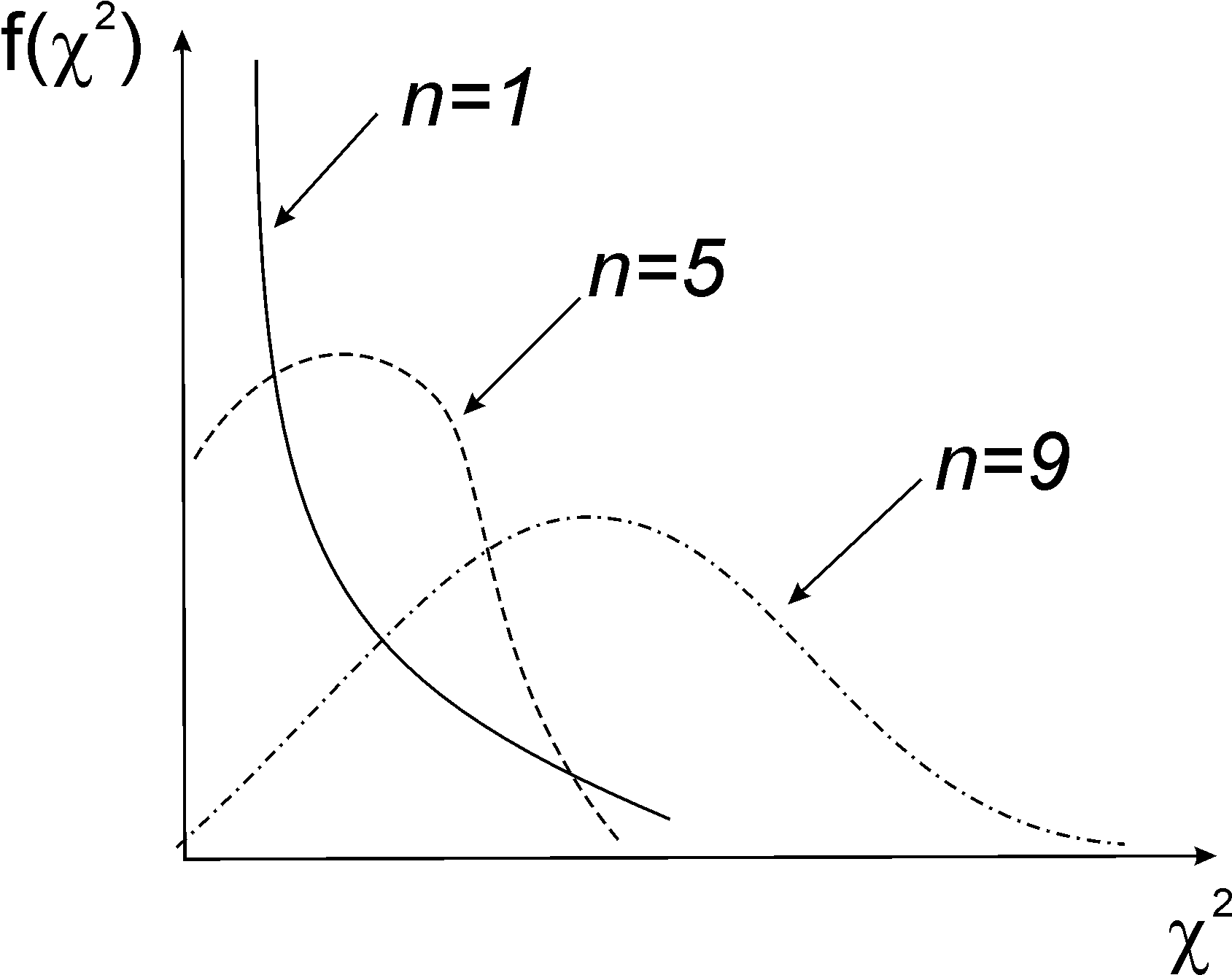
розподіл з![]() ступенями вільності. Із збільшенням
ступенів вільності розподіл
ступенями вільності. Із збільшенням
ступенів вільності розподіл![]() наближається до нормального розподілу.
наближається до нормального розподілу.
|
|
|
Рис
10. Розподіл
|