Интегральное исчисление

БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ

КАФЕДРА “ВЫСШАЯ МАТЕМАТИКА”

ЮДЕНКОВ Ю.Т.

Электронная версия курса математика технического вуза

Часть 3 .

Интегральное исчисление(неопределенный, определенный, криволинейные, кратные).

Пособие разработано на основе лекций, читаемых на протяжении ряда лет студентам специальности АЭП (электропривод)

по дисциплине “ Высшая математика.”

2006 г.

Введение

В основу курса положены лекции и практические занятия, на протяжении многих лет реализованные в учебном процессе для специальности “Электропривод и автоматизация промышленных предприятий”. Расположение материала обусловлено не требованиями математической строгости изложения, но чисто утилитарно, с таким расчетом, чтобы аппарат предыдущих разделов мог служить инструментом для изучения последующих. Именно на таком принципе даны многие формулировки основных понятий и развития приложений, основанных на этих понятиях. Для начинающего напомним, что термин “определение” подразумевает “договор” между читателем и остальными пользователями математики по некоторому вопросу для исключения возможных неверных толкований. Это значит, что для понимания вопросов, следующих за определением, определение должно быть “вызубрено”, но не вспоминаться с напряжением.

`Текст курса написан не языком “чистого математика” (т.е. определение --> теорема и ее доказательство --> следствия --> обобщение --> новое определение и начинаем сначала ...), а языком для математикаприкладника (определения --> вытекающие из него естественным путем выводы (иногда теоремы с доказательствами) --> отработка навыков использования новых понятий и возможностей --> возможные приложения новых сведений --> переход на введение новых понятий). В текстах сравнительно мало примеров, т.к. это – фактический конспект лекций. Для более полного понимания изучаемого материала предполагается, что читатель будет иметь удовольствие полистать литературу по изучаемому вопросу. Список учебной литературы не приводится из-за его объемности, а также по той причине, что каждый лектор придерживается своего перечня книг. Все приведенные тексты – компиляция книг разных авторов, разного времени издания и разного назначения. Данный курс построен по принципу “понятно лектору – будет понятно и слушателю” и потому представляет собой лоскутное одеяло из разных разделов математики, изложенных в разном стиле. При этом везде преследовалась цель изложения математических принципов в прикладной направленности. Это обнаруживается в большом числе комментариев к теоремам, доказательствам и следствиям.

1.Неопределенный интеграл

1.1.Первообразная. Неопределенный интеграл и его свойства

Опред. F(x) называют первообразной f(x) (для f(x)) на [a;b] , если для любого х из этого отрезка F(x) дифференцируема и F’(x)=f(x). (По Садовничеву, Сендову стр 314).

Так F(x)=2x будет первообразной f(x)=x2 для всех действительных чисел.

Теорема. Если F1(x) и F2(x) первообразные f(x) на [a;b] , то любого х из этого отрезка имеет место равенство F1(x) - F2(x) =С .

Док. Положим Ф(х)= F1(x) - F2(x). Тогда Ф(х) дифференцируема и Ф’(х)=0. Т.е. Ф(х)=С. Откуда и следует вывод.

Следствие. Если F(x) одна из первообразных для f(x) то любая Ф(х)=F(x)+C – тоже первообразная.

Так Ф(x)=2x +С будет первообразной f(x)=x2 для всех действительных чисел. Опред. Множество первообразных для данной f(x) на [a;b] называют

неопределенным интегралом и обозначают ∫f (x)dx .

Из определения следует справедливость тождества ∫ f (x)dx =F(x)+C.

Термины и обозначения: f(x) - подынтегральная функция; f(x)dx – подынтегральное выражение; х ( записанный в символе dx) - аргумент

(переменная) интегрирования; ∫ - символ интегрирования.

Все рассмотренное – процесс, обратный поиску производной. Следствия.

1.Производная от НИ равна подынтегральной функции (∫ f (x)dx)' ’=f(x).

2.Дифференциал от НИ равен подынтегральному выражению d (∫ f (x)dx)'

=f(x)dx.

3.Неопределенный интеграл от производной равен подынтегральной функции с точностью до постоянного слагаемого С. ∫ F’(x)dx= F(x)+C.

4.Неопределенный интеграл от дифференциала равен выражению под знаком дифференциала точностью до постоянного слагаемого С. ∫ dF(x)=

F(x)+C.

Все это разные вариации определения. Свойства.

1.Константу - множитель можно выносить из-под знача НИ.

∫кf (x)dx =кF(x)+C.

Док. Пусть F(x) – первообразная для f(x). Т.е. F’(x)=f(x). Тогда кF(x) –

первообразная для кf(x), т.к. (кF(x))’= кF’(x)= кf(x). Т.е. к∫f (x)dx =к(F(x)+C)=

кF(x)+C= ∫кf (x)dx . (Или просто продифференцировать обе части равенства). 2.НИ от суммы функций равен сумме интегралов от слагаемых.

∫( f (x) +ф(х))dx =

∫f (x)dx + ∫ф(x)dx .

Док. Пусть F(x) и Ф(х) – первообразные, соответственно, для f(x) и ф(х). Тогда F’(x)=f(x) и Ф’(х)=ф(х) и потому F(x) ± Ф(х) – первообразная для

f(x) ± ф(х). Откуда ∫ f (x)dx ± ∫ф(x)dx = F(x) +С1 ± Ф(х)+С2 F(x) ± Ф(х) +С= ∫( f (x) ± ф(х))dx .

3.Независимость от аргумента. ∫f (x)dx = ∫f (u)du = ∫f (Cosx)dCosx = F(x)= F(u)= F(Cosx) .

Комментарий. В отличие от производных, где каждой ситуации предписано правило ее обработки, при поиске интегралов вся теория заканчивается на этой таблице. Фактически для поиска интеграла остаются только определение и следствия из него, свойства и таблица. А это значит, что все остальное следует преобразовывать эвристическими приемами (или по уже готовым рекомендациям, но не правилам!) к таблице и определению. В качестве контроля ответа может служить только обратный процесс – от результата возьми производную. И, если результат равен подынтегральной функции, то имеется некоторая степень уверенности в правильности выполнения интегрирования.

1.2.Методы интегрирования.

Пусть х=ф(t) –монотонная и непрерывная на некотором промежутке функция. Если на соответствующем промежутке изменения переменной х

функция f(x) интегрируема, то справедливо равенство ∫f (x)dx = ∫ f (ф(t))ф'(t)dt .

Записанное равенство называют формулой замены в неопределенном интеграле. Применяют ее тогда, когда правая часть оказывается ближе к табличному интегралу (см. Комментарий выше).

Док. В самом деле, т.к. F(x) - первообразная для f(x), то F(ф(t)) – будет первообразной для f(ф(t))ф’(t). И потому F’(ф(t))= F’ф(ф(t))ф’t(t)= f(ф(t))ф’(t).

Откуда следует f(ф(t))ф’(t)dt= F(ф(t))+C= F(x)+C= ∫f (x)dx .

Комментарий. Имеются два подхода использования формулы замены. Один из них изложен выше. В другом (более употребимом) случае заменяют не переменную х на некоторое выражение, а выражение, связывающее х, заменяют одной переменной. А далее – как обычно.

= ∫ Costdt=-Sint +C= -Sinlnx +C.

Иногда замену переменных используют в еще одном виде – подведении под знак дифференциала, используя простое соотношение

dx= 1а d(ax+b) для любых а≠ 0 и в. По знак дифференциала подводят такую

группу, чтобы интеграл сменил аргумент интегрирования (см. следствия из определения) и при этом принял табличный вид .

совпадает с примером 7.1.

Пусть каждая из u(x) и v(x) дифференцируемы на некотором промежутке и существует первообразная для произведения u’(x)v(x). Тогда на этом промежутке существует первообразная для u(x)v’(x) и справедливо равенство

∫ udv = uv - ∫ vdu , называемое формулой интегрирования по частям.

Док. Имеем равенство (uv)’=u’v+v’u. Проинтегрируем его и получим uv = ∫ vdu+ ∫ udv . Откуда легко получить требуемое.

Комментарии.

1. Рекомендации по применению этой формулы.

Т.к. теорема доказана в общем случае, то применять ее можно всегда. . Однако наибольшего эффекта можно добиться, если применять ее , когда под интегралом записано произведение функций Pn(x)eax ; Pn(x)Sinkx (или другая тригонометрическая функция); eaxCoskx (или другая триг. функция ); Pn(x)lnbx и т.д.

2.Возможно одного шага применения формулы недостаточно. Тогда ее приме-

няют кратно.

3.Возможно применение формулы приведет к сохранению подынтегрального

выражения. Не следует тревожиться по такому случаю, т.к. это даже хорошо.

4.Выбор частей u и v основан на опыте. Только решение конкретных примеров обеспечит навыком выбора частей.

Пример 7.3. Простой интеграл ∫ xdx при выборе частей u=x, dv=dx откуда du=dx и v=x приводит нас по формуле интегрирования по частям а равенству ∫ xdx =х2 + ∫ xdx. Откуда следует равенство 2 ∫ xdx = х2 . Откуда

∫ xdx = х2 /2+C.

1.3.Некоторые классы интегрируемых функций.

Т.к. в практических приложениях предстоит интегрировать выражения разной сложности, то следует научиться отличать, то что приводит к конкретному ответу от того, что ни при каких услиях не приведет к результату. Умению отличать одно от другого и приемам интегрирования посвящен данный раздел.

Рассмотрим некоторые классы функций, для которых опытным путем разработаны приемы отыскания неопределенных интегралов. Фактически приемы эти приводят к таблице основных интегралов. Отметим также, что в интегральном исчислении принята такая схема работы – если новый , ранее неизвестный интеграл преобразован к уже известному классу, задача считается решенной.

1.3.1.Рациональные дроби.

Определение. Рациональной дробью называют выражение QPn ((xx)) . Где

m

где квадратные трехчлены в знаменателях не имеют действительных корней. Интегралы от простейших дробей находят по таким схемам.

I-й тип. Вынесем за знак интеграла константу А и подведем под знак

II-й тип обработаем аналогично I-му. Но используем интеграл от степени. III-й тип. Обрабатываем в несколько приемов.

1-й. Сначала найдем производную от знаменателя 2x+p.

2-й шаг. Если в числителе С не нуль, то преобразуем числитель к виду суммы производной от знаменателя и константы Cx+D= C2 (2x+p)+D- Cp2 .

3-й шаг. Разобьем исходный интеграл на сумму двух интегралов, числитель первого – производная 2х+р; числитель второго – константа

4-й шаг. После подведения числителя 1-го слагаемого под знак интеграла первое слагаемое дает табличный интеграл от логарифма знаменателя. Во втором слагаемом в знаменателе выдели полный квадрат в трехчлене и тогда

Комментарий. Рекомендуется не запоминать окончательный ответ (хотя и не возбраняется), а пройти на паре примеров весь алгоритм. Этого будет достаточно для усвоения процесса. Этот процесс встречается очень часто в других разделах математики и других дисциплин (ТОЭ, механика, сопромат).

IV-й тип обрабатывается по схеме типа III . Только в конце всегда получается типовой интеграл, который обрабатывают по рекуррентной формуле

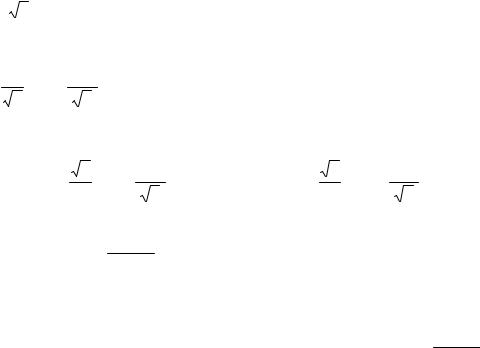
Первый интеграл сохранить, т.к. в нем степень знаменателя понижена. Во втором интеграле применить формулу интегрирования по частям, выбрав u=t остальное dv. И тогда степень знаменателя понизится. Затем привести подобные по интегралам с одинаковыми знаменателями степени k-1.

Подынтегральное выражение – простейшая дробь 4-го типа, т.к. трехчлен не имеет действительных корней. Производная от трехчлена равна 2х+2. Преобразованный числитель имеет вид 0,5(2х+2) –2, а подынтегральная

Далее первый интеграл дает после подведения под знак дифференциала 2х+2

Во втором интеграле в знаменателе выделим полный квадрат и преобразуем аргумент интегрирования – подведем под знак дифференциала константу 1.

Теперь строим алгоритм интегрирования рациональной дроби.

1-й шаг. Проверяем, будет ли QPn ((xx)) правильной (будет ли m>n)? Если будет,

m

то переходим к шагу 3. Иначе выполняем шаг 2.

2-й шаг. Делим числитель на знаменатель ‘уголком’. Представляем неправильную дробь в виде суммы целой части и правильной дроби QR(x()x) .

m

От целой части берем интеграл как о суммы степеней. Для отыскания интеграла от правильной дроби выполняем шаг 3.

3-й шаг. Находим корни полинома Qm(x) и разлагаем его на множители

Qm(x)=(x-a)k1(x-b)k2…(x-c)k3(x2+p1x+q1)k4+(x2+p2x+q2)k5+…+(x2+p3x+q3)k6 .

При этом k1+k2 +… +k3 +2k4 +2k5 +…2k6 =m , а числа этом k1, k2 ,… , k3, k4 , k5 , …,k6 - кратности корней.

Продолжаем работу. Приведем справа к общему знаменателю и

=А(х-2)(х+2)+Вх(х+2)+Дх(х-2).

В последнем равенстве можно справа раскрыть скобки и сгруппировать слагаемые по степеням х; затем приравнять коэффициенты при одинаковых степенях слева и справа. Можно в обе части подставить некоторые значения аргумента х. Выполним для контроля оба эти действия. При этом скобок раскрывать не будем, а сделаем это устно. Приравняем коэффициенты при х2

. Слева коэффициент при этой степени 9. А справа эта степень будет записана с коэффициентом (А+В+Д) , что можно увидеть сразу. Теперь коэффициенты при х : слева –2, а справа 2В-2Д. Теперь при хо (свободные

Если же мы подставим в обе части равенства полиномов последовательно

упрощать.

1.3.2.Рациональные тригонометрические функции.

Рациональным тригонометрическим выражением называют выражение типа R(Sinx, Cosx). Рассмотрим простейшие приемы интегрирования таких

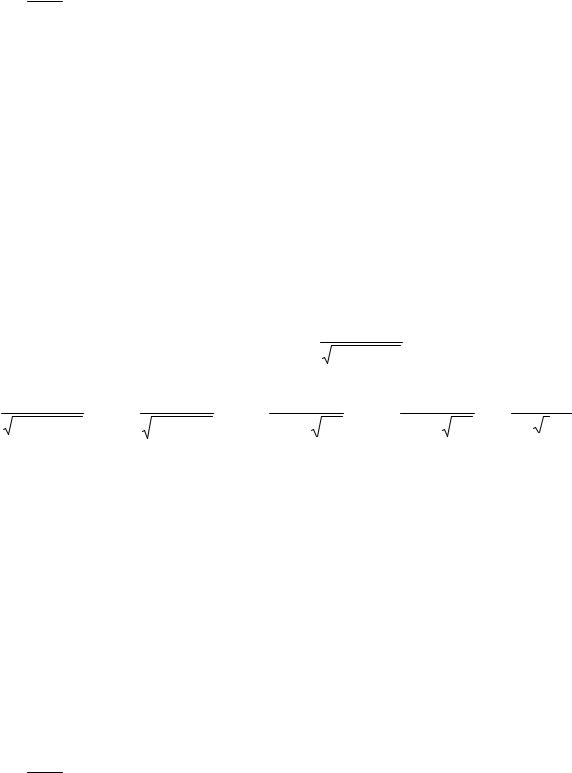
и dx=12+dtt 2 , то мы привели интеграл от тригонометрического выражения к

интегралу от рац. дроби. Дальнейшие действия см.выше.

Если под интегралом записаны произведения вида SinaxCosbx ; SinaxSinbx; CosaxCosbx , тогда произведение разворачиваем в сумму и получаем табличные интегралы.

Если под интегралом записаны выражения вида SinkxCoslx , то поступают так:

если k и l четные числа, то используют формулы понижения степени

Sin2x=0,5(1+Cos2x); Cos2x=0,5(1-Cos2x). Затем обрабатывают полученное;

если k четное, а l нечетное (или наоборот), то “отсчепляют” от нечетной степени основание и подводят его под знак дифференциала, а все четные степени выражают через функцию, записанную под знаком дифференциала;

если k+l – четное отрицательное целое, то применяют подстановку tgx=t и получают табличные интегралы.

1.3.3.Простейшие иррациональные выражения.

Рациональным тригонометрическим выражением называют выражение типа R(Sinx, Cosx). Рассмотрим простейшие приемы интегрирования таких

и dx=12+dtt 2 , то мы привели интеграл от тригонометрического выражения к

интегралу от рац. дроби. Дальнейшие действия см.выше.

Если под интегралом записаны произведения вида SinaxCosbx ; SinaxSinbx; CosaxCosbx , тогда произведение разворачиваем в сумму и получаем табличные интегралы.

Если под интегралом записаны выражения вида SinkxCoslx , то поступают так: