Интегральное исчисление

Обобщая решения этих задач дадим определения для кратных интегралов.

Пусть в некоторой области D c границей Г задана непрерывная f(M). Разобьем D на части достаточно малого размера (диаметра). Но каждом участке разбиения выберем точку Mk, вычислим и составим сумму

пределы существуют независимо от способа разбиения области D на части и выбора точки Mk на каждой части разбиения, то назовем эти пределы

соответственно двойным и тройным интегралом и обозначим ∫∫f (M )dο и

D

∫∫∫f (M )dv .

D

Для большего отличия в записи двойного и тройного интегралов последний часто обозначают ∫∫∫f (M )dv и тогда сразу видно, что

V

интегрирование ведется по пространственной мере, в то время как в двойном

– по плоской. Оба интеграла называют общим термином – кратный интеграл, если нет крайней необходимости выделить что-то особенное . Из получения интегралов следует, что теорема существования и основные свойства их повторяют свойства определенного. Выделим особо некоторые из этих свойств, т.к. они отличаются написанием. Так, теорема об оценке интеграла

D

D, а SD – площадь D. Соответственно изменятся термины для тройного интеграла. Поэтому в дальнейшем все выкладки будем делать, опираясь на двойной интеграл (ДИ), а результаты переносить на интеграл любой кратности, если нет существенных отличий.

4.2.Вычисление кратных интегралов в декартовых координатах.

Пусть требуется вычислить ∫∫f (M )dο от знакоположительной

D

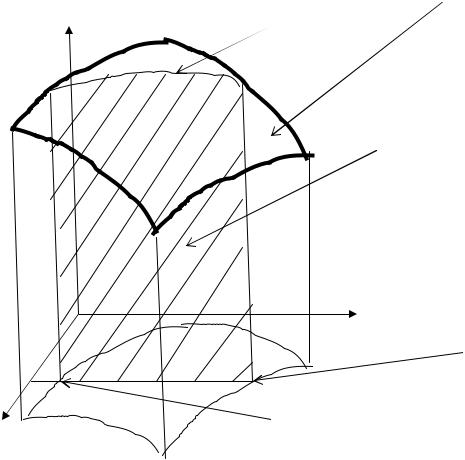
непрерывной f(M) по области D, расположенной в плоскости хОу. Изобразим цилиндроид для облегчения рассуждений.

Z=f(x;y)

Z=f(xo;y)

криволинейная

трапеция

у

точка выхода на y=y2(x)

Х=хо

Рис 13.1. К расстановке пределов интегрирования в ДИ.

Проведем сечение цилиндроида плоскостью х=хо . При этом цилиндроид будет рассечен по криволинейной трапеции. Площадь ее

y2 ( xo )

выражается определенным интегралом S(xo)= ∫ f (xo ; y)dy . Т.к. хо взято

y1 ( xo )

произвольно, то фактически имеем зависимость S (x). И тогда можно вычислить объем тела по площадям параллельных сечений из определенного

интеграла V= ∫b S(x)dx =

называть повторным или двукратным интегралом. В этом интеграле [a;b] – проекция области D на ось Ох – пределы внешнего интеграла; y1(x), y2(x) – пределы внутреннего интеграла (они получены, если решить уравнение границы относительно переменной у для точек входа и выхода).

Теперь остается вычислить двукратный интеграл, начиная с внутреннего интеграла по формуле Ньютона-Лейбница в предположении, что х постоянная величина. Затем от полученного результата вычислить определенный интеграл по той же формуле. Это и будет ответ.

Наиболее распространенной при вычислении ДИ является полярная система координат x = ρ Cos ϕ , y = ρ Sinϕ . Легко вычислить якобиан J= ρ ≠ 0 .

Комментарий. Следует быть осмотрительным при расстановке пределов интегрирования в ДИ в полярной системе координат по известному алгоритму. Дело в том, что проектирование там реализуется не параллельное (перпендикулярное) , а центральное (система то полярная). Поэтому внешний интеграл всегда берут по переменной ф и проектирование идет в секторе изменения угла. А далее как обачно, т.е. в секторе проводят луч (аналог перпендикуляра). И еще. При построении D в полярной системе следует помнить, что ρ - это расстояние и оно неотрицательно.

повторного не представляет труда, отметим, что он в декартовых координатах будет неберущимся. Сделаем переход к полярным координатам

При вычислении тройных интегралов используют цилиндрическую или сферическую систему координат. Формулы перехода для цилиндрической

следует быть внимательным к последним формулам. В них формулы могут быть иными, в зависимости от того, как отсчитывают угол Θ. Его можно отсчитывать от плоскости ХОУ (от горизонта, угол места у артиллеристов и топографов) или от вертикали (угол склонения у астрономов). На основании этих формул получим разные по виду якобианы.

4.4.Приближенное вычисление кратных интегралов.

Ограничимся случаем ДИ. Если вычислить ДИ в квадратурах затруднительно, используют приближенные методы. Чаще всего для оценки используют метод Монте-Карло. Он основан на простом принципе. Пусть имеется квадрат со стороной 1 и в нем расположена некоторая область D. Предположим, мы бросили в квадрат N случайных равномерно распределенных точек. Естественно, часть из них попадет в D. Тогда площадь области можно приближенно подсчитать в виде отношения n/N, где n –число точек, оказавшихся внутри D.

Реализуется метод в такой последовательности.

Сначала нормализуют область интегрирования D(располагают ее в единичном квадрате, с левой нижней вершиной в начале координат и сторонами , расположенными вдоль осей х и у). Если область не нормализована (не располагается где требуется) , то это всегда можно

сделать заменой переменных x=a+u(b-a), y=c+v(d-c), где u,v– новые переменные, [a;b] - проекция D на Ох, [c;d] - проекция D на Оy. Якобиан такого перехода (замены) равен (b-a)(d-c) гарантировано не равен нулю. Сделав такую замену, генерируют N случайных точек, равномерно распределенных в единичном квадрате и подсчитывают число n точек, оказавшихся в области D. Затем записывают теорему о среднем для ДИ

∫∫f (u, v) d σ =f(C)SD . С – точка в области D, SD - площадь области D. Т.к.

поручить ЭВМ. Но вся интеллектуальная подготовка остается за исполнителем.

4.5.Приложения кратных интегралов.

Исходя из задач, приводящих к понятию кратных интегралов, получаем схему их применения при решении прикладных задач.

Сначала устанавливают физическую или математическую формулу для работы и анализируют возможность ее применения. Находят характеристику, изменение которой влияет на изменение искомой величины. Область задания разбивают на частицы достаточно малого размера с таким расчетом, чтобы на каждой части выбранная характеристика практически не менялась. Вычисляют интересующую величину на выбранной части разбиения. После суммирования получают кратный интеграл.

По такой схеме можно вычислять объем пространственного тела как разность объемов двух цилиндроидов, представленных двойными интегралами.

Этот же объем можно вычислить тройным интегралом, если положить подынтегральную функцию равной 1. В этом случае масса тела, представленная тройным интегралом, численно равна объему этого тела.

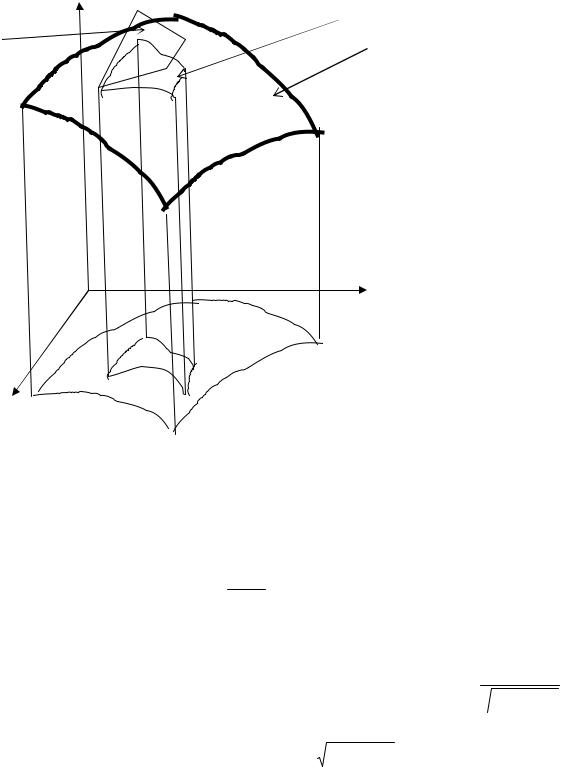
Несколько сложнее вычислять площадь поверхности, заданной функцией 2-х переменных z=f(x;y). Руководствуемся Рис 13.3 и рассуждаем так. Известно, что площадь проекции некоторой плоской фигуры равна

площади самой фигуры на косинус угла между плоскостями Sпроекции=Sфигуры

Cosф.

z=f(x;y)

у

Х dσ

Рис 13.3. К вычислению площади поверхности

Выделим на поверхности небольшую часть. Пусть ее площадь равна ds нам неизвестна. Возьмем точку на этой площадке и проведем касательную плоскость Т к поверхности в этой точке. При малых ds можно считать приближенно равными ds и расположенную над ней dT. В свою очередь между dT и dσ как проекцией dT на плоскость хОу имеем соотношение

dσ =dTCosф. Отсюда получаем ds= cosd σϕ . Но ф – это угол между нормалями к

→

касательной плоскости Т и плоскости хОу. Нормалью к хОу служит вектор k , а нормалью к поверхности z=f(x;y) служит, как известно, вектор градиента,

−1

который в нашем случае равен ( zx' ; z 'y ;−1). Поэтому Cosф= zx' + z'y +1 . Подставим полученное значение в формулу для вычисления ds. Затем проведем интегрирование и получим S= ∫∫ zx' + z'y +1 d σ - формула для

D

вычисления площади поверхности двойным интегралом.

При решении физических задач используем известные определения: масса однородного объекта с плотностью ρ вычисляется по формуле m= ρ V;

статический момент относительно оси (точки) вычисляется по формуле М=mr (где m – масса, сосредоточенная в точке, r -расстояние от этой массы до точки или оси ); кинетический момент (момент инерции) J=mr2 (m,r смотри выше) и т.д.

Если же тело или масса неоднородны(или размеры массы соизмеримы с расстоянием r), то следует объект разбить на части достаточно малого размера и вычислять dm, dM или dJ, а затем переходить к соответствующему интегралу.