
Интегральное исчисление
.pdf
Именно при таком негласном (default) определении была вычислена площадь криволинейной трапеции.
Отсюда следует, что площадь произвольной фигуры можно вычислить как разность двух площадей криволинейных трапеций . У этих трапеций общее основание, боковые стороны. А отличаются они верхней стороной. У большей из трапеций верхняя сторона f2(x) , а у меньшей – f1(x). В
результате площадь произвольной фигуры равна ∫b ( f2(x)- f1(x))dx .
a
Если же фигура задана криволинейным треугольником ОАВ в полярной системе координат Рис 7.1, то поступаем так : в секторе изменения угла ф,
|
А |
|
ф |
занимаемом треугольником |
||
|
|
|
|
ОАВ проведем два достаточ- |
||
|
|
|
|
но близких луча, угол между |
||
|
|
|
В |
которыми равен |
ф. Тогда |
|
|
|
|
|
площадь выделенного сек- |
||
|
ρ = ρ(ф) |
|
тора приближенно |
|||
О |
|
|
|
поляра |
|
|
|
Рис 7.1. К вычислению площади. |
|
|
|||
равна S=0,5 ρ(ф)2 Sin |
ф= |
0,5 ρ(ф)2 |
ф , ввиду того, что при малых |
|||
изменениях |
ф величина |
ρ(ф) остается практически неизменной (одно из |
||||
требований к величине Q см. общую постановку), а Sin |
ф эквивалентен ф |
|||||
при малых |
значениях |
ф. |
После суммирования и |
перехода |
к пределу |
|
получаем формулу для вычисления площади криволинейного треугольника
ОАВ в полярной системе координат SOAB=0,5 ∫b |
ρ(ф)2 ф. Эту формулу |
|
|
a |
|
легко обобщить на произвольную фигуру в полярной системе координат S= |
||
0,5 ∫b |
( ρ2 (ф)2 - ρ1 (ф)2 ) ф. |
|
a |
|
|
2.6.2.Вычисление длин дуг плоских кривых.
Пусть дана дуга плоской кривой y=f(x) от точка А(х1,f(x1)) до точки В(х2,f(x2)). Впишем в эту дугу ломаную и подсчитаем периметр ломаной.
Опр. Если существует предел периметров ломаных, вписанных в дугу, когда число звеньев ломаной неограниченно увеличивается, а максимальная длина звена ломаной неограниченно уменьшается, то дугу назовем спрямляемой (имеющей длину), а этот предел назовем длиной дуги.
По этому определению длина дуги отвечает всем требованиям для применения ОИ.

А
|
у |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
В |
|
|
О |
|
|
х |
|
|
|
х |
|
|
|
|
|
|
|
|||||
|
Рис 7.2. К вычислению длины дуги плоской кривой. |
||||||||
Выберем одно достаточно малое звено ломаной l. Тогда получаем |
|||||||||
равенство |
l= x2 + y 2 = х 1+ |
y 2 |
= х 1+( y')2 |
. После суммирования и |
|||||
x2 |
|||||||||
|
|
|
|
|
|
|
|
||
перехода к пределу в сумме получим формулу для вычисления длины дуги
заданной кривой L= x∫2
|
|
|
x1 |
|
Если |
же |
|
дуга |
|
l= x2 + |
y 2 = |
t |
x2 |
|
t 2 |
||||
|
|
|
1+( f '(x))2 dx.
|
|
|
|
|
|
|
|
|
|
|
|
|
кривой |
задана |
параметрически |
y = y(t), |
, |
то |
|||||
|
x = x(t) |
||||||||||
+ |
y 2 |
= |
t (x' |
)2 |
+ ( y' |
)2 |
. После суммирования |
и |
|||
t 2 |
|||||||||||
|
|
t |
|
t |
|
|
|
|
|
||
перехода к пределу в сумме получим формулу для вычисления длины дуги
заданной кривой L= t∫B (xt' )2 +( yt' )2 dt.
tA
Если же кривая задана в полярной |
системе координат |
уравнением |
|||
ρ = ρ(ф) , |
то |
сначала |
вычислим |
приближенное |
значение |
х=x’(ф)dф=( ρ Cosф)’фdф=( ρ ’фCosф - ρ Sinф)dф, т.к. х= ρ(ф) Cosф. Затем у=у’(ф)dф=( ρ Sinф)’фdф=( ρ ’фSinф + ρ Cosф)dф, т.к. y= ρ(ф) Sinф.
имеем |
|
равенство |
|
l= |
x2 + y 2 = ( ρф' Cosф − ρSinф)2 |
+( ρф' |
Sinф + ρ Cosф)2 dф |
или |
после |
преобразования под корнем |
l= |
( ρф' )2 + ρ2 dф. Если |
теперь |
полученное |
просуммировать и перейти к пределу, то получим формулу для вычисления
длины дуги заданной кривой L= ф∫B |
( ρф' )2 + ρ2 dф. |
фA |
|
2.6.3.Вычисление объемов.
Понятно, что объем – величина аддитивная. А в качестве характеристики , изменяемой от некоторой координаты, можно взять площадь поперечного сечения при удачном выборе системы координат см. Рис.7.3.

V
А
|
|
S(xo) |
у |
|
|
О |
хo |
х |
Рис 7.3. К вычислению объема тела. |
||
Подведем к телу |
ось |
Ох. В произвольной точке xo проведем |
поперечное сечение тела. Если нам удается выразить площадь поперечного сечения S как функцию координаты точки сечения S(xo), то можно продолжить решение задачи. Т.к. Два достаточно близко расположенных сечения приближенно имеют одинаковую площадь, то объем V, заключенный между этими сечениями приближенно равен S(xo) х. Просуммируем такие объемы и вычислим предел полученной суммы, когда
число сечений растет неограниченно, а максимальное х |
неограниченно |
уменьшается. Получим формулу для вычисления объема V= ∫b |
S(x)dх, где a и |
a |
|
b - крайние точки проекции тела на ось Ох. |
|
Пример 7.8. Вычислить объем цилиндрического отрезка радиуса R и высотой H. Цилиндрический отрезок – это тело, ограниченной прямым круговым цилиндром, поперечным сечением и сечением, проходящим через диаметр поперечного сечения по некоторым углом к поперечному сечению.
Решение. Направим ось Ох вдоль диаметра поперечного сечения, Оу – через центр поперечного сечения перпендикулярно его диаметру, а Оz - через центр поперечного сечения перпендикулярно сечению Рис 7.4. если провести в точках х и О два параллельных сечения, то из подобия треугольников получим
|
|
|
|
|
z |
H |
|
|
|
-R |
y |
|
|
|
|
|
х |
R |
||
|
|
|
|
|
О |
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
Х |
z |
= |
H |
откуда z= |
yH |
, но у= |
R2 − x2 , поэтому z= HR R2 − x2 . А это означает, |
y |
R |
R |
||||
что площадь поперечного сечения цилиндрического отрезка при выбранной
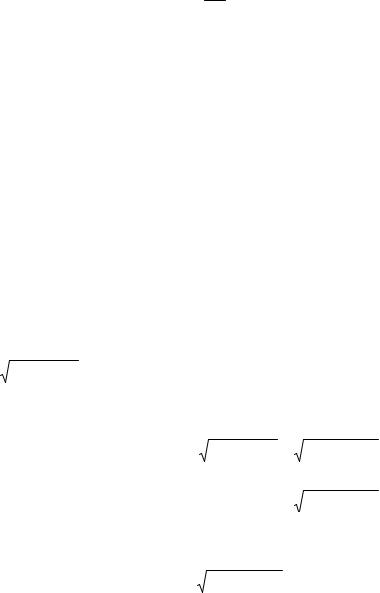
системе координат выражается формулой S(x) =yz= 2HR (R2 − x2) , т.е. является функцией координаты х. А потому объем цилиндрического отрезка равен
V= ∫b |
H |
(R2 − x2) dx = |
H |
(xR2 − |
x3 |
) |
|
a2 |
= |
2H |
R2 . |
|
|
||||||||||||
2R |
2R |
|
|
|||||||||
a |
|
3 |
|
|
|
|
3 |
|
||||
2.6.4.Площадь поверхности вращения.
Опр. Договоримся называть площадью поверхности вращения предел, к которому стремится площадь поверхности, образованной вращением ломаной , вписанной в кривую, вращение которой дает поверхность вращения при условии, что число звеньев ломаной растет неограниченно, а размер звена стремится к нулю.
В такой постановке площадь поверхности обладает свойством аддитивности и можно продолжать рассуждения. Пусть вращается линия y=f(x), непрерывная на [a;b] и осью вращения будет ось Ох.
Разобьем дугу кривой точками на n частей и впишем ломаную. Пусть xi - абсциссы вершин ломаной. Каждое звено ломаной опишет боковую поверхность усеченного конуса, которая равна
Si=2 π |
f (xi−1 ) − f (xi ) |
x2 + y 2 . |
|
|
|
|
|
2 |
f (xi−1 ) − f (xi ) |
|
|
||||
|
|
|
|
||||
Можно приближенно считать, что |
=f(ci) , |
где ci - где-то |
|||||
|
|||||||
|
|
|
2 |
|
|
|
|
между точками xi-1 и xi |
. Ранее было получено |
x2 + y 2 |
= 1+( f '(x))2 dx. |
||||
После чего получаем приближенное значение площади части поверхности вращения, образованной вращением звена ломаной Si=2π f(ci) 1+( f '(x))2 dx.
После суммирования и перехода к пределу при известных ранее условиях получаем формулу для вычисления площади поверхности вращения линии
y=f(x), заданной на [a;b] около оси Ох S=2π ∫b f(x) 1+( f '(x))2 dx.
a
Для других способов задания линии, вращений которой образует поверхность, формулу можно получить аналогично.
2.6.5.Решение физических задач.
При решении физических задач, помимо проверки вычисляемой величины на аддитивность потребуется опорная физическая формула. И лишь после этого начинается подготовка к применению ОИ.
Например, при вычислении статического момента некоторой массы относительно оси или точки используют факт аддитивности статического момента. Помимо этого берут в основу опорную формулу для вычисления статического момента точки массой m относительно точки или оси M=mr, где r – расстояние от массы до оси или точки. Это означает, что, если объект имеет размеры , соизмеримые расстоянием от его до оси, то нужны дополнительные вычисления.
Пусть дана плоская дуга y=f(x), непрерывная на [a;b] и однородная. Требуется вычислить статический момент этой линии относительно оси Ох. Т.к. размеры дуги (массы) соизмеримы с расстоянием от точек дуги до оси

Ох, то разобьем дугу на достаточно малые участки х с таким расчетом, чтобы эти участки можно было считать точками (расстояние от всех точек участка разбиения до оси Ох было практически постоянно). Тогда можно вычислить приближенное значение статического момента участка разбиения относительно оси Ох (вклад выделенной массы участка дуги в общий
статический момент всей дуги) Мох= l ρ r= ρ 1+( f '(x))2 r dx. Т.к. r=y, то
получаем Мох= ρ 1+( f '(x))2 f(x)dx. |
После суммирования и перехода к |
|
пределу получаем Mох= ∫b |
ρ 1+( f '(x))2 |
f(x)dx. |
a |
|
|
По аналогичной схеме решают и другие задачи.
3.Криволинейные интегралы
На основании механизмов, разработанных в разделе “Определенный интеграл”, решены задачи и получены новые типы интегралов , сводящихся к определенным.
3.1.Криволинейные интегралы 1-го года
Задача, приводящая к криволинейному интегралу 1-го рода. Вычислить массу неоднородной нити (дуги кривой, троса, провода, каната).
Решение. Поступаем так, как делали при решении задач с определенным интегралом. Делим дугу на достаточно малые участки, чтобы можно было приближенно считать плотность материала дуги на всем участке разбиения приближенно постоянной. Находим массу этого участка по формуле ρ V. В данном случае плотность ρ = ρ (М) , где М взята на участке
разбиения; V= |
l, |
т.е. роль объема выполнит длина участка (о размерности |
речи не идет |
– |
главное существо дела). Тогда m= ρ (М) l. После |
суммирования всех частичных масс и перехода к пределу, когда размеры максимального участка разбиения стремится к нулю, а число участков к бесконечности, получим массу всей дуги.
Пусть задана дуга непрерывная гладкая АВ и в каждой точке этой дуги задана функция f(M). Разобьем эту дугу точками на достаточно малые участки l. На каждом участке выберем точку М . Составим и вычислим
n
сумму∑f (M k ) lk . Назовем эту сумму интегральной. Подсчитаем предел этой
k =1
суммы при условии, что количество частей разбиения стремится к бесконечности, а длина максимального участка разбиения к нулю.
n
Опр. Если существует lim ∑f (M k ) lk независимо от способа
n→∞ k =1
разбиения дуги АВ на участки и выбора точек М на участках разбиения, то это предел назовем криволинейным интегралом первого рода (КРИ-1) и
обозначим ∫ f (M )dl .
AB
Из определения КРИ-1 вытекает, что для него справедливы : теорема существования и основные свойства , аналогичные свойствам определенного
интеграла. Из этих свойств не будет работать только одно – в котором идет речь о смене знака интеграла при смене направления интегрирования.
|
Для вычисления КРИ-1 |
используют приемы сведения его к |
||||
определенному интегралу. Рассмотрим несколько таких случаев. |
|
|||||
|
Пусть дуга АВ задана параметрически : x=x(t) ; y=y(t) ; z=z(t) . Тогда |
|||||
для |
достаточно |
малого |
участка |
l |
справедливо |
равенство |
l= |
( x)2 +( y)2 +( |
z)2 , т.к. l |
в этом |
случае |
можно рассматривать как |
|
диагональ прямоугольного параллелепипеда. Т.к. приращения можно
заменить |
дифференциалами, |
то |
получаем |
l= ( x)2 +( |
y)2 +( z)2 =dl= (dx)2 +(dy)2 +(dz)2 = |
(x't dt)2 +( y't dt)2 + (z't dt)2 = |
|
(x't )2 +( y't )2 +(z't )2 dt. И после подстановки под знак интеграла получаем формулу для его вычисления
|
tB |
∫ f (M )dl = ∫ f(x(t),y(t),z(t)) (x't )2 + ( y't )2 +(z't )2 dt, где tA и tBB значения |
|
AB |
tA |
параметра t |
для точек А и В. |
Для плоской дуги АВ , заданной параметрически , выведенная формула |
|
остается справедливой, но содержит на одну компоненту меньше – отсутствует z(t).
Если же плоская дуга АВ задана явно y=f(x), то все рассуждения остаются в силе и мы получим несколько иное выражение, которое встречалось уже при вычислении длины дуги определенным интегралом
∫ |
xB |
f (M )dl = ∫ f(x,y(х)) 1+( f '(x))2 dt. |
|
AB |
xA |
3.2. Криволинейные интегралы 2-го года
Задача. Вычислите работу переменной силы на криволинейном участке пути АВ.
Решение. Ранее мы уже решали задачи такого типа : в векторной алгебре вычисляли работу постоянной по величине и направлению силы на прямолинейном участке пути; в приложениях определенного интеграла вычисляли работу переменной по величине и постоянной по направлению силы на прямолинейном участке пути. Теперь пришла очередь решать задачу общего вида – сила переменная (и по величине, и по направлению) и путь криволинейный.
Разобьем дугу на достаточно малые участки, чтобы можно было приближенно считать участок разбиения l прямолинейным (что уже неоднократно делали) и чтобы на каждом участке разбиения можно было
→
приближенно считать действующую силу F постоянной по величине и направлению. В этом случае можно приближенно вычислить работу А
→ |
→ |
→ |
силы F по перемещению точки на пути l по формуле |
А= F |
l как это |
мы делали в векторной алгебре. После суммирования всех частичных работ и

перехода к пределу, когда максимальная длина участка разбиения стремится к нулю, а число участков – к бесконечности, мы получим искомую работу.
Пусть сила в пространстве имеется гладкая непрерывная кривая (дуга)
→ → |
|
АВ и в каждой точке М этой дуги задано поле F = F (М). Разобьем кривую |
|
АВ точками на отдельные достаточно малые участки |
lк с таким расчетом, |
чтобы на каждом участке разбиения можно было |
считать величину и |
→ |
|
|
направление F постоянными. На каждом участке разбиения выберем точку |
||
n |
→ |
→ |
Мк . Составим и вычислим сумму ∑F (M k ) |
lk . Назовем ее интегральной. |
|
k =1 |
|
|
n |
→ |
→ |
Вычислим предел этой суммы lim ∑F (M k ) |
lk . |
|
n→∞ k =1 |
|
|
Опр. Если указанный предел не зависит от способа разбиения дуги АВ на участки и выбора точки Мк на каждом участке разбиения, а зависит только
→
от длины дуги АВ и поля F , то этот предел назовем криволинейным
интегралом 2-го рода (по координатам) и обозначим символом ∫ |
→ → |
F dl . |
|
AB |
|
→
Комментарий. Ввиду того, что поле F можно записать по разному, так
→
же как и вектор dl , то можно получить другие символы для КРИ-2. Так, известно, что , если в пространстве введена декартова система координат, то
|
→ |
→ |
|
→ |
→ |
|
→ |
можно записатьF |
= F (М)=P(x,y,z) |
i +Q(x,y,z) j + R(x,y,z) k = |
|||||
|
|
|
|
→ |
|
|
|
( P(x,y,z) |
;Q(x,y,z) |
;R(x,y,z) ) |
, т.к |
F - это просто вектор (с точки зрения |
|||
|
|
|
|
→ |
→ |
→ |
→ |
векторной алгебры). Аналогично |
dl = dx |
i +dy |
j +dz |
k =(dx;dy;dz). После |
|||
чего мы получим несколько иные символы для КРИ-2 |
|
||||||
→ → |
→ |
→ |
|
|
|
|
|
∫ F dl |
= ∫ F (М) dl = ∫ |
P(x,y,z)dx+ |
Q(x,y,z)dy+ |
R(x,y,z)dz, т.к. под |
|||
AB |
AB |
AB |
|
|
|
|
|
знаком КРИ-2 было записано скалярное произведение двух векторов. При этом не принято (хотя и не запрещается) выражение P(x,y,z)dx+ Q(x,y,z)dy+ R(x,y,z)dz под знаком интеграла забирать в скобки. Из такой записи КРИ-2 следует его название в некоторых книгах – криволинейный интеграл по координатам.
Из определения КРИ-2 следует его интерпретация как работы по перемещению точки в поле силы по криволинейной траектории.
Если траектория (дуга, путь) замкнута, то говорят и о циркуляции
→
векторного поля F по замкнутому контуру . В этом случае для КРИ-2 используют специальный символ
∫ |
→ |
→ |
F dl = ∫ P(x,y,z)dx+ Q(x,y,z)dy+ R(x,y,z)dz. |
||
L L
Теорема существования. Если P(x,y,z), Q(x,y,z), R(x,y,z) непрерыны в каждой точке гладкой и кусочно непрерывной дуги АВ, то КРИ-2 существует.
Справедливы основные свойства , аналогичные свойствам определенного интеграла. Отметим одно важное – при смене направления движения по дуге АВ КРИ-2 меняет знак.
При вычислении КРИ-2 используют уже известные приемы сведения его к определенному интегралу.
Пусть дуга АВ плоская и задана явно y=f(x). Тогда естественно и поле
→ |
|
|
→ |
→ |
→ |
→ |
→ |
→ |
|
F плоское |
F = P(x,y) i +Q(x,y) |
j |
и dl = dx i +dy |
j . Тогда КРИ-2 будет |
|||||
приведен к определенному по формуле |
|
|
|||||||
∫ |
→ → |
и |
|
|
|
|
и |
|
|
F dl = ∫ |
(P(x,f(x))dx+ Q(x,f(x))f’(x)dx)= ∫ |
(P(x,f(x))+ Q(x,f(x))f’(x))dx. |
|||||||
AB |
|
а |
|
|
|
|
а |
|
|
|
Пусть дуга АВ плоская и задана параметрически x=x(t) ; y=y(t). Тогда |
||||||||
для вычисления КРИ-2 получаем формулу |
|
|
|||||||
|
∫ |
→ |
→ |
tB |
|
|
|
|
|
|
F dl = ∫ |
(P(x(t),y(t)) y’t(t)+ |
Q(x(t),y(t))y’t(t))dt. Такая же формула, |
||||||
|
AB |
|
|
tA |
|
|
|
|
|
только с большим числом слагаемых будет получена, если АВ пространственная и задана параметрически.
Если интегрирование ведут по контуру, то договариваются движение по контуру считать выполненным в положительном направлении, если при движении по контуру, точки области, расположенной внутри контура остаются слева от движущегося. Такое направление движения считается согласовнным.
В приложениях важно связь интеграла по контуру с тем, что делается внутри контура (в лесном хозяйстве, охотоведении, топографии, электротехнике, нефтегазоразведке). В качестве примера приведем формулу для вычисления площади S, охватываемой контуром L.
Пусть дана односвязная область D с границей Г. Тогда площадь области можно подсчитать, как известно, определенным интегралом по
формуле S= ∫и f2(x)dx- ∫и f1(x)dx , где у= f2(x) – это та часть контура L,
аа
которая ограничивает область сверху (см.Рис 12.1); а у= f1(x) – это та часть контура L, которая ограничивает область снизу.
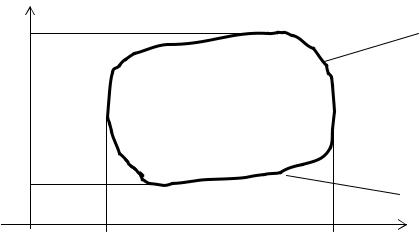
у |
|
|
d |
N |
y=f2(х) |
A
|
|
|
B |
|
c |
K |
|
|
y=f1(x) |
|
|
b |
||
|
а |
|
х |
|
Рис 12.1. К вычислению площади по КРИ-2. |
|
|||
Но ∫и |
f1(x)dx= ∫ ydx , а |
∫и |
f2(x)dx= ∫ ydx |
, т.е. представлены |
а |
AКB |
а |
ANB |
|
криволинейными интегралами по соответствующим кривым. Поэтому
искомая площадь будет выражена так S= ∫и |
f2(x)dx- ∫и |
f1(x)dx = ∫ |
ydx - ∫ ydx |
а |
а |
ANB |
AКB |
. Но ∫ ydx взят против согласованного направления движения по контуру Г.
ANB
А потому перед ним следует сменить знак. И тогда получим S= - ∫ ydx -
BNA
∫ ydx= =-  ∫ ydx. Проделаем такую же работу после проектирования на ось
∫ ydx. Проделаем такую же работу после проектирования на ось
AКB |
Г |
Оу и получим еще одну формулу для вычисления площади области S=  ∫ хdу. Просуммируем обе формулы площади и получим окончательно
∫ хdу. Просуммируем обе формулы площади и получим окончательно
Г
S=  ∫ хdу – ydx. На этой формуле и основана работа планиметра –
∫ хdу – ydx. На этой формуле и основана работа планиметра –
Г
прибора, после установки на шкале которого масштаба, достаточно прокатить роликом считывающего приспособления по границе области и на счетчике можно получить площадь этой области. Такую же работу делает охотник, прослеживая по границе леса количество входящих и выходящих из леса следов. После обхода он указывает количество обитающего в лесу зверя.
3.3.Независимость КРИ-2 от пути интегрирования
Не следует воспринимать заголовок как гарантию абсолютной независимости КРИ-2 от пути интегрирования. Дело обстоит несколько иначе.
Пусть некоторый КРИ-2 вида ∫ P(x,y)dx+ Q(x,y)dy мы вычислили по
AB
дуге кривой АКВ. Затем подсчитали этот же интеграл , но уже по пути ANB. Если при этом результаты окажутся одинаковыми, то говорят, что данный
∫ P(x,y)dx+ Q(x,y)dy не зависит от пути интегрирования(см.Рис 12.1).
AB
Однако мы продолжим рассуждать далее и обнаружим, что в этом случае

 ∫ P(x,y)dx+ Q(x,y)dy = 0 ! И это вполне естественно. Таким образом,
∫ P(x,y)dx+ Q(x,y)dy = 0 ! И это вполне естественно. Таким образом,
Г
независимость КРИ-2 от пути интегрирования эквивалентно понятию равенства нулю того же КРИ-2 , но ! уже по замкнутому контуру, проходящему через те же две указанные в самом начале точки.
Теорема(о независимости КРИ-2 от пути интегрирования). Пусть в D, содержащей гладкую кривую АВ,не имеющей точек самопересечения, заданы непрерывные и имеющие непрерывные частные производные
функции P(x,y) и Q(x,y). Тогда для независимости ∫ P(x,y)dx+Q(x,y)dy
AB
необходимо и достаточно, чтобы во всех точках области выполнялось условие ддQx = ддPy .
Доказательство можно найти в разделе “Теория поля - Формула Грина”.
4.Кратные интегралы.
На основании механизмов, разработанных в разделе “Определенный интеграл”, решены задачи и получены новые типы интегралов , сводящихся к определенным.
4.1.Задачи, приводящие к кратным интегралам.
Задача 1. Вычислите объем цилиндроида. Цилиндроидом называют пространственное тело, ограниченное снизу областью D с границей Г, сбоку цилиндрической поверхностью с образующей, перпендикулярной плоскости области D, и направляющей в виде границы Г и сверху поверхностью z=f(М)>0 , где z=f(М) –определена в каждой точке D.
Задача 2. Вычислить массу неоднородного тела, ограниченного поверхностью S , плотность распределения массы задана величиной
ρ = ρ(M ) .
Решение этих задач выполним по одному алгоритму. Начнем с задачи 1. Т.к. нет рабочей формулы для вычисления объема цилиндроида, то разобьем D на достаточно малые участки площадью οk . Тогда над каждым
таким участком расположится некоторый объем , который можно считать приближенно имеющим постоянную высоту f(Mk). И величину этого объема можно подсчитать Vk ≈ f(Mk) οk . Если теперь просуммировать все
частичные объемы и вычислить предел полученной суммы , когда размеры частей οk уменьшаются, а число их растет неограниченно, то мы вычислим
n
объем цилиндроида V=lim ∑f (M k ) οk .
n→∞ k =1
Аналогичные рассуждения приведут нас к ответу во второй задаче
|
n |
m=lim ∑ρ(M k ) Vk , где разбиении произведено на части Vk , т.к. тело |
|
n→∞ |
k =1 |
неоднородно и с таким расчетом, чтобы при достаточно малых частях разбиения плотность материала можно было считать приближенно постоянной.
