
- •Рабочая программа
- •Пояснительная записка
- •Тематический план
- •Литература
- •Конспект лекций
- •Понятие множества и операции над множествами
- •Числовые множества
- •Абсолютная величина действительного числа. Окрестность точки
- •Функция одной независимой переменной
- •Основные элементарные функции. Сложная функция
- •Предел и непрерывность функции
- •Дифференциальное исчисление функции одной независимой переменной
- •Приложения производной
- •Правило Лопиталя
- •Исследование функций и построение графиков
- •Неопределенный интеграл
- •Метод замены переменной (метод подстановки)
- •Интегрирование по частям
- •Интегрирование простейших рациональных дробей
- •Определенный интеграл и его приложения
- •Дифференциальные уравнения
- •Методы интегрирования дифференциальных уравнений первого порядка
- •Дифференциальные уравнения второго порядка, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Контроль знаний
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольные вопросы к зачету
- •Контрольные вопросы к экзамену
- •Глоссарий

2.Конспект лекций
2.1.Понятие множества и операции над множествами
Вматематике все понятия делятся на первичные и определяемые через первичные. Первичные понятия не могут быть определены и, как правило, разъясняются на примерах.
Основным первичным понятием математики является понятие множество. Под множеством понимается совокупность (семейство, набор, объединение, система) некоторых объектов. Примером множеств может служить множество зрителей в театре, множество студентов в группе, множество яблок на дереве и т.д. Множество может содержать конечное или бесконечное число объектов. Объекты, составляющие множество, называются его элементами, или точками.
Множества обозначаются прописными буквами латинского алфавита, а их элементы – строчными. Если а есть элемент множества А, то используется за-
пись а А. Если b не является элементом множества А, то пишут b А. Множество, не содержащее ни одного элемента, называется пустым и обо-
значается символом .
Если множество B состоит из части элементов множества А или совпадает с ним, то множество В называется подмножеством множества А и обозначается В А. Например, А – множество всех студентов вуза, а В – множество студен- тов-первокурсников этого вуза, то В есть подмножество А, т.е. В А.
Два множества равны, если они состоят из одних и тех же элементов А=В. Объединением двух множеств А и В называется множество С, состоящее из
всех элементов, входящих как во множество А, так и во множество В. Обозначение С=А В, геометрически – вся заштрихованная часть на рис. 1.
А В |
= С |
Рис. 2.1. Объединения множеств
Примеры объединения множеств.
1.Пусть имеются два сплава. Один сплав содержит железо, углерод, ванадий, марганец, а второй – железо, углерод, хром, никель. В каждый сплав входят 4 элемента, но если мы их сплавим вместе, то в новый сплав войдут только 6 элементов: железо, углерод, ванадий, марганец, хром и никель.
Для конечных множеств число элементов суммы может оказаться меньше, чем сумма чисел элементов слагаемых.
2.Пусть первое множество состоит из различных букв русского алфавита, входящих в первую строку «Евгения Онегина», а второе – из различных букв, входящих во вторую строку этого романа; тогда первое множество имеет 18
элементов: м, о, й, д, я, с, а, ы, х, ч, е, т, н, п, р, в, и, л, а второе – 13: к, о, г, д, а,
н, е, в, ш, у, т, з, м. Объединение этих множеств дает 23 элемента: м, о, й, д, я, с,
а, ы, х, ч, е, т, н, п, р, в, и, л, к, г, ш, у, з.
9
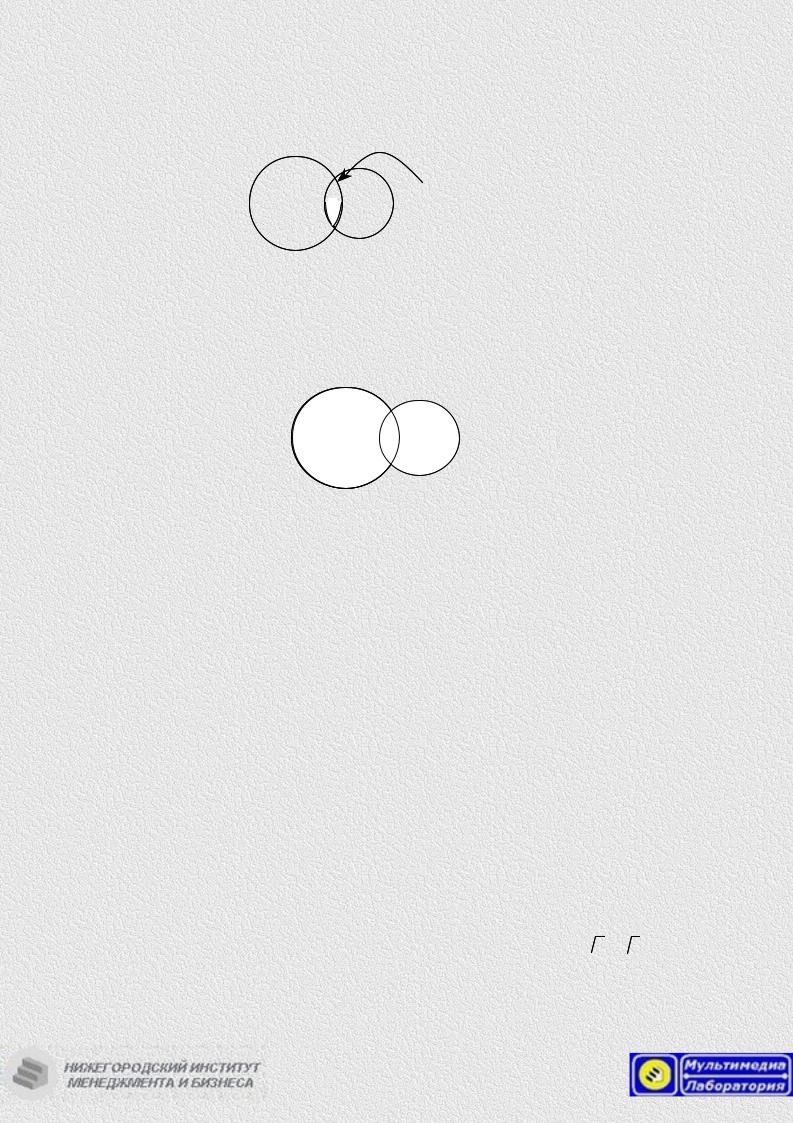
Пересечением двух множеств А и В называется множество D, состоящее из всех элементов, одновременно принадлежащих каждому из данных множеств А и В. Обозначение D=А∩В, заштрихованная область на рис. 2.
А  В D
В D
Рис. 2.2. Пересечения множеств
Разностью множеств А и В называется множество Е, состоящее из всех элементов множества А, которые не принадлежат множеству В. Обозначение Е=А\В. Е – заштрихованная область на рис. 3.
В
Рис. 2.3. Разность множеств
Пример
Даны множества А={1, 3, 6, 8}, В={2, 4, 6, 8}. Найти объединение, пересечение и разность множеств А и В.
∆ Объединение |
А В = {1, 2, 3, 4, 6, 8} |
Пересечение |
А∩В = {6, 8} |
Разность |
А\В = {1, 3} |
2.2. Числовые множества
Целые положительные числа 1, 2, 3,… n образуют множество натуральных чисел N. Присоединяя к натуральным числам все целые отрицательные числа и нуль, получим множество целых чисел Z.
Все целые числа вместе с дробными числами образуют множество рациональных чисел Q. Рациональным называется число вида p/q, где p и q – целые числа, и является либо целым, либо представляет собой конечную или периодическую десятичную дробь: 1/3=0,333…
Иррациональным числом называется бесконечная непериодическая десятичная дробь (положительная или отрицательная). Например:  2 ,
2 ,  3 , π, log23, sin1°. Иррациональные числа образуют множество I. Все рациональные и ирра-
3 , π, log23, sin1°. Иррациональные числа образуют множество I. Все рациональные и ирра-
циональные числа образуют множество действительных чисел R.
Очевидно, что N Z Q R, I R, R=Q I.
10
Геометрически множество действительных чисел R изображается прямой, на которой выбрано начало отсчета, положительное направление и единица масштаба. Эта прямая называется числовой осью. Между множеством действительных чисел и точками числовой оси существует взаимооднозначное соответствие, то есть каждому действительному числу соответствует определенная точка числовой прямой, и наоборот, каждой точке прямой – определенное действительное число.
Пусть а и b – два числа, причем а<b. Множество чисел х, удовлетворяющих неравенствам а≤х≤b, называется отрезком и обозначается [а, b].
Множество чисел х, удовлетворяющих неравенствам а<х<b, или а<х<∞, или -∞<х<b, или -∞<х<∞, называется интервалом и обозначается (а, b), или (а, ∞), или (-∞, b), или (-∞, ∞) соответственно.
Множество чисел х, удовлетворяющих неравенствам а≤х<b, или а<х≤b, или а≤х<∞, или -∞<х≤b, называется полуинтервалом и обозначается [а, b), или (а, b], или [а, ∞), или (-∞, b] соответственно.
Все эти множества называют промежутками. Интервал (а, b) не содержит ни наибольшего, ни наименьшего числа, с, в то время как в отрезке [а, b] такими элементами являются соответственно b и а.
2.3. Абсолютная величина действительного числа. Окрестность точки
Абсолютной величиной (или модулем) числа х называется само число х, если х ≥ 0, или число – х, если х < 0.
Абсолютная величина числа х обозначается символом x . Таким образом:
x |
|
= |
х, |
если |
x ≥ 0 |
|
|||||
|
|
|
− х, |
если |
x < 0 |
|
|
|
Например: 7 = 7 ; −7 = −(−7) = 7 ; 0 = 0 .
Свойства модуля
1. Модуль любого действительного числа x есть неотрицательное число, т.е. x ≥ 0 .
2.Для любых действительных х и у: xy = x × y .
3.Для любого действительного х и у≠0: xy = xy .
4. |
Неравенство |
|
|
x |
|
≤ a , |
где |
а>0, |
равносильно |
неравенствам |
− a ≤ x ≤ a |
или |
||
|
|
|
||||||||||||
x [−a, a] . |
|
|
|
|
> b , |
где |
|
равносильно |
неравенствам |
|
или |
|||
5. |
Неравенство |
|
x |
|
b > 0 |
x > b, x < −b |
||||||||
|
|
|||||||||||||
x (−∞,−b) (b, ∞) .
6.x − y = y − x .
7.Модуль суммы не превосходит сумму модулей, то есть x + y ≤ x + y .
8.x − y ≤ x − y ≤ x + y .
11

Абсолютная величина разности двух чисел x − a означает расстояние между точками х и а числовой прямой как для случая х<а, так и х>а.
|
|
|
|
|
|
|
|
x − a |
|
|
|
|
|
|
х>a |
|
|
|
x − a |
|
|
|
|
|
|
|
|
|||||||||
|
х<a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
а |
|
|
|
|
|
|
х |
|
|
|
|
|||||||
|
|
Рис. 2.4. Абсолютная величина разности двух чисел |
|
x − a |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
Поэтому решениями неравенства |
|
x − a |
|
< ε (ε > 0) |
будут точки х интервала |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
(a −ε, a +ε) , удовлетворяющие неравенствам a −ε < x < a +ε .
εε
a-ε a a +ε
Рис. 2.5. Интервал, содержащий точку а
Всякий интервал, содержащий точку а, называется окрестностью точки а. Интервал (a −ε, a +ε) называется ε – окрестностью точки а.
2.4. Функция одной независимой переменной
Пусть даны два непустых множества X и Y. Если каждому элементу х из множества X по определенному правилу ставится в соответствие один и только один элемент у из Y, то говорят, что на множестве X задана функция со множеством значений Y. Множество X называется областью определения функции, а множество Y, состоящее из всех чисел вида y=f(x), – множеством значений функции. Буква f (иногда пишут ϕ) характеризует то правило, по которому получается значение у, соответствующее заданному аргументу х.
Существует несколько способов задания функции:
1)аналитический способ, если функция задана формулой;
2)табличный способ;
3)графический способ;
4)словесный способ, если функция описывается правилом ее составления, например, функция Дирихле: f(x) = 1, если х – рационально; f(x)=0, если х – иррационально.
Основные свойства функций
1.Четность и нечетность
Если область определения функции f(x) есть множество, симметричное относительно начала координат, то y=f(x) называется четной, если для любых х из области определения f(–x)= f(x), и нечетной, если f(–x)=–f(x). В противном случае функция y=f(x) называется функцией общего вида.
График четной функции симметричен относительно оси ординат Оу, график нечетной функции симметричен относительно начала координат.
12

Примеры
1. Доказать, что функция f (x) = |
x2 |
является четной. |
|
x2 − 4 |
|||
|
|
∆ Будем обозначать область определения через D(f). Так как для нашей |
|||||
функции |
D(f ) = (−∞,−2) |
(−2,2) (2,∞) – симметричное относительно точки |
|||
О множество и |
|
|
|
|
|
f (− x)= |
(− x)2 |
= |
x2 |
= f (x), то f(x) – четная функция. |
|
|
x2 − 4 |
||||
|
(− x)2 − 4 |
|
|
||
2. Доказать, что функция f (x) = x5 − x3 + x – нечетная. |
|||||
∆ D(f )= (−∞, ∞); |
f (− x)= (− x)5 |
−(− x)3 + (− x)= −(x5 − x3 + x)= − f (x). Следователь- |
|||
но, функция нечетная. |
|
f (x)= x4 + x2 , определенная на множестве |
|||
3. Является |
ли |
функция |
|||
D(f )= [− 2;10), четной.
∆ Эта функция не является ни четной, ни нечетной, так как ее область определения не симметрична относительно начала координат. Хотя формально f(–x)= f(x).
2. Монотонность
Функция y = f (x) называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
Интервалы возрастания и убывания называются интервалами монотонности функции, а функция в этих интервалах – монотонной.
Например, функция y = x2 при x (−∞,0] убывает и при x [0, ∞) возрастает.
3. Ограниченность
Функция f(x) называется ограниченной на промежутке Х, если существует такое положительное число М>0, что f (x) ≤ M для любого x X .
Например, функция y = cos x ограничена на всей числовой оси, так как cos x ≤1 для любого x R .
4. Периодичность
Функция f(x) называется периодической, если существует число T ≠ 0 такое, что для любого значения х из области определения функции выполняется равенство f (x +T )= f (x). Число Т называется периодом функции. Например, пе-
риодом функций sin x и cos x является число T = 2π : sin(x + 2π)= sin x , cos(x + 2π )= cos x , а периодом функций tg x и сtg x – число T =π .
Если Т – период функции, то ее периодом будет также и число kT, где k – любое целое число ( k = ±1, ± 2,... )
Если функции f(x) и g(x) – периодические с периодом Т1 и Т2 соответственно, то периодом их суммы, произведения, разности и частного является число Т, кратное Т1 и Т2.
13
