§4. Ранг матрицы

В этом параграфе мы познакомимся с новым понятием ранга матрицы, которое понадобится при решении систем линейных уравнений (§6) и нахождении базиса системы векторов (§7).

Определение 1.4.Минором k-го порядкапроизвольной матрицыАназывается определитель, составленный из элементов матрицы, расположенных на пересечении каких-либоkстрок иkстолбцов (элементы выписаны в том же порядке, в каком они входят в матрицу А).

Например, в матрице 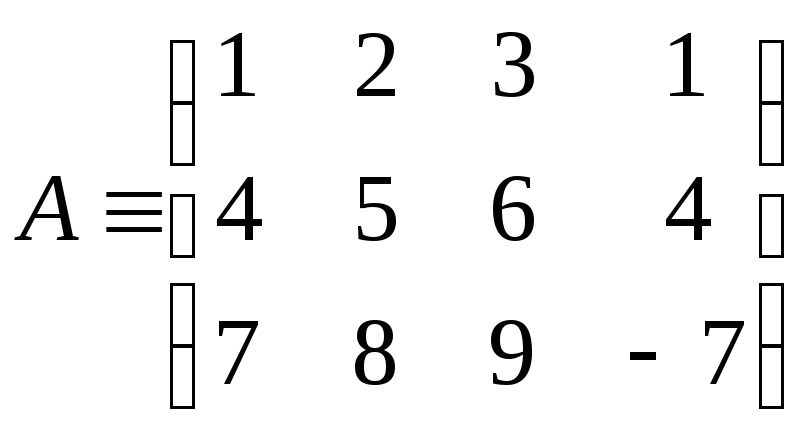можно указать такие миноры:

• 1-го порядка ;

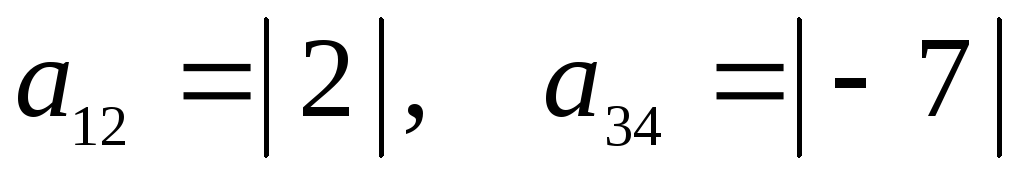• 2-го порядка ;

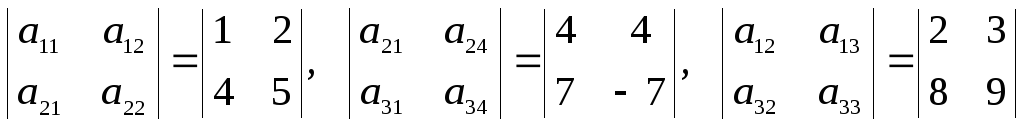• 3-го порядка .

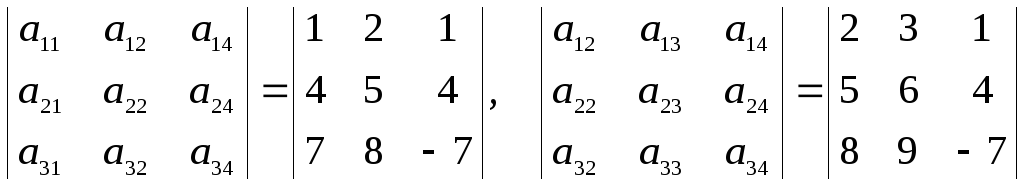Определение 2.4.Рангом матрицыА(rangА) называется наивысший порядок отличных от нуля миноров этой матрицы.

□

Найдем ранг матрицы . Ясно, чтоrangА=1.

Действительно, любой из миноров 2-го порядка равен нулю, и существует хотя бы один минор 1-го порядка | 3 | = 3, не равный нулю.

■

Определение 3.4.ПустьrangА=r. Любой ненулевой минорr-го порядка матрицыАназываетсябазисным минором. Строки и столбцы матрицы, участвующие в образовании базисного минора, также называютсябазисными.

Заметим, что в общем случае у матрицы может быть несколько базисных миноров.

Свойства ранга матрицы:

1. если матрица имеет размеры mn, то ранг ее будет не больше минимального из чиселmиn : rangА ≤min(m,n);

2. rangА= 0 тогда и только тогда, когдаА– нулевая матрица;

3. если А– квадратная матрицаn-го порядка, тоrangА=nтогда и только тогда, когдаА– невырожденная матрица, т.е.detA≠ 0.

Разыскивать ранг матрицы, пользуясь определением, просто, если сама матрица небольших размеров. Задача значительно усложняется, если приходится вычислять миноры третьего порядка и выше. Для этих случаев существует более простой способ элементарных преобразований.

Предварительно определим некоторые понятия.

Элемент строки матрицы назовем крайним,если он отличен от нуля, а все элементы этой строки, находящиеся левее него, равны нулю.

Матрица называется ступенчатой, если крайний элемент каждой строки находится правее крайнего элемента предыдущей строки.

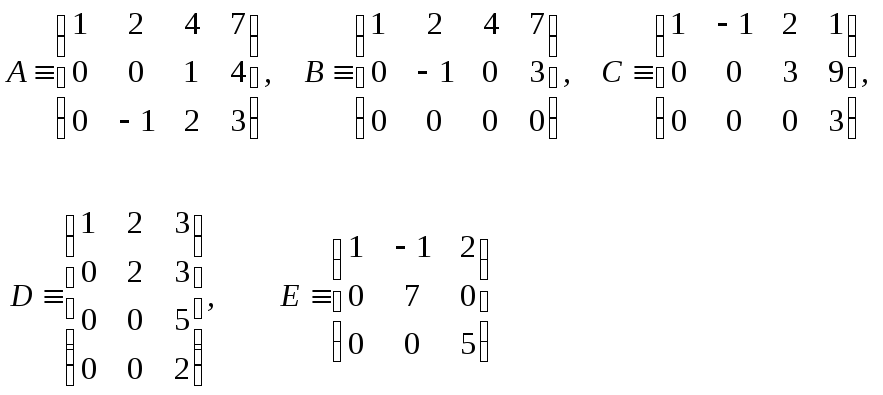
Среди перечисленных ниже матрицы В,С,Еявляются ступенчатыми, аА,Dступенчатыми не являются (чертой отмечены крайние элементы каждой строки).

Вспомним элементарные преобразования матрицы, описанные нами ранее в §3. Перечислим утверждения, опираясь на которые мы определим еще один метод вычисления ранга.

Теорема 1.Элементарные преобразования не меняют ранга матрицы.

Теорема 2. С помощью элементарных преобразований любую матрицу можно привести к ступенчатому виду.

Теорема 3.Ранг ступенчатой матрицы равен количеству ее ненулевых строк.

Отсюда следует алгоритм нахождения ранга матрицыметодом элементарных преобразований:

1. приводим матрицу к ступенчатому виду с помощью элементарных преобразований;

2. определяем ранг по количеству ненулевых строк полученной матрицы.

□

Найдем ранг матрицы .

Приведем матрицу Ак ступенчатому виду. Для удобства вычислений поменяем 1-ю и 2-ю строки местами, тогда крайний элемент 1-й строки станетa₁₁=10. Умножим элементы 1-й строки на (2) и (1), прибавим их соответственно к элементам 2-й и 3-й строк (см. обозначения), чтобы все элементы 1-го столбца, стоящие под элементомa₁₁, равнялись нулю.

В новой матрице крайний элемент 2-й строки a₂₂=30. Чтобы привести её к ступенчатому виду, необходимо сделать нулевым элемент 2-го столбца, стоящий под элементомa₂₂. Для этого умножим элементы 2-й строки на (2) и прибавим их к элементам 3-й строки.

Полученная ступенчатая матрица содержит две ненулевые строки, следовательно, rang А=2.

Любой ненулевой минор 2-го порядка полученной матрицы может быть базисным, например, .

■

Заметим, что, выполняя элементарные преобразования матрицы, мы последовательно манипулировали строками этой матрицы: находили некоторое число, умножали его на строку, затем результат складывали с другой строкой и т.д. Возникает вопрос: можно ли эти действия выразить некоторой формулой? Например, вместо слов «умножаем элементы второй строки на (2) и прибавляем их к элементам третьей строки» можно написать формулу2е₂+е₃, гдее₂ие₃– обозначения 2-й и 3-й строк.

Обозначая строки некоторыми буквами, мы приходим к понятию линейной комбинации. Оно позволит нам установить связь между понятиями «ранг матрицы» и «линейная зависимость (независимость) строк матрицы», что понадобится нам в §7.

Определение 4.4. Линейной комбинациейстрок (столбцов) матрицые₁,е₂, …,е_mназывается выражение вида

λ₁е₁+λ₂е₂+…+λ_mе_m,

где λ_i() – некоторые числа.

Определение 5.4.Строки (столбцы) матрицые₁,е₂, …,е_mназываютсялинейно зависимыми, если существуют такие числа λ₁, λ₂,…,λ_m, не равные одновременно нулю, что

λ₁е₁+λ₂е₂+…+λ_mе_m =,(1.4)

где = (0, 0,…,0) – нулевая строка (столбец).

Если же равенство (1.4) возможно лишь при λ₁ = λ₂ = … = λ_m = 0, то строки (столбцы) матрицы называютсялинейно независимыми.

□

Поясним на примере.

Строки матрицы

линейно зависимы, т.к. найдутся λ₁=0 и λ₂=5 (не равные одновременно нулю), что

0·(3, 2, 2) + 5·(0, 0, 0) = (0, 0, 0).

А строки матрицы

линейно независимы, т.к. линейная комбинация

λ₁·(1, 1, 1) + λ₂·(0, 1, 4) = (0, 0, 0) только при λ₁=λ₂=0.

■

Теорема о ранге матрицы.Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов.

В курсе алгебры важную роль играет следующая теорема. Базисные строки (столбцы) матрицы линейно независимы.

Следствие. Всякая строка (столбец) матрицы является линейной комбинацией ее базисных строк (столбцов).

□

Снова обратимся к примеру, где мы находили ранг матрицы

.

Обозначим строки матрицы е₁,е₂,е₃соответственно, т.е.

.

Полученная ступенчатая матрица

содержит две ненулевые строки.

Строки е₁,е₂,е₃матрицы являются линейно зависимыми, т.к.

–3е₁+2е₂е₃=

(проверьте справедливость этого равенства).

RangА=2, поэтому две строки будут линейно независимыми, например,е₁,е₂, а третья строка е₃будет линейной комбинацией этих двух:

–3е₁+2е₂е₃+е₃=+е₃;

+е₃=е₃,е₃+е₃=;

е₃= –3е₁+2е₂.

Здесь строки е₁ие₂могут служить базисными строками.

■