Курс лекций по линейной алгебре

Содержание

Предисловие 4

§2. Определители квадратных матриц 13

§3. Обратная матрица. Матричные уравнения 20

§4. Ранг матрицы 28

§5. Системы линейных алгебраических уравнений. Метод обратной матрицы и теорема Крамера 33

§6 Решение систем линейных уравнений общего вида. 41

Метод Гаусса 41

§7. N-мерный вектор и векторное пространство. Евклидово пространство 50

§8 Линейные операторы. Собственные векторы и собственные значения линейного оператора 57

Контрольные вопросы 65

Предисловие

Перед вами цикл лекций по линейной алгебре, предназначенный для студентов первого курса заочного отделения экономического факультета.

Целью преподавания данной дисциплины является создание у студента базы для освоения математических моделей и методов в экономике.

Задачей изучения дисциплины «Линейная алгебра» является формирование теоретических знаний, необходимых для изучения других математических дисциплин, и практических навыков в решении прикладных задач с применением аппарата линейной алгебры.

Линейная алгебра является основой при изучении теории вероятностей и математической статистики, численных методов, методов оптимизации, а также современных экономико-матема-тических методов.

Занятия по дисциплине состоят из потоковых лекций и групповых практических занятий. В лекциях излагаются основные понятия и теория построения математических конструкций, теоремы. Большинство теорем рассматриваются без доказательств, т.к. за то небольшое количество аудиторных часов, что отводится на лекции, просто невозможно изучить материал курса в полном объеме. На практических занятиях с помощью решения задач отрабатываются теоретические положения лекции.

Следует обратить особое внимание на то, что при заочном обучении большая часть учебной нагрузки приходится на самостоятельную работу студента. Поэтому в основе занятий по данной дисциплине лежит индивидуальная самостоятельная работа с персональной консультацией у преподавателя. Студент должен также понимать, что ограничиваться изучением только материала данного пособия недостаточно, и следует обращаться к учебной литературе, например, из списка, приведенного на стр. 56.

По завершении курса проводится домашняя контрольная работа, задания к которой можно найти в учебно-методическом пособии [8], и экзамен, состоящий из теоретической и практической частей.

Список обозначений:

□ ■ – начало и конец решения примера или задачи, соответственно;

З

– замечание;

У

– упражнение.

В рамку заключены формулы, которые важно помнить.

§1. Матрицы. Операции над ними

Многие характеристики окружающих нас явлений, процессов, объектов описываются числами, например, вес товара и его стоимость, температура тела и др. Это простыевеличины. А как описать стоимость всех товаров, стоящих на пяти полках по семь на каждой? Здесь уже одним числом не обойтись, а понадобится таблица, например, из пяти строк, причем каждая строка будет соответствовать полке, а число в строке будет сопоставляться со стоимостью товара, стоящего на соответствующем месте полки. Такая таблица – это тоже математический объект, в нем уже задействованынаборычисел. Поскольку такой объект может быть представлен как совокупность более простых, его называютструктурированным,структурированной величиной. В математике для таблицы используют специальный термин – матрица. Дадим формальное определение этому понятию.

Определение 1.1.Матрицейразмераmnназывается прямоугольная таблица чисел, содержащаяmстрок иnстолбцов:

.

Матрицу Аразмераmnобозначают так:А_mn.

Числа, составляющие матрицу, называются ее элементами.

Элемент матрицы, стоящий на пересечении строки с номером i(номера считаются сверху вниз) и столбца с номеромj(номера считаются слева направо), обозначаетсяa_ij .

Знак «≡» означает тождественное равенство.

Как упоминалось выше, матрицы отображают реальные объекты. Например, следующая таблица распределения ресурсов (в усл.ед.) по отраслям экономики

Ресурсы	Отрасли экономики
	промышленность	сельское хозяйство
Электроэнергия	5,3	4,1
Трудовые ресурсы	2,8	2,5
Водные ресурсы	4,8	5,7

может быть записана в компактной форме в виде матрицы:

,

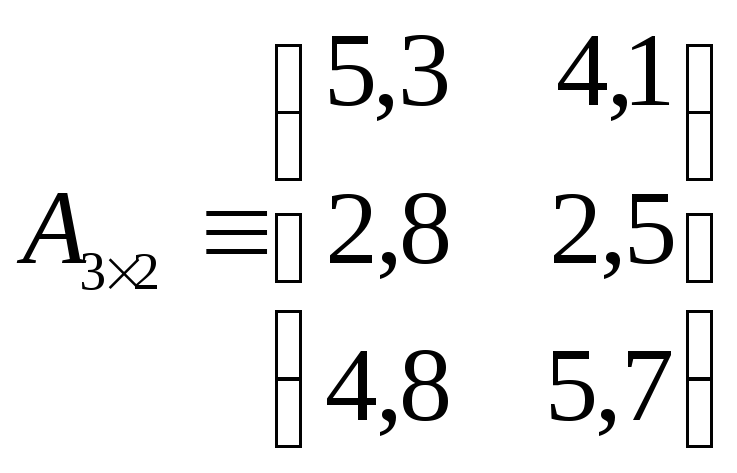где, например, элемент а₁₁=5,3 показывает, сколько электроэнергии потребляет промышленность.

Определение 2.1.Квадратной матрицейn-го порядка называется матрицаА_nn.

Определение 3.1. Главной диагональюквадратной матрицы называется совокупность элементова₁₁,а₂₂,а₃₃, … ,а_nn.

Квадратную матрицу назовем диагональной, если все ее элементыa_ij, лежащие вне главной диагонали (i≠j), равны нулю.

Определение 4.1.Единичной матрицейЕn-го порядка называется диагональная матрица, у которой каждый элементa_ii, находящийся на главной диагонали, равен единице.

Например, – единичная матрица 2-го порядка.

Определение 5.1. Нулевой матрицейназывается матрица, все элементы которой равны нулю.

Например, – нулевая матрица.

Определение 6.1.Матрицей-столбцом или матрицей-строкойназывается матрица, содержащая один столбец или одну строку соответственно:

– матрица-столбец;– матрица-строка.

Определение 7.1.МатрицыАиВодинакового размера называютсяравными, если каждый элемент матрицыАравен соответствующему элементу матрицыВ :

А≡В,a_ij≡b_ij, где , .

Запись,означает, что номераiизменяются от 1 доm, а номераj– от 1 до n.

Над матрицами определен ряд операций. Рассмотрим их.

Определение 8.1.Суммой матрицАиВразмераmnназывается матрицаСтого же размера, каждый элемент которой равен сумме соответствующих элементов матрицАиВ :

С≡А +В, с_ij≡a_ij +b_ij, где,.

□

.

■

Определение 9.1. Произведением матрицыАна числоλназывается матрицаС, каждый элемент которой равен произведению соответствующего элемента матрицыАна числоλ :

С≡λ∙А≡А∙λ, с_ij≡λ∙а_ij , где,.

□

.

■

Разность двух матриц одинакового размера определяется через две предыдущие операции:

А–В≡А + (–1)∙В.

Определение 10.1. Произведением матрицАразмераmkи В размераknназывается матрицаСразмераmn, каждый элементс_ijкоторой равен сумме произведений элементовi-й строки матрицыАна соответствующие элементыj-го столбца матрицыВ:

С _{m  n}≡А _{m  k} ´В _{k  n},

, где,.

Получение элемента с_ij схематично изображается так: чтобы найти элементс_ij, нужно “приложить”i-ю строку матрицыАкj-му столбцу матрицыВ, перемножить соответствующие элементы и полученные произведения сложить.

Обратим особое внимание на следующие моменты.

1. Умножение матрицы А на матрицу В определено только тогда, когда число столбцов первой матрицы равно числу строк второй.

□

Найдем произведение матриц и.

Число столбцов в матрице А совпадает с числом строк в матрице В, значит, произведение существует. Определим размер матрицы–произведения.

■

Заметим, что произведение ненулевых матриц оказалось равным нулевой матрице (в отличие от действительных чисел, когда произведение ненулевых сомножителей равным нулю быть не может).

2. Если произведение А´В матриц определено, то нельзя сказать, что существует также и произведение В´А. Даже если определены оба произведения А´В и В´А, то в общем случае они не равны.

□

Чтобы продемонстрировать справедливость этого утверждения, перемножим, например, вектор-строку Аи вектор-столбецВв разном порядке, и покажем, что А´ВВ´А.

Число столбцов в матрице А совпадает с числом строк в матрице В (и наоборот), значит, произведения существуют. Определим размер матриц-произведений.

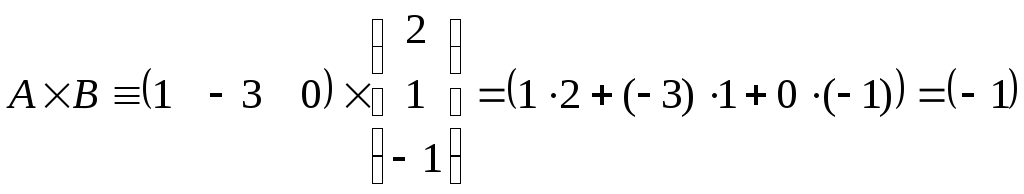
Убедились, что матрица А´В – размера 11, а В´А– размера 33.

■

Иногда удобно при вычислениях использовать свойства операций над матрицами. Некоторые из них аналогичны операциям над действительными числами, а некоторые – специфические. Перечислим их.

Пусть А,В,С– матрицы, λ, μ – некоторые числа.

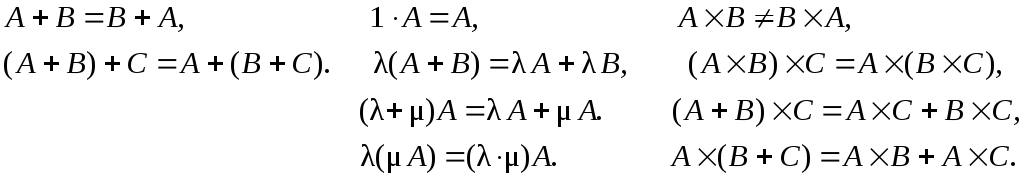
Для любого действительного числааединица – число, обладающее особыми свойствами:. Среди квадратных матриц аналогичным свойством обладает единичная матрица:.

Для матрицАиЕсамостоятельно вычислить произведенияА´ЕиЕ´А. Убедиться в справедливости замечания, если:

.

Определение 11.1.Транспонированиемназывается замена строк матрицы на её столбцы с сохранением их порядка.

Исходная матрица А_mnи транспонированная матрицаА^Т_nmимеют вид:

,

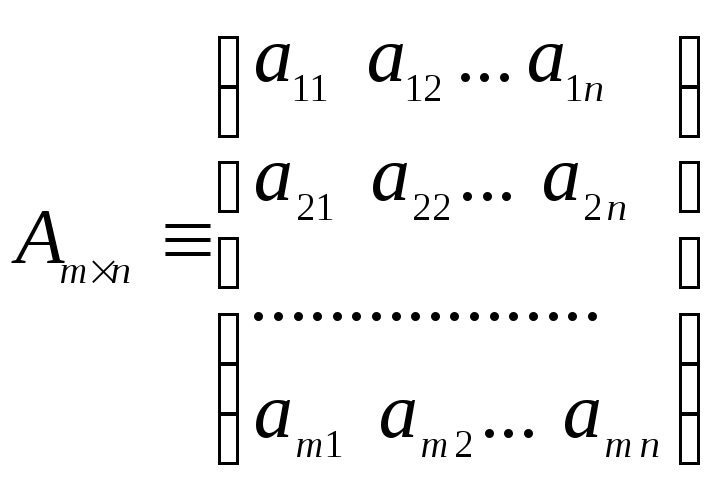Например, .

Свойства операции транспонирования:

Определение 12.1.Возвести матрицуАв степеньn– значит умножить её на себяnраз, т.е..

Возведение в степень 1, 2, 3,… определено только для квадратных матриц.

□

.

■