Лабораторная работа №3 Кратчайшие пути между всеми парами вершин графа.

Составить программу нахождения кратчайшего пути между всеми порами вершин графа по алгоритму Флойда.

Алгоритм Флойда.

Дан ориентированный граф G=<V,E> с матрицей весов А(Ar­ray [1..N,1..N] Of Integer).

В результате должна быть сформиро­вана матрица D кратчайших расстояний между всеми парами вершин графа и кратчайшие пути.

Идея алгоритма. Обозначим через Dm[i,j] оценку кратчайшего пути из i в j с промежуточными вершинами из множества [1..т]. Тогда имеем:

D°[i,j]:=A[i,j] и

D(m+1)[i,j]= Min{Dm[i,j],Dm[i,m+1 ] +Dm[m+1,j].

Второе равенство требует пояснения. Пусть мы на­ходим кратчайший путь из i в j с промежуточными вершинами из множества [1..(т+1)]. Если этот путь не содержит вершину (m+1), то D(m+1)[i,j]=Dm[i,j]. Если же он содержит эту вершину, то его можно разделить на две части: от i до (m+1) и от (m+1) до j.

Procedure Dist; (*А, D - глобальные структуры данных. *} Var m,i,j:Integer;

Begin

For i: =1 To N Do

For j:=1 To N Do D[i,j] :=A[i,j] ;

For i:=1 To N Do D[i,i]:=0;

For m:=1 Tо N Do

For i : = 1 To N Do

For j:=1 To N Do D[i,j] : =Min {D[i ,j] , D[i,m]+D[m,j] };

End;

Пример. На рисунке 7 представлены графа и значения мат­риц типа D при работе процеду­ры.

Верхний индекс у D (см. рис.8) указывает номер итерации (значение m в процедуре Dist).

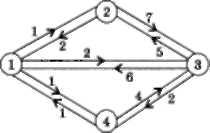
Рис.7

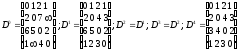Рис. 8

Расстояния между парами вершин дает D. Для вывода са­мих кратчайших путей введем матрицу М того же типа, что и D. Элемент M[i,j] определяет предпоследнюю вершину крат­чайшего пути из i в j.

Процедура Dist претерпит небольшие изменения. В том слу­чае, когда D[i,j] больше D[i,m]+D[m,j], изменяется не только D[i,j], но и M[i,j]. M[i,j] присваивается значение М[m,j]. Для нашего примера изменения М отражены на 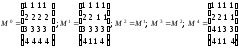рис.9.

Рис.9

Например, необходимо вывести кратчайший путь из 3-й вер­шины во 2-ю. Элемент М[3,2] равен 1, поэтому смотрим на элемент М[3,1]. Он равен четырем. Сравниваем М[3,4] с 3-й. Есть совпадение, мы получили кратчайший путь: 3412.

Procedure All_Way (i, j : Integer) ;{*Вывод пути между вершинами i и j . *}

Begin

If M(i,j]=i Then

If i=j Write(i) Else Write (i, '-' ,j)

Else

Begin All_Way (i ,M[i, j] ) ;All_Way (M[i , j ] , j) ;

End;

End;

Лабораторная работа №4 Построение потока максимальной мощности.

Составить программу построения потока максимальной мощности по алгоритму Форда-Фалкерсона.

Потоки в сетях.

Постановка задачи

Одной из задач теории графов является задача определения максимального потока, протекающего от некоторой вершины s графа (источника) к некоторой вершине t (стоку). При этом каждой дуге (граф ориентированный) (ij) приписана некоторая пропускная способность C(i,j), определяющая максимальное значение потока, который может протекать по данной дуге. Со­держательных интерпретаций задачи достаточно много, и, бе­зусловно, они усилят и сделают более понятными сложные за­нятия по этой проблематике.

Метод решения задачи о максимальном потоке от s к t был предложен Фордом и Фалкерсоном, и их «техника меток» со­ставляет основу других алгоритмов решения многочисленных задач, являющихся обобщениями или расширениями указан­ной задачи.

Одним из фундаментальных фактов теории потоков в сетях является классическая теорема о максимальном потоке и ми­нимальном разрезе. Разрезом называют множество дуг, удале­ние которых из сети приводит к «разрыву» всех путей, веду­щих из s в t. Пропускная способность разреза — это суммарная пропускная способность дуг, его составляющих. Разрез с мини­мальной пропускной способностью называют минимальным разрезом.

Теорема (Форд и Фалкерсон). Величина каждого потока из s в t не превосходит пропускной способности минимального разре­за, разделяющего s и t, причем существует поток, достигающий этого значения.

Теорема устанавливает экви­валентность задач нахождения максимального потока и минима­льного разреза, однако не определяет метода их поиска.

Пример. Показана сеть (рис.10), источник — вершина 1, сток — вер­шина 6, в скобках у дуг указаны их пропускные способности. Минимальный разрез — дуги (1, 2) и (3, 4), следовательно, со­гласно теореме максимальный поток равен 4. Разрез определен путем простого перебора. Логика его «лобового» поиска очевид­на. Осуществляем перебор по дугам путем генерации всех воз­можных подмножеств дуг. Для каждого подмножества дуг проверяем, является ли оно разрезом. Если является, то вычисляем его пропускную способность и сравниваем ее с минимальным значением. При положительном результате сравнения запоми­наем разрез и изменяем значение минимума. Удачный выбор данных позволяет сделать программный код компактным, но очевидно, что даже при наличии различных отсечений в перебо­ре метод применим только для небольших сетей. Однако, как найти максимальный поток, т. е. его распределение по дугам, по-прежнему открытый вопрос.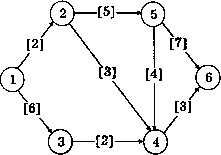

«Техника меток» Форда и Фалкерсона заключается в после­довательном (итерационном) построении максимального пото­ка путем поиска на каждом шаге увеличивающейся цепи, то есть пути (последовательности дуг), поток по которой можно увеличить. При этом узлы (вершины графа) специальным обра­зом помечаются. Отсюда и возник термин «метка».

Пример. Рядом с пропуск­ными способностями дуг указаны потоки, построенные на этих дугах. На рисунке по­ток через сеть равен 10 и найдена увели­чивающаяся цепочка, выделенная «жирны­ми» линиями. Обра­тите внимание на ориентацию дуг, входящих в цепочку. По данной цепочке можно пропустить поток, равный 1, пропуск­ная способность дуги (5, 6). Изменяем суммарный поток, его значение становится равным 11. Поток увеличен, необходимо продолжить поиск увеличивающихся цепочек; если окажется, что построить их нельзя, то результирующий поток максима­лен. Заметим, что для данного примера это значение потока окончательное. Обратите внимание на то, как изменен поток на дугах сети в зависимости от их ориентации.

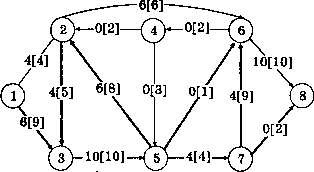
рис.10

рис.11