Приложение 2.

Реализация в MS Excel итерационных методов

Итерационные методы решения уравнений

Описывая метод итераций, обычно о нем говорят как о методе «догадки и проверки». Почти во всех итерационных методах нужно, чтобы пользователь задал начальное приближение. Затем, с помощью этого начального приближения, решается уравнение и вычисляется результат, после чего выполняется проверка, в процессе которой выясняется, достаточно ли близко найденное решение к истинному. Если точность решения, полученного на очередном шаге, неудовлетворительна, процесс повторяется, т.е. выполняется новая итерация. Для эффективного получения итерационных решений важно составить алгоритм, по которому обрабатывается начальное приближение. Рассмотрим следующие итерационные методы решения нелинейных уравнений:

1.Поиск корней с использованием графика.

2.Метод догадки и проверки.

3.Метод прямой подстановки.

4.Метод итерации в ячейке.

5.Решение уравнений с помощью надстройки Поиск решения.

Стандартные формы уравнений

Перед решением уравнения итерационными методами его нужно привести

кстандартной форме. Рассмотрим, к примеру, стандартные формы уравнения

x3 + 4 = 12 x (табл. П2.1).

В методе прямой подстановки и методе итерации в ячейке используется форма 2. Форма 1 обычно более удобна для поиска решения графическим методом; при использовании надстройки Поиск решения применяется разновидность этой формы (в правой части уравнения может находиться любая константа, а не только ноль). Если поиск решения методом «догадки и проверки» осуществляется вручную, то подойдет любая из этих двух форм.

Поиск корней графическим методом

Если есть указания на то, что корень или корни уравнения находятся в ка- ком-либо конечном интервале значений, то в этом интервале можно задать по-

68

следовательность значений. Поочередно подставляя члены этой последовательности в уравнение, проверяем, насколько хорошо оно удовлетворяется при каждом из них, причем, для наглядности, данные удобно представить в графическом виде. При использовании графического метода для поиска корней удобна первая форма уравнения, в которой все его члены перенесены в одну часть. Приведенное выше уравнение в форме 1 можно записать так:

этому уравнению, обычно в результате подстановки различных значений в левую часть уравнения точный ноль получен не будет (если только случайно не попадем на корень). Поэтому перепишем уравнение П2.1 в таком виде:

В ходе поиска решения подставляем различные значения переменной x , и вычисляем значения функции f (x) и строим график зависимости функции

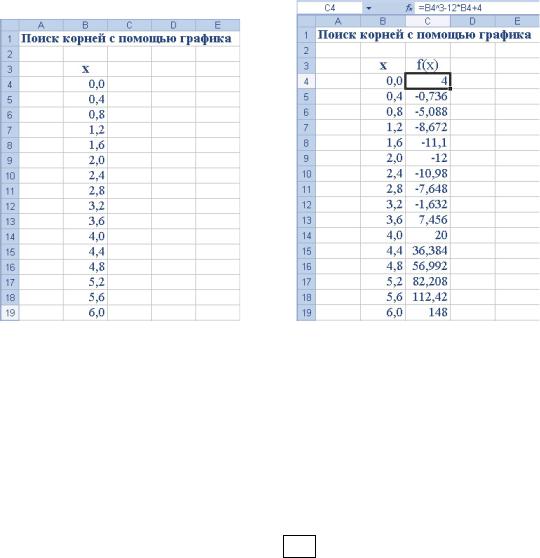
f (x) от x . Корнями уравнения будут значения переменной x , при которых f (x)= 0 . Сначала введем в электронную таблицу столбец значений x в интервале 0 ≤ x ≤ 6 (рис. П2.1).

Затем для каждого x вычислим значение f (x) (рис. П2.2).

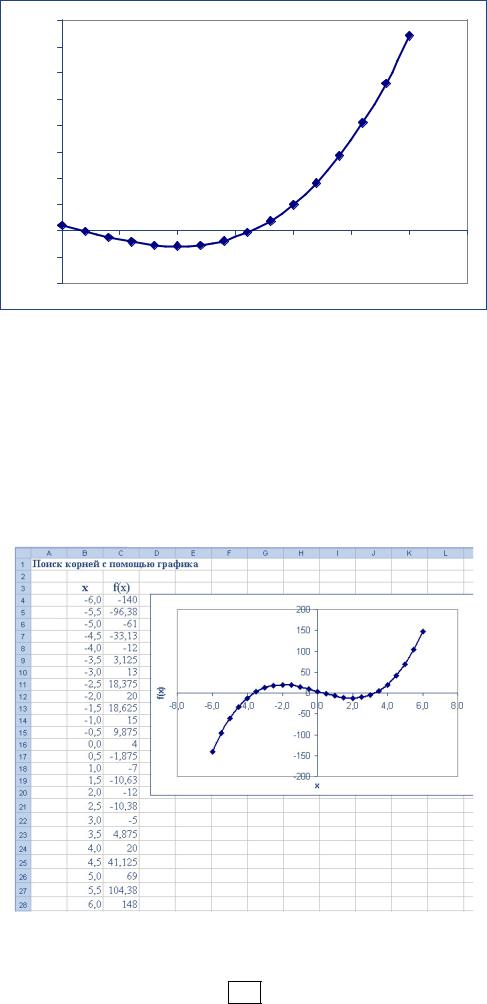
После этого строим точечную диаграмму с графиком функции f (x)

(рис. П2.3).

69

Рис. П2.4 График функции f (x)= x3 − 12 x + 4

70

Издиаграммы П2.4 видно, чтотретийкореньнаходитсявозлеточки x = −3,8 . Графический метод нахождения корней достаточно прост, но обладает низкой точностью. Для нахождения корней с более высокой точностью могут оказаться полезными численные итерационные методы. Применяя эти методы, следует указывать начальные приближения, средством получения которых яв-

ляется графический метод.

Простой итерационный метод догадки и проверки

Если известно, что возле точки x = 0,3 находится корень, одним из простейших способов поиска этого корня является создание электронной таблицы, в которую вводились бы приближенные значения и формула для вычисления функции f (x) (рис. П2.5).

f (x)

Затем следует подобрать такое значение x , для которого f (x) находится

как можно ближе к нулю (в том случае, если уравнение записано в форме 1) (рис. П2.6).

f (x)

Рис. П2.7 показывает, что к корню удалось подобраться довольно близко, однако его точное значение все еще не найдено, поэтому значение функции

f (x) несколько отличается от нуля. Если потребовать, чтобы значение функции f (x) точно равнялось нулю, итерационные методы могут продолжать

свою работу до бесконечности. Вместо этого поиск корней осуществляется с точностью, которая удовлетворяет те или иные потребности. Для оценки точности используется значение допуска (заданная точность), которое рассматривается далее, а пока отметим, что найденное приближение удовлетворяет уравнению с точностью до двух десятичных цифр.

Иногда легче следить за итерационным процессом, если в таблице отображены значения предыдущих оценок и соответствующие им значения функции

(рис. П2.7).

71