Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донбасская национальная академия строительства и архитектуры

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

КЛ по ВТиП-часть2.pdf

Скачиваний:

193

Добавлен:

21.02.2016

Размер:

3.35 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 2111 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Тема 4. Обработка экспериментальных данных

Лекция 7. Интерполирование1

Простейшая задача интерполирования состоит в следующем. Пусть на некотором отрезке [a,b] заданы n + 1 точки x0 , x1 ,..., xn , которые называются уз-

лами интерполяции, и значения функции f (x) в этих точках

Требуется построить функцию F (x) (интерполирующая функция), принадлежащею определенному классу и принимающую в узлах интерполяции те же значения, что и f (x), т.е. F (x0 )= y0 , F (x1 )= y1 , F (xn )= yn .

Геометрически это означает, что нужно найти кривую y = F (x) опреде-

ленного типа, проходящую через заданные точки.

В такой постановке задача либо имеет бесчисленное множество решений либо не одного.

Если же функцию F искать в виде полинома Fn (x) степени n, то задача становится однозначной. Полученную интерполяционную формулу y = F (x) обычно используют для приближенного вычисления значений данной функции f (x) при значениях аргумента x , отличных от узлов интерполирования. Такая операция называется интерполированием функции f (x). Более точно, различают интерполирование в узком смысле, когда x x0 , xn и экстраполирование, когда x x0 , xn . Мы будем и первую и вторую операцию понимать как интерполирование.

Постановка задачи

Некоторая функция		y = f (x)	задана таблицей своих значений на множе-
стве равностоящих значений аргумента x .
	x	x1		x2	…	xn
	y	y1		y2	…	yn

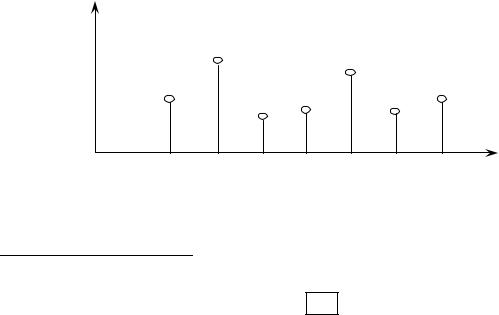
На графике это выглядит следующим образом (рис. 7.1):

		y2
	y1		yn
	x1	x2	xn
Рис. 7.1	Значения функции		y = f (x) на множестве равностоящих

значений аргумента x

1 Данная тема предназначена для самостоятельного изучения

Чтобы найти значение функции при любом значении аргумента x , необходимо построить аналитическую функцию F (x), которая совпадала бы с не-

известной функцией f (x) в узлах таблицы и приближалась бы к ней вне узлов. Тем самым, будет, как бы восстановлена неизвестная функция f (x) замененная теперь на известную – F (x). Степень погрешности интерполяции, т.е. разность f (x)− F (x) при заданном значении x зависит от ширины интервала h = xi+1 − xi и от вида интерполирующей функции.

Линейная интерполяция

Значения функции вне узлов таблицы проще всего вычислить, заменяя неизвестную функцию на каждом отрезке [xi , xi+1 ] линейной функцией

F1 (x)= b0 + b1 x ,

(7.1)

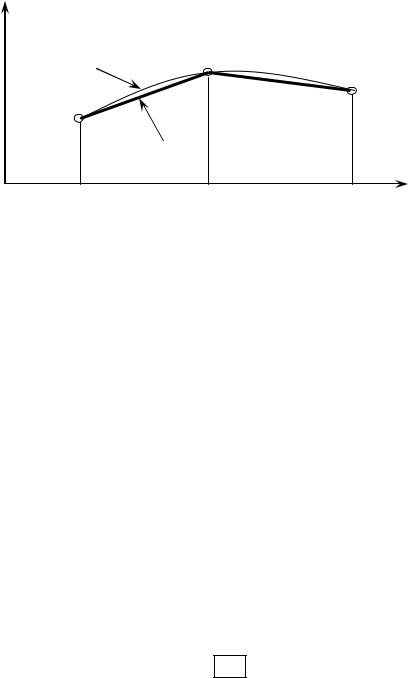
т.е. отрезком прямой, соединяющим узловые точки таблицы (рис. 7.2).

y
	f(x)		y2
	y1
		F(x)
	x1	x2	x
			x
Рис. 7.2	Графическое представление линейной интерполяции

Неизвестные коэффициенты b0 , b1 определяются из решения системы уравнений, полученной из предположения, что значение неизвестной функции f (x) и значение функции F1 (x) совпадают в узлах x1 и x2 .

Квадратичная интерполяция

Линейная интерполяция, как это видно из рис. 7.2, имеет большую погрешность. Чтобы уменьшить погрешность, неизвестную функцию f (x) интерполируют полиномом второй степени.


F2 (x)= b0 + b1 x + b2 x2		(7.2)
Т.е. через три точки (y1 , x1 );	(y2 , x2 ); (y3 , x3 ) проводят параболу (7.2).
Значения коэффициентов b0 , b1 , b2	находят решая систему трех уравнений, по-
лученных из предположения, что значение неизвестной функции		f (x) и зна-

чение полинома F2 (x) совпадают в узлах x1 , x2 , x3 .

Интерполяционный полином любой n-ой степени можно построить, имея n + 1 узел таблично заданной функции. Эти полиномы Fn (x) называются ин-

терполяционными полиномами Лагранжа.

Полиномы Лагранжа дают хорошее качество интерполяции при большом количестве узлов и высокой степени полинома. Однако у полиномов Лагранжа есть два важных недостатка:

9Существуют функции, при интерполяции которых, увеличение степени полинома не дает хорошего приближения.

9Интерполяционные полиномы Лагранжа в узлах соединения имеют изломы. Это крайне нежелательное явление, т.к. возникают трудности с дифференцированием и интегрированием такой функции.

Интерполяционная формула Лагранжа.

Лагранжем введена формула для интерполирования, которая является более общей, т.к. она применима для случая произвольного расположения узлов

интерполяции (неравномерно расположенных)

Пусть

на

отрезке

[a,b]

даны

n + 1 различных

значений

аргумента

x0 ,x1 ,..., xn

и известны соответствующие значения функции

f (x);

f (x0 )= y0 ,

f (x1 )= y1 ,…, f (xn )= yn

Требуется построить полином Fn (x) степени не выше n, имеющий в за-

данных

узлах

x0 ,x1 ,..., xn

те

же значения, что

функция

f (x),

т.е.

Fn (x0 )= y0 , Fn (x1 )= y1 ,…, Fn (xn )= yn .

1) Сначала решим такую задачу:

построить полином Pi (x)

такой,

что

Pi (x j )= 0 при

j ≠ i и Pi (xi

)= 1, т.е. это можно записать так:

Pi (x j )

= δij

(символ Кронекера)

Так

как

исходный

полином

обращается

точках:

x0 ,x1 ,..., xi−1 ,xi+1 ,..., xn , то он имеет вид:

Pi (x)= Ci

(x − x0 ) (x − x1 ) ... (x − xi−1 ) (x − xi+1 ) ... (x − xn )

(7.3)

где Ci

– постоянный коэффициент; не зависящий от x .

Ci найдем из (7.3) положив x = xi

и учитывая, что Pi (xi )= 1, т.е.

Ci (xi − x0 ) (xi − x1 ) ... (xi − xi−1 ) (xi − xi+1 ) ... (xi − xn )= 1

((xi − x0 ) (xi

− x1 ) ... (xi − xi−1 ) (xi − xi+1 ) ... (xi − xn ))

Подставив это в (7.3), получим:

(x)=

(x − x0 ) (x − x1 ) ... (x − xi−1 ) (x − xi+1 ) ... (x − xn )

((xi − x0 ) (xi − x1 ) ... (xi − xi−1 ) (xi − xi+1 ) ... (xi − xn ))

Т.е. задача первая решена.

2) Теперь решим более общую задачу отыскания Fn (x)

Этот полином имеет вид:

Fn (x)= ∑Pi (x) yi

i=0

Всамом деле, степень его не выше n и он принимает значения yi в точках

x= xi . Т.е. искомый полином имеет вид:

n			(x − x0 ) (x − x1 ) ... (x − xi−1 ) (x − xi+1 ) ... (x − xn )
Fn (x)= ∑yi						(7.4)
Fn (x)= ∑yi		((xi − x0 ) (xi − x1 ) ... (xi		− xi−1 ) (xi	− xi+1 ) ... (xi − xn ))	(7.4)
i=0		((xi − x0 ) (xi − x1 ) ... (xi		− xi−1 ) (xi	− xi+1 ) ... (xi − xn ))
Это – интерполяционная формула Лагранжа
Вычисление Лагранжевых коэффициентов
Если формулу (7.4) записать в виде:
	n
Fn (x)= ∑Fi(n) (x) yi , то
F (n) (x)=i=			0 (x − x0 ) (x − x1 ) ... (x − xi−1 ) (x − xi+1 ) ... (x − xn )			(7.5)
F (n) (x)=i=						(7.5)
i			((xi − x0 ) (xi − x1 ) ... (xi	− xi−1 ) (xi	− xi+1 ) ... (xi − xn ))
			((xi − x0 ) (xi − x1 ) ... (xi	− xi−1 ) (xi	− xi+1 ) ... (xi − xn ))

называют Лагранжевыми коэффициентами.

В случае постоянного шага h существуют таблицы для Лагранжевых коэффициентов и вычислять их не надо.

Интерполяция сплайном

Для проведения гладкой кривой через узловые точки (y1 , x1 ); (y2 , x2 ); … (yn , xn ) обычно используют гибкую стальную линейку. Ее ставят на ребро и

закрепляют в узлах. Ось линейки описывает при этом гладкую кривую, которая и будет интерполировать заданную таблицей функцию. Полученная таким образом интерполяционная функция называется сплайном. Сплайн функция не имеет недостатков полиномов Лагранжа. У нее нет изломов, и гибкая кривая легко принимает на одном участке вид прямой, а на соседнем вид параболы.

Численные значения коэффициентов сплайн полиномов определяют из следующих условий:

9Значение полинома равно значению искомой функции в узлах таб-

лицы.

91-я и 2-я производные сплайн полиномов слева и справа от любого узла таблицы равны друг другу. Это означает, что сплайн функция не имеет в узлах таблицы не только изломов, но и смены радиусов кривизны.