304 6. Как происходит разрушение при кручении материалов в пластичном и
хрупком состоянии?
Раздел 5 Плоский прямой изгиб
Вэтом разделе рассматривается 8 тем: внутренние силовые факторы и правило знаков, дифференциальные зависимости между Q, q и М, построение эпюр, определение напряжений в поперечных сечениях, геометрические характеристики поперечных сечений, расчет на прочность, аналитический способ определения перемещений и графоаналитический метод определения перемещений. После изучения этого раздела студент должен решить задачу №5 контрольной работы №1 (для изучающих курс СМ в объеме 180 часов) и задачу №6 контрольной работы №2. Для изучающих курс в объеме 100 часов задача №5 входит в контрольную работу № 2.
Вконце раздела даны вопросы для самопроверки. Знания, полученные после
изучения этого раздела должны быть проверены по тесту №5.
5.1.Внутренние силовые факторы. Правило знаков
Вобщем случае в плоскости поперечного сечения возникают 2 внутренних силовых фактора – поперечная сила Q, которая определяется как алгебраическая сумма проекций всех сил, действующих по одну сторону от сечения на одну ось, и изгибающий момент М, как алгебраическая сумма всех моментов по одну сторону от сечения относительно центра тяжести этого сечения.
Поперечная сила Q принимается со знаком «+», если при подходе к сечению слева внешняя сила направлена вверх, изгибающий момент М принимают со знаком «+», если внешний момент действует по часовой стрелке
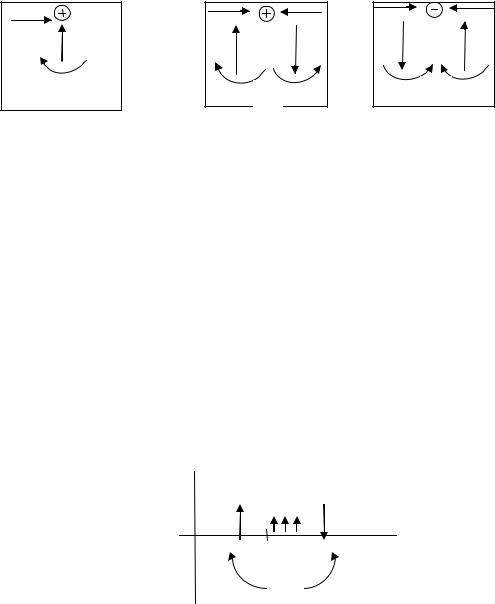
305
при подходе к сечению слева. Одно общее правило (рис. 5.1, а), все остальное наоборот (рис. 5.1 б, в).
|
Q |
Q |
|
|
|
М |
M |
M |
M |
а) |
б) |
в) |
Рис. 5.1
5.2. Дифференциальные зависимости между Q, q и М.
Выведенные Д. И. Журавским дифференциальные зависимости дают возможность проверить правильность построения эпюр.
Q |
q |
Q+dQ |
|
|
|
|
dx |
|
|
|
|
|
|
M M+dM
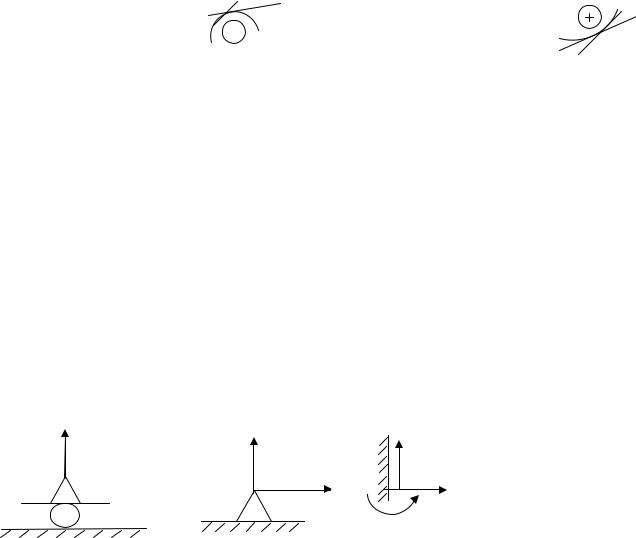
Рис. 5.2
Рассмотрим равновесие элемента длиною dx (рис. 5.2) :
Q + qdx − Q − dQ = 0
q = dQdx
(5.1)
306
tgβ- тангенс угла наклона касательной к эпюре Q
q < 0 |
|
|
|
2 |
|
|
q > 0 |
|
|
||
M + Qdx + q |
dx |
− M − dM = 0, |
Q = |
dM |
|
, |
( |
||||
2 |
|
dx |
|||||||||
5.2) |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
d 2 M |
|
|
|
|
|
|
|
|
|
|
|
q = |
|
|
|
|
(5.3) |
|
|
|
|
|
|
dx2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
5.3. Построение эпюр Q и М
Алгоритм решения задачи :
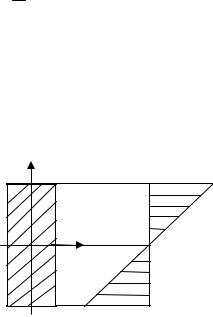
1.Показать все силы, действующие на балку. Рассмотреть возможные типы опор:
RA |
RA |
RA |
HA MR HA
2.Составить возможные уравнения статистики.
3.Решить уравнения статики и определить реакции опор.
4.Разбить балку на участки.
Примечание: для консольных балок, если идти со стороны свободного конца, решения можно начинать с п. 4.
5.На каждом из участков составить аналитические выражения для поперечной силы и изгибающего момента.
6.Подставить числовые значения и найти характерные точки, дающие возможность построить эпюры Q и M.
7.Найти положение опасного сечения.
307
8. Используя условие прочности (5.8). Определить величину момента инерции сечения (Woc ).
9. По полученному значениюWoc определить размеры сечения.
5.4. Определение напряжений
Отдельное волокно при изгибе балки испытывает простое растяжение – сжатие. σ = Еε(закон Гука) ;ε = ρу, тогда
σ = Е |
у |
. |
(5.4) |
|
|||
|
ρ |
|
|
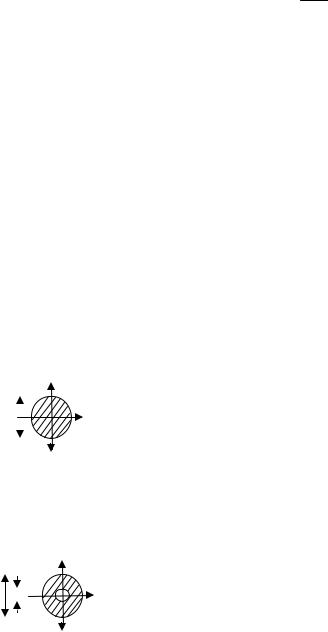
Эпюра нормальных напряжений по высоте сечения имеет вид (рис. 5.2).
y |
z |
"σ " |
Рис. 5.3 |
Зависимость (5.4) можно представить в виде |
|
|
||||||||
|
|
1 = |
σ |
|
|
|
|
|
|
|
|
|
Еу |
|
|
|
|
|
|
||
(5.5) |
|
ρ |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
M z и |
|
Рассмотрим |
зависимость |
между |
|
|
действующим |
моментом |
||||
возникающими |
в поперечном |
сечении |
σ: |
M z = ∫σydA |
учитывая, |
что |
||||
J z = ∫ y2dF получаем: M z = E J z ; или |
|
|
|
|
|
A |
|
|
||
|
|
|
|
|
|
|
|
|||
A |
ρ |
|
1 |
|
|
M z |
|
|
|
|
|
|
|
= |
|
|
|
|
|||
(5.6) |
|
|
ρ |
ЕJ z |
|
|
||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Сравнивая формулы (5.5) и (5.6) получаем формулу Навье
|
308 |
|
|
||
|
|
σ = |
M z |
y |
|
|
|
||||
(5.7) |
|
|
J z |
||
J z |
|
|
|
||
учитывая, что |
=Wz , получаем условие прочности при изгибе |
||||
|
|||||
|
ymax |
|
|
||
σmax = M z ≤[σ]
Wz
( 5.8)
5.5. Геометрические характеристики поперечных сечений
Геометрическими характеристиками сечений, определяющими способность стержня сопротивляться деформации, являются: площадь, положение центра тяжести, статические моменты, моменты инерции, моменты сопротивления.
В таблицу сведены формулы для некоторых поперечных сечений:
|
|
Сечение |
|
|
Jz |
|
|
|
|
J y |
|
|
|
Wz |
|
|
|
Wy |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Круг |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
y |
|
|
πd 4 |
|
|
|
πd 4 |
|
|
|
πd 3 |
|
|
πd 3 |
|
|
|||
“ |
|
|
|
|
z |
|
|
64 |
|
|
|
|
64 |
|
|
|
32 |
|
|
32 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полый вал |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
α = |
d |
|
|
|
|
|
πD4 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
D |
|
πD4 |
(1−α |
4 |
) |
(1−α |
4 |
) |
πD3 |
(1−α |
4 |
) |
πD3 |
(1−α |
4 |
) |
||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
y |
|
64 |
|
64 |
|
|
32 |
|
32 |
|
||||||||
D d |
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сечение |
|
|
Jz |
|
|
|
|
J y |
|
|
|
Wz |
|
|
|
Wy |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
309 |
|
|
|
|
|
|
|
|
|
Прямоугольник |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
bh3 |
|
|
hb3 |
|
|
bh2 |
|
hb2 |
|||
|
|
|
|
|
|
|
|
|
|||||||
h |
|
z |
|
12 |
|
|
12 |
|
|
6 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Прямоугольник с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отверстием |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BH |
3 |
bh3 |
HB |
3 |
hb3 |
BH 2 |
bh2 |
HB2 |
hb2 |
||
|
|
y |
в |
12 |
− |
12 |
12 |
− |
12 |
6 |
− |
6 |
6 |
− |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
h |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
5.6. Расчет на прочность
В общем случае в плоскости сечения возникают поперечная сила (Q), которая вызывает касательные напряжения, вычисляемые по формуле Журавского
|
|
|
|
|
QS |
отс |
||
|
|
|
τ = |
|
|
н.о. |
, |
|
|
|
|
|
|
||||
|
|
|
|
|
|
Jb |
||
(5.9) |
|
|
|
|
|
|
|
|
где Q – поперечная сила в сечении, где определяются напряжения, |
||||||||
Sнотс.о. - статический момент отсеченной части относительно нейтральной оси |
||||||||
(см. п. 5.2) |
S отс |
= А |
|
z |
н.о. |
|||
|
н.о. |
|
отс |
|
||||
J- момент инерции всего сечения, |
|
|
|
|
|
|
|
|
b – ширина сечения |
в том месте, где определяется напряжение и изгибающий |
|||||||
момент М, который вызывает нормальные напряжения (формула 5.4 п. 5.3) |
||||||||
|
σ = |
|
M z |
|
y . |
|
|
|
|
|
J z |
|
|
||||
|
|
|
|
|
|
|
||
310
В этом случае полную проверку прочности следует провести по одной из гипотез прочности (рис. 3.2).
5.7. Аналитический способ определения перемещений
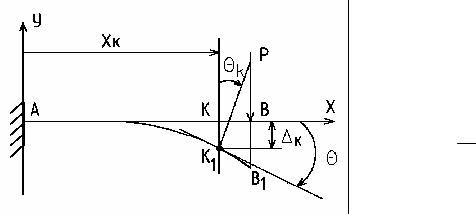
При изгибе ось балки искривляется. В силу малости деформаций и при условии, что вертикальная ось является главной можно считать, что при изгибе центры тяжести поперечных сечений перемещаются по вертикали. Такое перемещение называются прогибом сечения. Прогиб к сечения xk
(рис.5.4)считается положительным, если центр тяжести сечения перемещается вверх. Кроме этого, каждое сечение, оставаясь плоским, поворачивается вокруг нейтральной линии на некоторый угол, который называется углом поворота сечения. Угол поворота Θк сечения (рис. 5.4) считается положительным, если сечение поворачивается против хода часовой стрелки.
K = y(x) при x = xK
ΘK = dydx при x = xK
Рис. 5.4
Изогнутую ось балки называют упругой линией. Уравнение упругой линии, представляющее функциональную связь между прогибом у и координатой х сечения y=y(x), зависит от внешней нагрузки, материала балки, размера и формы поперечного сечения. Если вид функции y(x) известен, то прогиб
произвольного поперечного |
сечения |
с координатой хк можно найти как |
|
значение функции y(x) при |
х=хк , а угол поворота этого сечения будет равен |
||
значению первой производной |
dy(x) |
при х=хк. Вид функции у(х) можно |
|
|
|
dx |
|
найти из приближенного дифференциального уравнения упругой линии.
311
Если направить ось у вверх, то для балки постоянного поперечного сечения приближенное дифференциальное уравнение упругой линии имеет вид
EJ z y′′(x) = M z (x) ,
где Е – модуль упругости материала, J z - осевой момент инерции поперечного сечения, M z - изгибающий момент в произвольном поперечном сечении на последнем грузовом участке балки.
Проинтегрировав это дифференциальное уравнение два раза, |
получим два |
|
уравнения: |
|
|
x |
|
|
EJ z y′(x) = ∫M z (x)dx + C |
(*) |
|
0 |
|
|
x |
x |
|
EJ z y(x) = ∫dx∫M z (x)dx + Cx + D |
(**) |
|
0 |
0 |
|
Уравнение (*) служит для определения угла поворота сечения, а уравнение (*) –
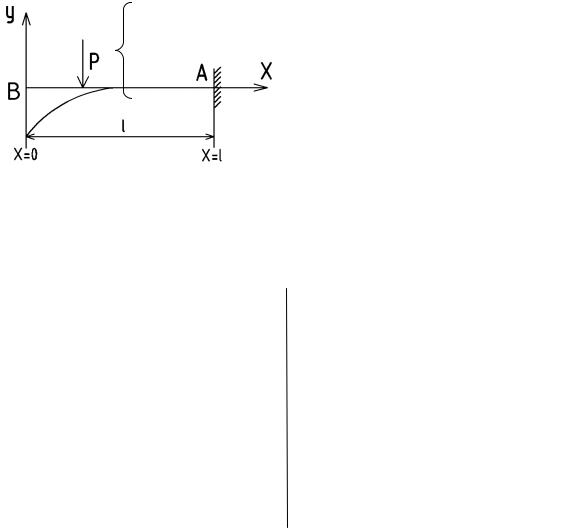
для определения прогиба сечения. В эти уравнения входят постоянные интегрирования С и D. Они определяются из граничных условий, зависящих от условий закрепления балки:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Граничные |
|
|
условия. |
|
|
|
|
||
1) |
|
= у(х) |
|
|
|
= 0 → (* * ) |
|
1)θ = у/ (х) |
|
|
= 0 → (* ) |
||||
|
|
|
|
|
|
|
|||||||||
|
А |
|
|
Х=ХА |
|
|
|
|
А |
|
Х=l |
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||
2) В = у(х) |
|
Х=ХВ |
= 0 → (* * ) |
|
2) A = у(х) |
|
|
Х=l |
= 0 → (* * ) |
||||||
|
|
|
|||||||||||||
312
Метод определения перемещений, основанный на интегрировании дифференциального уравнения упругой линии, называют аналитическим методом определения перемещений.
Примеры на составление и интегрирование приближенного дифференциального уравнения упругой линии приведены в [ 2 ].
5.8. Графоаналитический метод определения перемещений
Универсальным способом для определения линейных и угловых перемещений в любых системах, состоящих из шарнирно соединенных брусьев
является метод Мора.
При отыскании линейного перемещения (прогиба) к системе,
освобожденной от заданных нагрузок, в направлении искомого перемещения в заданной точке прикладывается безразмерная единичная сила. Аналогично, при
определении углового перемещения в заданном сечении прикладывается пара сил с моментом, равным безразмерной единице.
Формула (интеграл) Мора для определения перемещений имеет вид:
|
КР = ∑ ∫ |
M P M1 |
dx , |
||
|
|
||||
|
li |
EJ |
z |
||
|
|
||||
где |
KP - искомое перемещение |
(линейное или угловое). Первый индекс |
|||
указывает точку, в которой определяется перемещение. Индекс Р означает, что
определяется перемещение от заданных нагрузок;
M P и M1 - аналитические выражения изгибающих моментов от заданной нагрузки и единичной силы (момента) соответственно.
Суммирование производится по грузовым участкам, li -длина i-го грузового участка.
В случае балки постоянного поперечного сечения с прямолинейной осью интеграл Мора удобно вычислять графоаналитическим методом, применяя правило Верещагина. По этому правилу интеграл Мора для отдельного i-го
313
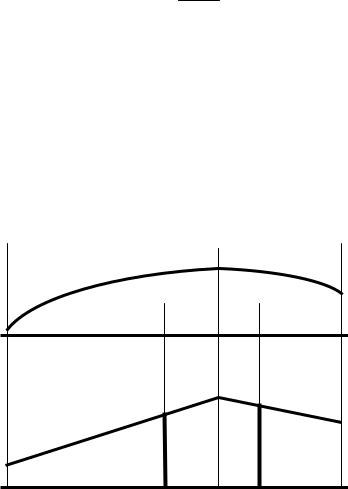
участка балки вычисляется как произведение площади нелинейной эпюры изгибающих моментов на ординату линейной эпюры изгибающих моментов, взятую под центром тяжести нелинейной, деленную на жесткость поперечного сечения. Таким образом, при применении правила Верещагина вычисление перемещения ведется по формуле
KP = ∑ωiηci ,
EJ z
где ωi - площадь нелинейной эпюры изгибающих моментов;
ηci - ордината линейной эпюры изгибающих моментов, соответствующая центру тяжести нелинейной;
EJ z - жесткость поперечного сечения балки.
Смысл параметров ωi и ηci пояснен на рис. 5.5.
|
|
ω1 . |
.M P ω2 |
|
|
|
|
M1 |
|
|
|
ηc1 |
ηc2 |
|
|
|
Рис. 5.5 |
|
|
Произведение |
ωiηci |
считается |
положительным, если часть эпюры, |
|
имеющая площадь ωi , и соответствующая ордината ηci |
расположены по одну |
|||
сторону от базы эпюры. |
|
|
|
|
Применение правила Верещагина подробно рассмотрено в [ 2 ]. |
||||