
- •Глава 3
- •3. Деякі реальні проблеми та їх вирішення
- •3.1 Прогнозування вартості: створення, переробка або зміна вимірювальної сітки
- •3.1.1 Детерміновані точка зору: Інтерполяція і наближені методи
- •3.1.1.1 Узагальнені середнє арифметичне, 1d
- •3.1.1.5 Кубічні сплайни (1d-типу)
- •3.1.1.6 Поліноміальна регресія (1d-випадку)
- •3.1.1.7 Поліноміальна регресія (2d-чохол)
- •3.1.1.8 В-сплайни (1d-випадку)
- •3.1.1.9 B-сплайни (2d-вигляд)
- •3.1.2 Стохастична точка зору: Методи геостатистики
- •3.1.2.2. Звичайний Крігінг
- •3.1.2.3 Універсальний крігінг
- •3.1.2.4 Крос-перевірка
3.1.1.7 Поліноміальна регресія (2d-чохол)
Почнемо з нашого знайомого, наприклад, і пояснити це в деталях. Тоді ми можемо уявити загальне правило.
Приклад 3.1.1.2 '' (2D-чохол) Знову ж таки, ми вважаємо, наступні вимірювання:
z1 = z (x1,y1) = z (1, 0) = 0,1, z2 = z(x2,y2) = z (4, 0) = 0,2,
z3 = z (x3,y3) = z (1, 1) = -0,1, z4 = z(x4,y4) = z (4, 1) = -0,2.
Ми припускаємо, що структура даних випливає z(x,y) = a10 • х + a01 • у +a00. Двовимірний многочлен в цій формі має бути визначено. Очевидно, що це є многочлен двовимірний першого ступеня. Основна ідея цього наближення слід підхід до 1D-випадку. Ми шукаємо параметрів a10, a01, a00, які призводять до
![]() (*.1)
(*.1)
Використання приватні похідні за цими параметрами, ми отримуємо:
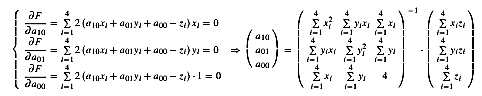
При заданих значень з нашого набору даних, ми отримаємо:
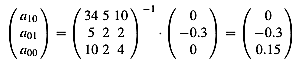 (*
0,2)
(*
0,2)
і
функціональна залежність визначається
як площина або двовимірної полінома
першого ступеня виду z(x,y)
=
0 x-0.3
x-0.3 y+0.15(див.рис.
3.5).
y+0.15(див.рис.
3.5).
Загальне правило для двовимірної полиномиальної регресії виглядає наступним чином:
Нехай наступні дані бути надана: z1 = z (x1,y1), ..., zN = z (xN,yN). Функціональне співвідношення виду до
![]()
шукається таким чином, що наступне необхідна умова виконується:
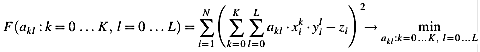

Рис.3.5
Ця умова приводить до
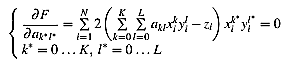
і після деякого спрощення (K + 1) (L + 1) рівнянь в наступному
LSE:
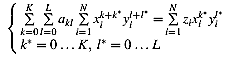 (3-11)
(3-11)
Вирішення цієї LSE параметрів призводить до akl, k = 0 ... K, l = 0 ... L.
Точність полиномиальной апроксимації дані можуть бути Де-
описувана
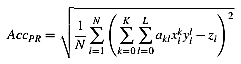 (3-11′)
(3-11′)
з параметрами, які вирішити (3-11). Для перевірки моделі це значення має бути в порівнянні з Zmax - Zmin.
2
Примітка: У разі N = (M + 1) (L + 1), поліном виходить, що виконує вимогу інтерполяції. Матриця LSE (3-11) може бути нерегулярним. Таким чином, деякі необхідні умови повинні бути доведено, перш ніж намагатися вирішити LSE. Навіть у випадку регулярної матриці може бути чисельне проблеми, наприклад, для великих N.
Після 1D-випадку, припущення про полиномиальной структурі даних повинна бути відхилена, якщо точність порівнянна з zmax - zmin. Більш складні функціональні структури представлені в п. 3.2.1 і гол. 4.
3.1.1.8 В-сплайни (1d-випадку)
Позначення "B-сплайни" сходить до французьким математиком Безьє. Основна ідея підходу виходить з алгоритму, заснованого на алгоритмі Катестеляу повторної лінійної інтерполяції. Цей метод успішно використовується в сучасних CAD-інструментів. B-сплайни добре підходить для додатків, які повинні бути виконані без урахування координат. B-сплайни і B-поверхні параметрически визначений.
Так звані B-криві визначають за допомогою одного параметра, т. Більш загальні B-поверхні відповідають інтерполяції з двома параметрами, і та ін. Зміна системи координат (масштабування осей та інших афінних перетворень) НЕ вплив основний алгоритм або зміна вимірювальної сітки в тривимірному просторі E3.
Для плоских кривих в Е2 координату у слід опустити в наступних рівняннях.
Сформулюємо загальне правило для побудови B-кривих наступним чином:
Нехай
 ,буде N+1 точок даних і
,буде N+1 точок даних і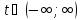 буде параметром. Після лінійної
інтерполяції для N-разів з фіксованим
параметром t для
буде параметром. Після лінійної
інтерполяції для N-разів з фіксованим
параметром t для
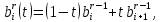
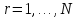
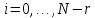
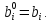
B
результаті отримана точка
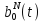 є точкою на B-кривій
є точкою на B-кривій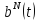 ступеня
N.
ступеня
N.
Примітка: Пам'ятайте, що нумерація точок починається з нуля. Отже, ми маємо N+1 точок даних. Співвідношення (3-12) відноситься до всіх координат даних, а саме, х, у, z (див. Приклад 3.1.1.4).
B-крива
 є параметричною і відповідає точці
є параметричною і відповідає точці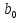 дляt
= 0 і точці
дляt
= 0 і точці
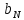 дляt
= 1. Ця крива звивається поміж іншими
точками (рис. 3.6), що пояснює той факт, що
інтерполяцію з B-сплайнами називають
інтерполяцією кінцевої точки. Полігон,
побудований на основі точок
дляt
= 1. Ця крива звивається поміж іншими
точками (рис. 3.6), що пояснює той факт, що
інтерполяцію з B-сплайнами називають
інтерполяцією кінцевої точки. Полігон,
побудований на основі точок
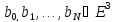 називається
полігоном Безьє або контрольним полігоном
В-кривої
називається
полігоном Безьє або контрольним полігоном
В-кривої
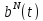 .
.
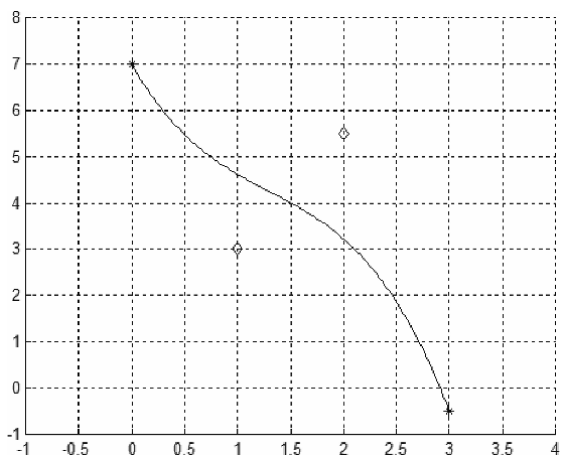
Рис. 3.6 B-крива за даними прикладу 3.1.1.4
Приклад 3.1.1.4 (1D- Вигляд) дані такі часові виміри:
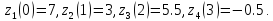
За умовою (3-12) це відповідає
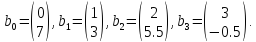
Отже, як параметрична крива, що описує цю структуру з фіксованими кінцевими точками, виглядає насправді? Тут N = 3. Таким чином, потрібно виконати три кроки інтерполяції для отримання остаточної B-кривої з (3-12). Перший крок призводить до
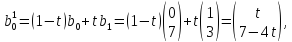
 (*.1)
(*.1)
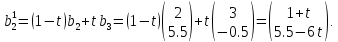
Це
три додаткових точки, що належать до
ліній
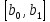 ,
, ,
,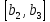 і поділяють їх на однакові частини,
залежно від t. На другому кроці ми
отримуємо
і поділяють їх на однакові частини,
залежно від t. На другому кроці ми
отримуємо
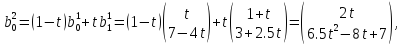
 (*.2)
(*.2)
Ці
дві точки лежать на лініях
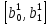 ,
,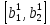 і поділяють їх на рівні частини в
залежності від t. На останньому кроці,
параметрична В-крива визначається
і поділяють їх на рівні частини в
залежності від t. На останньому кроці,
параметрична В-крива визначається
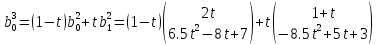 (*.3)
(*.3)
І зображується, як показано на рис. 3.6.
Просте виконання і незалежність систем координат є перевагами цього підходу. Грубий підхід можна покращити згладженням, звивистістю лінії, використовуючи B-сплайни. Крім того, деякі підходи - полігони з однаковими кінцевими точками і такою ж кількістю точок - слід порівняти на основі їх аналітичної параметричної форми заданої (3-12). Наприклад, таким чином можна побудувати полігон (посередній). Одним незначним недоліком може бути нетрадиційне параметричне представлення B-сплайнів.
