
- •3.2.1.2 Наближення з перетворенням Фур'є (1d)
- •3.2.1.3 Наближення 1d-сплески
- •3.2.2 Стохастична точка зору: Випадкові процеси та корисні кількісні характеристики
- •3.2.2.1 Змінна середньої
- •3.2.2.2 Геометричне згладжування часових рядів.
- •3.2.2.3.Розгляд сезонної складової.
- •3.2.2.4 Час серії моделювання з використанням випадкових процесів
- •3.2 Опис представленої "Змішаної" у вимірах за допомогою аналітичної функції.
- •3.2.2.5 Прогнозування з накладенох моделі
- •3.2.2.6 Продовження прикладу 3.2.2.4
- •3.3 Врахування вплив простору, часу та інших факторів
- •3.3.1 Класичний Коефіцієнт кореляції, кореляційна функція, і вплив функції
- •3.3 Врахування впливу простору, часу та інших факторів що відповідає в нашому випадку
- •3.3.2 Точки і знаки: Парна і точкова кореляційна функція і точковий процес статистики.
- •3.3.2.1 Однорідні Пуассонові поля.
- •3.3.2.3 Matern Cluster Fields

3.14 Лінійна регресія підхід (* .11) підгонки даних з прикладу 3.2.1.1

Визначення 3.2.1-1 Нехай U, V два регулярних функцій, визначених для інтервалу [а, Ь].
Далі, нехай W буде невід'ємна функція визначена для того ж інтервалу. наступнезначення називається скалярний добуток функцій U, V по відношенню до маси.
Функція W:

Приклад 3.2.1.2 Розрахунок скалярного твору для таких функцій:

Визначення 3.2.1-2 Дві регулярні функції U, V визначені для інтервалу [а, Ь]
називаються
ортогональними, якщо їх скалярний
добуток дорівнює нулю. Важливість
ортогональних функцій у функціональних
просторах аналогічно
ортогональних
базисних векторів в евклідовому просторі.
Аналогічно поданням
будь-який
вектор у вигляді суми базисних векторів,
будь-яка функція F (х), визначена на
відрізку [а, b]
може
бути апроксимована за допомогою
ортогональних функцій![]()

Приклад 3.2.1.3 Чи многочлени 1, х, х2,. , , ортогональні по відношенню доІнтервал [a.б]? Ми можемо відповісти на це питання, використовуючи Визначення 3.2.1-1 і 3.2.1-2:

Таким чином, ці многочлени НЕ ортогональні, але лінійно незалежні, що означає, що це не можливо уявити такого полінома у вигляді зваженої суми або лінійний.
Поєднання з іншими полиномов:

Існує метод генерації системи ортогональних функцій з linearindependent система функцій, які називаються грам-Шмідта:
![]() бути
лінійно-незалежні функції на
бути
лінійно-незалежні функції на
Інтервал
[a.б].
Функції
![]() заснований
на
заснований
на![]() побудувати
ортогональний базис на відрізку
побудувати
ортогональний базис на відрізку
[а,Б]:

Константи, що використовуються тут, можуть бути обчислені за допомогою:
![]()
Розглянемо приклад 3.2.1.3? довести методом Грама-Шмідта.
Приклад
3.2.1.3? Наступна системи![]() повинен
бути ортогоналізуются
повинен
бути ортогоналізуются
на [-1, 1]. Використовуючи (3-55), ми отримаємо послідовно:

Малюнок 3.15 показує перші три функції цього ортогонального базису на інтервалі
[-1, 1].

Інжир. 3.15 Перші три функції, E1 (х) (суцільна), е2 (х) (пунктирна) і E3 (х) (пунктирна), ортогональної основою із прикладу 3.2.1.3?
Приклад 3.2.1.4 Доведемо, що системи
![]()
ортогональна на [-π, π]. Ми можемо спочатку довести наступне:

Для (* .1) і (* 0,2) такі відомі тригонометричні співвідношення можуть бути використані:

Для інтеграла в (*) .3,

тримає. Цей факт враховується в прикладі 3.2.1.4 використовується для побудови функціональної наближення перетворення Фур'є, наближення, що має сенс
Для даних, що характеризуються хвильової структури. Ми розглядаємо цю тему коротко;
Докладніше можна знайти в Bracewell (1978) і Хеммінга (1973).
3.2.1.2 Наближення з перетворенням Фур'є (1d)
Ми
обмежимося тут в одновимірному випадку.
вимірювання![]() від
невідомої функціїz
(х) повинна бути наближена
від
невідомої функціїz
(х) повинна бути наближена
в [-π, π] за наступною аналітичної функції:

Використання (3-53) і (3-54), ми можемо представити цю функцію у вигляді


Тут ми використовуємо співвідношення (* .1) - (. * 3) з прикладу 3.2.1.4. Як було показано вище, ми отримуємо рівняння для розрахунку коефіцієнтів, де коефіцієнт задається як невід'ємної і залежить від безперервного, але невідомої функції z (х).
Таким чином, ці рівняння також повинні бути "переведені" в дискретної формі, заснованої на даних вимірювань
![]()
Це може бути зроблено шляхом застосування добре відомі рівняння (правило трапеції):

Якщо інтервал [-π, π] ділиться на N - 1 інтервалів з вузлами -π = x1,
х2,. , , , ХN = π рівняння (3-58) можуть бути застосовані для кожного інтервалу окремо.
остаточна сума призводить до

Якщо ідентичні довжини h = xi+1−xi, i = 1 . . . N−1вибирають для інтервалів, ми Отримувати

Таким чином, ми можемо сформулювати загальне правило для обчислення дискретного коефіцієнтів від відповідного перетворення Фур'є-1D, які можуть бути використані для функціональної наближення вимірювань[z (x1) , . . . , z (xN)] = [z1, . . . , zN] в інтервалі
[-π, Π]. Очевидно, лінійна комбінація ортогональних тригонометричних функцій використовуваний. Нехай [z (x1) , . . . , z (xN)] = [z1, . . . , zN]бути вимірювання в [-π, π]. ці
Дані можуть бути апроксимовані за допомогою наступної лінійної комбінації ортогональних тригонометричні функції:

Для
відповідних коефіцієнтів і
![]() це
дає:
це
дає:

Для звичайного розтину інтервалу [-π, π], таких як (3-58 ??) рівнянь
(3-59) може бути спрощена

Примітка: припущення, що вимірювання приймати значення з інтервалу
[-π,
Π]
не є непереборною обмеженням. Якщо
![]()
[Z1,. , , , Zn] належать будь-якому інтервалі [а, Ь], ми можемо застосувати наступну трансформацію попереднє х-координат:

За допомогою цих нових координатах перетворення Фур'є для вимірювань
[z (x1) , . . . , z (xN)]=[z1, . . . , zN] може бути обчислена.
Нарешті, бек-перетворення повинні бути зроблені для того, щоб наблизити оригінальні вимірювання лінійної комбінації ортогональних функцій тригонометричними:

Кількість 2n + 1 коефіцієнтів Фур'є вибирається незалежно З числа N з даних вимірювань.
Тепер ми покажемо, перетворення Фур'є для простий набір з даних
Приклад 3.2.1.1. Приклад 3.2.1.5 Розглянемо наступні часові виміри від
Приклад
3.2.1.1:
![]()
Очевидно, що ці точки не належать інтервалу [-π, π], так до координат
перетворення (3-60) слід проводити:

С (* 0,1) в інтервалі [1, 10] перетворюється в [-π, π]. По-перше, ми п = 3 в
(3-59) і розрахувати сім коефіцієнти для аналітичного уявлення:

Завдяки рівновіддаленості х ми можемо використовувати рівняння (3-59?) І з N = 4 and x1


Аналогічно, ми маємо: а2 = -0,0667, Ь2 = -0,1732, а3 = -0,0333, b3 = 0, і
в
кінці кінців

після retransformation
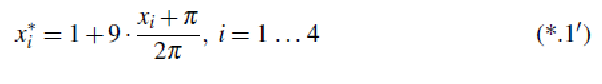
ми отримаємо аналітичну апроксимацію через перетворення Фур'є для даних вимірювань
(Див 3.16) .:

Детальніше про перевірку обгрунтованості перетворення Фур'є процедури можна знайти, наприклад, в Bracewell (1978) і Хеммінга (1973). Заміна синусоїдальні і косинусоидальной функції в ортогональній системі на інтервал [-π, π] з прикладу 3.2.1.4 іншими значимих функцій, визначених для повна речова вісь, що також ортогональні і виконувати деякі додаткові важливо математичні вимоги призводить до деяких корисним узагальнень перетворень Фур'є.
Сплески один з цих узагальнень, і тепер ми обговоримо основну ідею для
побудови 1D-сплесках.
