Курс теоретической механики 2007 (Рус)

точкам системы, получаем

Так как связи, наложенные на систему идеальны, то вторая сумма в выражении (174) равна нулю, и в результате будем иметь

n

∑(Fk , drk ) > 0 ,

k=1

что противоречит условию (170), так как перемещения точек drk (k = = 1,2,…,n) не противоречат наложенным связям, а значит, образуют возможное перемещение системы. Таким образом, наше предположение о том, что система пришла в движение неверно, и система находится в состоянии равновесия.

§4. Пример решения задачи с использованием принципа возможных перемещений

Задача. Плоский механизм, изображенный на рис.51, находится в состоянии равновесия под действием силы Q и пары сил с моментом

М. Необходимо найти момент пары, если Q = 2 кН , l1 = 2 м , l2 = 3 м , α = 30о.

Решение. Придаем механизму возможное перемещение, при котором кривошип О1А поворачивается на бесконечно малый угол δφ1 вокруг точки О1, а кривошип О1В − на угол δφ2 вокруг точки О2 . На этом перемещении сила Q и силы, образующие пару М, производят следующую работу

171

то δА и δВ пропорциональны расстояниям РА и РВ точек А и В от мгновенного центра вращения Р:

Из (176) и (177) находим

δφ2 = δφ1 l1 / (l2 tg α).

Подставляя это в (175), получаем

М = Q l1 cos2 α / sin α = 6 кНм.

§5. Определение реакций связей при помощи принципа возможных перемещений

В уравнении работ (170) принципа возможных перемещений реакции связей вообще не участвуют.

Поэтому для определения реакций при помощи принципа

возможных перемещений используется специальный метод:

1)отбрасываем связь, реакцию которой необходимо определить;

2)действие отброшенной связи заменяем силой, которая равна искомой реакции;

3)придаем системе с отброшенной связью возможное перемещение;

4)вычисляем сумму работ активных сил, включая добавленную, на этом перемещении;

5)из полученного уравнения находим добавленную силу и тем

самым определяем реакцию связи.

Продемонстрируем определение реакции на примере.

Задача. Определить реакцию шарнирно-подвижной опоры В составной рамы, изображенной на рис.52, Q1 = 20 кН , Q2 = 40 кН , М = = 40 кНм, а = 2 м, α = 45о. Связи, наложенные на раму, исключают возможность какого-либо перемещения.

Решение.

1. Отбрасываем шарнирно-подвижную опору В и получаем конструкцию, которая имеет возможность двигаться, т.е. механизм (рис.53).

172

2. Действие отброшенной связи заменяем силой RB , которая для механизма является активной.

Придаем механизму возможное перемещение, при котором левая часть рамы поворачивается на бесконечно малый угол δφ1 вокруг неподвижного шарнира А. При этом шарнир D, соединяющий две части рамы, получает перемещение δD, перпендикулярное отрезку AD, соединяющему его с центром вращения А. Шарнир С имеет воз-

Рис.52 можность перемещаться вдоль наклонной плоскости, поэтому воз-

можное перемещение δC точки С направлено вдоль нее. Восстанавливаем перпендикуляры к перемещениям δD и δC и на их пересечении находим положение мгновенного центра вращения, вокруг которого правая часть рамы поворачивается на бесконечно ма лый угол δφ2. Соотношение между δφ1 и δφ2 легко найти, выразив через них δD:

откуда находим

δφ2 = AD δφ1 = 2a δφ1 = 2δφ1 .

PD a

3. Составляем уравнение работ активных сил, включая RB , на этом перемещении

(RB a − Q1 2a) δφ1 − M δφ2 = 0.

Учитывая соотношения между δφ1 и δφ2, получаем

173

§6. Принцип Даламбера

Вектор J, равный по модулю произведению массы точки на ее ускорение и направленный противоположно ускорению, называется силой инерции точки:

Запишем основное уравнение динамики точки

n

ma = ∑Fk

k=1

иперенесем вектор ma направо. Учитывая (179), получаем

k=1

Так как силы, приложенные к материальной точке, образуют сходящиеся силы, а для них условием равновесия является равенство нулю главного вектора (см. §4 главы II части I), то (180) можно трактовать как условие равновесия. Таким образом,

если к силам, действующим на материальную точку добавить силу инерции этой точки, то полученная расширенная система сил будет удовлетворять условиям равновесия.

В этом и заключается принцип Даламбера для материальной точки.

Заметим, что сила инерции не относится к числу реально действующих на точку сил, т.е.

сила инерции материальной точки является фиктивной силой.

Она необходима для того чтобы уравнениям динамики точки придать форму уравнений статики.

Рассмотрим теперь механическую систему, на точки которой действуют внешние и внутренние силы (рис.54), и добавим к этим силам силы инерции материальных точек

Jk = − mk ak (k = 1,2,…,n).

В результате получается расширенная система сил, состоящая из подсистем {Fke , Fki , Jk }, у каждой из которых главный вектор и главный момент равны нулю. Следовательно, у всей расширенной

174

системы сил в целом главный вектор и главный момент равны нулю:

n

∑(Fke + Fki + Jk ) = 0,

n

∑[m0 (Fke ) + m0 (Fki ) + m0 (Jk )] = 0.

k=1

Таким образом,

если к силам, действующим на механическую систему добавить силы инерции точек системы, то полученная расширенная система сил будет удовлетворять условиям равновесия.

В этом и заключается принцип Даламбера для механической системы.

§7. Главный вектор и главный момент сил инерции

Векторные величины

Называются соответственно главным вектором и главным моментом относительно полюса О сил инерции.

Тогда (181) может быть записано так

Re + Ru = 0,

Из (182) получаем

Ru = − Re.

Из теоремы о движении центра масс следует, что Re = Mac . Тогда

175

т.е. главный вектор сил инерции точек механической системы

равен произведению массы системы на ускорение ее центра масс, взятому с противоположным знаком.

Таким образом, главный момент сил инерции точек

механической системы относительно любого полюса равен геометрической производной кинетического момента системы относительно этого полюса по времени, взятой с противоположным знаком.

Проектируя равенство (184) на ось z, получаем

Выясним к какому простейшему виду приводятся силы инерции твердого тела в различных случаях движения.

1. Поступательное движение. В этом случае тело относительно центра масс вращения не совершает. Поэтому LС = 0 и из (184) следует

MCu = 0 . По теореме Пуансо (§3 главы III части I)

при поступательном движении силы инерции эквивалентны одной силе, равной − Mac и приложенной в центре масс тела.

2.Вращение вокруг неподвижной оси z, проходящей через

центр масс. В этом случае очевидно ac = 0, т.е. Ru = 0. Вектор MCu

согласно (184) направлен вдоль оси вращения и его проекция на ось вращения определяется по формуле (185). Если использовать формулу Lz = Jz ω, то (185) принимает следующий вид

т.о. при вращении тела вокруг неподвижной оси, проходящей через

центр масс, силы инерции тела эквивалентны паре, лежащей в плоскости, перпендикулярной оси, и имеющей момент, равный произведению момента инерции тела относительно оси вращения

176

на его угловое ускорение, взятому с противоположным знаком.

3. Плоскопараллельное движение тела. Пусть тело имеет плоскость П симметрии и движется параллельно ей. Вследствие симметрии главный вектор сил инерции параллелен плоскости П, а главный момент относительно центра масс перпендикулярен этой плоскости. Если выбрать в качестве центра приведения сил инерции центр масс тела, то окажется , что силы инерции эквивалентны силе, приложенной в центре масс и равной − Mac , а также паре сил, лежащей в плоскости симметрии и имеющей момент равный −Jzε

(ось z проходит через центр масс перпендикулярно плоскости симметрии).

§8. Определение динамических реакций

Продемонстрируем применение принципа Даламбера при решении задач. Наиболее часто он используется при определении динамических

реакций.

Задача. Однородный стержень АВ длиной l и массой М прикреплен при помощи шарнира А к вертикальному валу, вращающемуся с

2 h = 2 l cos α от оси х. По величине эта равнодействующая равна

33

177

главному вектору сил инерции

Fu = Ru = Mac = Mω2 l sin α. 2

Плоская система сил P, RB , RAx , RAy , Fu удовлетворяет условиям равновесия, в частности, сумма моментов сил относительно оси z , перпендикулярной плоскости чертежа и проходящей через точку А,

Заметим, что

ω= πn = 20,94 с−1. 30

Тогда натяжение нити равно:

T = RB = 759,4 Н,

что больше статического натяжения нити (т.е., когда стержень не вращается) в 26,8 раз.

§9. Общее уравнение динамики (принцип Даламбера−Лагранжа)

Рассмотрим механическую систему, подчиненную идеальным, стационарным, геометрическим, удерживающим связям. Согласно принципу Даламбера, если к действующим на эту систему активным силам Fk и реакциям связей Rk добавить силы инерции точек Jk , то полученная расширенная система сил удовлетворяет условиям равновесия. Согласно принципу возможных перемещений, таким условием равновесия является равенство нулю суммы элементарных работ расширенной системы активных сил (в их число включаются и силы инерции) на любом возможном перемещении системы. Таким образом, в результате совместного применения принципа Даламбера и принципа возможных перемещений (принципа Лагранжа) получаем следующее утверждение (принцип Даламбера−Лагранжа):

при движении механической системы, подчиненной идеальным, стационарным, геометрическим, удерживающим связям, сумма

178

элементарных работ активных сил, приложенных к точкам системы, и сил инерции этих точек на любом возможном перемещении системы равна нулю:

k=1

Уравнение (187) носит название общего уравнения динамики.

Рассмотрим пример использования общего уравнения динамики

при решении задач.

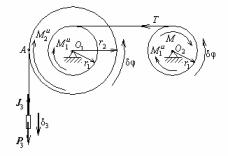
Задача. На два одинаковых барабана радиуса r1 и массой т1 намотана веревка так, как показано на рис.56. К одному из них приложен вращающий момент М, а другой жестко скреплен с колесом радиуса r2 и массой т2 . На колесо намотана веревка, к концу которой подвешен груз массой т3 . Определить угловое ускорение барабанов, а также натяжение веревки, намотанной на барабаны, если r1 = 1 м, r2 = 2 м, М = 2 кНм , т1 = 20 кг , т2 = 40 кг , т3 = 40 кг. Барабаны и колесо

(заметим, что ε1 = ε2 = ε , так как радиусы барабанов, через которые переброшена веревка, одинаковы, колесо и барабан соединены жестко). Величина силы инерции груза определяется по формуле

179

J3 = m3a3 ,

где а3 − ускорение груза. Заметим, что ускорение груза равно касательному ускорению точки А на ободе колеса, т.е. а3 = ε r2 . Таким образом,

барабаны поворачиваются на бесконечно малый угол δφ, а груз получает бесконечно малое перемещение δ3 . Очевидно,

На основании принципа Даламбера−Лагранжа сумма элементарных работ вращающего момента М , веса груза Р3 , пар сил с моментами

M uj ( j = 1,2) и силы инерции груза J3 на вышеуказанном возможном перемещении должна быть равна нулю:

Принимая во внимание (188) − (190), записываем (191) в следующем виде:

Рассмотрим теперь расширенную систему активных сил, приложенных к правому барабану: M, M1u ,T (Т − натяжение веревки).

Их элементарная работа на бесконечно малом повороте барабана равна нулю

(T r1 − M − M1u )δφ = 0 . Отсюда определяем

180