
Курс теоретической механики 2007 (Рус)
.pdf
Г Л А В А V
ВРАЩЕНИЕ ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ. ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
§ 1. Углы Эйлера. Уравнения вращения тела вокруг неподвижной точки
Рассмотрим движение тела, имеющего неподвижную точку О относительно неподвижной системы координат Оxоyоzо, начало которой находится в неподвижной точке
|
тела (рис.40). Жестко свяжем с телом |
|||||||
|
подвижную |
систему |
координат |
Оxyz. |
||||
|
Линия |
ОК |
пересечения |
плоскостей |
||||
|
xоОyо |
и xОy носит |
название |
линии |
||||
|
узлов. |
|
|
|
|
|
|
|
|
Введем следующие углы: |
|
|
|
||||
|
угол |
между |
осями |
Ozo |
и |
Oz |
||
|
называется |
углом |
нутации |
и |
||||
|
обозначается буквой θ; |
|
|
|
|
|||
|
угол |
между осью Охо и линией уз- |
||||||
Рис.40 |
лов называется углом прецессии и обоз- |
|||||||
|
начается буквой ψ; |
|
|
|
|
|
||
угол между линией |
узлов и осью Ох |
называется |
углом |
|||||
собственного вращения и обозначается буквой φ.
Углы нутации θ, прецессии ψ и собственного вращения φ
называются углами Эйлера. Можно доказать, что углы Эйлера однозначно определяют положение подвижной системы координат Оxyz относительно неподвижной Оxоyоzо , а значит и
положение тела относительно неподвижной системы координат. Поэтому уравнения вращения твердого тела вокруг
неподвижной точки имеют следующий вид: |
|
θ = f1 (t), ψ = f2 (t), φ = f3 (t), |
(89) |
так как при подстановке любого времени в правые части (89) получаем значения углов θ, ψ, и φ, которые однозначно определят положение тела в этот момент времени.
101
§ 2. Теорема Эйлера-Даламбера
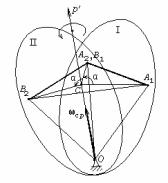
Теорема. Перемещение тела, имеющего неподвижную точку, из положения I, которое оно занимало в момент времени t, в положение II, занимаемое им спустя промежуток времени t,
можно осуществить вращением вокруг некоторой неподвижной оси Op’, проходящей через неподвижную точку O, на некоторый конечный угол Δα.
Ось Op’ называется осью конечного вращения, а угол Δα − углом
конечного вращения.
Доказательство. Выберем некоторую точку тела А1 в начальном положении I. В результате перемещения она займет положение А2 в конечном положении тела II. В этом месте пространства находилась некоторая точка тела В1 из положения I. После перемещения она займет положение В2. Если соединить точки А1 и В1 отрезком А1В1 , то в результате перемещения он займет положение А2В2 , причем начало А1 отрезка А1В1 переместится в точку А2 , т.е. в его конец (рис.41). Если соединить точки А1 и В2 отрезком прямой, то образуется треугольник
Рис.41 А1В1В2. Проведем из неподвижной точки О перпендикуляр к плоскости треугольника А1В1В2 и обозначим точку пересечения перпендикуляра с
этой плоскостью буквой С. Соединим точки А1, В1 и В2 с неподвижной точкой О отрезками прямых ОА1, ОВ1 и ОВ2.
Заметим, что
А1В1 = В1В2, |
(90) |
так как это различные положения одного и того же отрезка А1В1 твердого тела.
Кроме того, ОА1 = ОВ1, потому что это два положения отрезка ОА1. Аналогично ОВ1 = ОВ2. Таким образом, ОА1 = ОВ1 = ОВ2. Получается, что к плоскости треугольника А1В1В2 проведено три равные наклонные. Следовательно, равны и их проекции, т.е.
СА1 = СВ1 = СВ2. |
(91) |
102

Из (90) и (91) вытекает, что треугольники А1СВ1 и В1СВ2 равны, так как три стороны одного равны трем сторонам другого. Это значит, что
А1СВ1 = В1СВ2 . |
(92) |
Обозначим величину этих равных углов через α. Если теперь повернуть тело из положения I вокруг оси Оp’ (проходящей через точку С) на угол α (направление вращения показано на чертеже), то точка А1 перейдет в точку А2, а точка В1 – в точку В2, причем точка О останется на месте. Это значит, что при этом тело из положения I перейдет в положение II, что и требовалось. Теорема доказана.
Введем для вращения тела из положения I в положение II вектор средней угловой скорости ωср за промежуток времени t следующим образом: направим его вдоль оси вращения в соответствующую сторону (см. §5 главы II), а величину определим так:
|ωср| = | |
α |
| |
(93) |
|
|||
|
t |
|
|
§ 3. Ось мгновенного вращения. Мгновенная угловая скорость. Первая формула Эйлера
Пусть теперь t → 0. При этом ось конечного вращения Оp’ будет поворачиваться вокруг точки О. Предельное положение Ор оси конечного вращения Op' при стремлении к нулю промежутка
времени называется осью мгновенного вращения.
Средняя угловая скорость ωср, будучи направленной вдоль оси конечного вращения, в пределе будет направлена вдоль оси
мгновенного вращения. Величина же ее |ωср| = | α | будет стремиться t
вообще говоря к некоторому конечному пределу, так как α стремится к нулю при t → 0.
Предел ω, к которому стремится средняя угловая скорость ωср при стремлении к нулю промежутка времени, называется мгновенной угловой скоростью. Она направлена вдоль оси мгновенного вращения Ор в ту сторону, откуда видно вращение
тела вокруг этой оси против часовой стрелки, и по величине равна
|ω| = lim | |
α |
|. |
(94) |
|
|||
t→0 |
t |
|
|
103

Таким образом, можно представлять, что в каждый момент времени тело, имеющее неподвижную точку, совершает мгновенное вращение вокруг оси мгновенного вращения ОР с угловой скоростью, равной мгновенной угловой скорости ω. Поэтому возможно использование первой формулы Эйлера (§5 главы II) и для нахождения скоростей точек тела, имеющего одну неподвижную точку:
V = [ω, r] |
(95) |
Рис.42
§ 4. Движение свободного твердого тела (произвольное движение тела). Уравнения движения
|
Пусть на движение твердого |
|||
|
тела относительно неподвижной |
|||
|
системы координат Оxоyоzо не |
|||
|
наложено никаких ограничений. |
|||
|
Выберем некоторую точку А тела |
|||
|
и проведем через нее оси |
|||
|
подвижной |
системы координат |
||
|
Аx1y1z1 |
параллельно |
осям |
|
|
неподвижной системы координат |
|||
|
(рис.43). |
В |
дальнейшем |
|
|
движении |
они |
|
должны |
|
оставаться |
параллельными не- |
||
|
подвижным осям. |
|
|
|
|
Рассмотрим теперь движение |
|||
Рис.43 |
свободного тела как сложное. |
|||
Переносное движение, т.е. движение подвижной системы координат Аx1y1z1 относительно неподвижной Оxоyоzо, является поступательным, так как оси подвижной системы перемещаются параллельно своему первоначальному положению.
Относительное движение, т.е. движение тела относительно системы Аx1y1z1 является вращением вокруг неподвижной точки, так как точка А тела остается неподвижной в этой системе координат.
104

Таким образом, движение свободного тела разложено на поступательное и вращение вокруг неподвижной точки.
Точка А тела, являющаяся началом подвижной системы координат, называется полюсом разложения свободного движения на поступательное и вращательное.
Очевидно, уравнениями движения свободного тела будут уравнения переносного и относительного движений.
Так как поступательное движение подвижной системы определяется движением начала координат, то уравнениями переносного движения является уравнения движения точки А.
Для записи уравнений относительного вращения необходимо ввести еще одну систему координат Аxyz, жестко связанную с телом. Ее положение относительно системы Аx1y1z1 определяется углами Эйлера, задание которых как функций времени дает уравнения относительного движения.
Таким образом, уравнения свободного движения тела имеют следующий вид:
x0A = f1 (t), y0A = f2 (t), z0A = f3 (t), θ = f4 (t), ψ = f5 (t), φ = f6 (t). (96)
Угловая скорость относительного вращения не зависит от выбора полюса разложения.
Действительно, возьмем два различных полюса разложения А1 и А2 и соответственно две подвижные системы координат
А1x1y1z1 и А2x2y2z2 , параллельные осям неподвижной системы.
Кроме того, проведем через каждый из полюсов оси систем координат А1xyz и А2x/y/z/, жестко связанные с телом, параллельно
Рис.44 друг другу (рис.44).
В результате углы Эйлера в
полюсах окажутся равными:
θ1 = θ2 , ψ1 = ψ2 , φ1 = φ2 .
Это значит, что вращение тела относительно полюсов А1 и А2 идентично, а следовательно, в каждый момент времени мгновенные
105

угловые скорости вращения ω1 и ω2 геометрически равны.
§ 5. Вторая формула Эйлера
Пусть А – полюс разложения свободного движения тела на поступательное и вращательное, а В − произвольная точка тела (рис.45). Проведем радиус-векторы точек А и В из начала неподвижной системы координат, а также
вектор AB , соединяющий эти точки. Из рисунка следует, что
rB = rA + AB . (97) Дифференцируя равенство (97) по времени, получаем
|
V |
|
= V |
|
+ |
d AB |
. (98) |
||
B |
A |
dt |
|||||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
||||||
Но |
d AB |
есть скорость VBA |
|||||||
|
|||||||||
|
dt |
|
|
|
|
|
|
||
точки В в относительном враРис.45 щении тела вокруг точки А..
Таким образом, (98) запи-
сывается так:
VB =VA +VBA , |
(99) |
т.е. скорость любой точки свободного твердого тела равна
скорости произвольно выбранного полюса, геометрически сложенной со скоростью этой точки в относительном вращении тела относительно полюса.
Используя формулу (95) параграфа 3 (т.е. первую формулу Эйлера), VBA может быть записано так:
|
|
|
|
VBA = [ω, AB] , |
(100) |
||
а тогда (99) представится в следующем виде:
|
|
|
|
VB = VA +[ω, AB] . |
(101) |
||
Формула (101) (или совместно формулы (99) и (100)) и носит название
106
второй формулы Эйлера.
Следствия.
1)Проекции скоростей точек тела на направление вектора
ωравны.
Действительно, вектор VBA перпендикулярен вектору ω как одному из сомножителей векторного произведения (100), и поэтому его проекция на направление вектора ω равна нулю. Проектируя (99) на это направление, получаем
прω VB = прω VB .
Совершенно аналогично доказывается следствие
2) Проекции скоростей двух точек тела на ось, проходящую через эти точки равны.
107
Ч А С Т Ь III. Д И Н А М И К А
_____________________________________________________________
Г Л А В А I
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
§1. Введение в динамику. Законы динамики
Введем некоторые определения.
Инертностью называется свойство материальных тел быстрее или медленнее менять скорость своего движения под действием приложенных сил. Если при действии одинаковых сил изменение скорости одного тела происходит медленнее, чем другого, то первое тело считается более инертным, чем второе.
Количественной мерой инертности тела является физическая величина, называемая его массой.
Если расстояние, на которое перемещается тело очень велико по сравнению с размерами тела, то при изучении движения размерами тел можно пренебречь. Таким образом возникает понятие о материальной точке.
Материальной точкой называется тело, не имеющее размеров, но обладающей не равной нулю массой.
Материальная точка называется изолированной, если на нее не действуют силы.
В основе динамики лежат законы, установленные путем обобщения громадного количества опытов и наблюдений над движением тел и проверенные многовековой практикой человечества. Впервые систематически законы динамики были изложены И.Ньютоном в книге «Математические начала натуральной философии», вышедшей в 1687 году.
Первый закон (закон инерции Галилея-Ньютона). Существует по крайней мере одна система отсчета, относительно которой любая изолированная материальная точка движется равномерно и прямолинейно либо находится в состоянии покоя.
Такая система отсчета называется инерциальной. Как показывает многолетний опыт, при изучении движения планет и других тел Солнечной системы инерциальной можно считать систему отсчета, начало которой находится в центре Солнца, а оси направлены на так
108

называемые неподвижные звезды. При решении многих технических задач инерциальной можно считать систему отсчета, жестко связанную с Землей.
Второй закон. Сила, действующая на материальную точку, сообщает ей ускорение, которое в инерциальной системе отсчета пропорционально величине силы и имеет направление, совпадающее с направлением силы.
Математически этот закон выражается в виде равенства
ma = F, |
(1) |
где m – масса точки, а – ее ускорение, F – сила, действующая на точку.
Третий закон (закон независимости действия сил). Если на материальную тоску действует несколько сил, то ее ускорение в инерциальной системе отсчета равно геометрической сумме ускорений, вызываемых каждой из сил в отдельности, т.е.
n |
|
a = ∑ak , |
(2) |
k=1
где аk - ускорение, вызванное силой Fk (k=1,2,…,n).
По предыдущему закону ak = Fk / m . Подставляя это в (2), получа-
ем
n |
|
ma = ∑Fk . |
(3) |
k=1
Обычно третий закон записывают в виде равенства (3). Это равенство еще носит название «основное уравнение динамики
материальной точки».
Четвертый закон (закон равенства действия и противодействия). Любое взаимодействие двух материальных
точек осуществляется при помощи двух прямопротивоположных сил.
Напоминаем, что две силы называются прямопротивоположными, если они лежат на одной прямой, направлены в противоположные стороны и равны по величине (рис.1).
Рис.1
109
Пятый закон (закон всемирного тяготения). Любые две материальные точки притягиваются друг к другу силами, прямо пропорциональными произведению их масс и обратно пропорциональными квадрату расстояния между ними:
F |
= F |
= γ |
m1m2 |
. |
(4) |
|
|||||
1 |
2 |
|
r 2 |
|
|
|
|
|
|
||
Здесь m1 и m2 – массы точек, r – расстояние между ними, γ – гравитационная постоянная.
§2. Основные задачи динамики материальной точки. Решение первой задачи
Косновным задачам динамики материальной точки относятся
1)первая задача: задано движение точки, необходимо найти силу, действующую на точку;
2)вторая задача: заданы силы, действующие на точку, необходимо найти закон движения точки.
В качестве примера решения первой задачи динамики точки
рассмотрим |
проблему определения зависимости |
между весом |
|||
материальной точки и ее массой. |
|
|
|
|
|
|
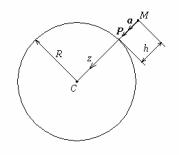
Пусть |
некоторая |
материальная |
||
|
точка массы m свободно падает без |
||||
|
начальной |
скорости |
с некоторой |
||
|
высоты h на поверхность Земли |
||||
|
(рис.2). Можно показать, что сила Р |
||||
|
гравитационного притяжения к Земле |
||||
|
направлена к центру Земли, а |
||||
|
величина ее может быть вычислена |
||||
|
по формуле (4) в предположении, что |
||||
|
масса Земли сосредоточена в ее |
||||
|
цетре: |
|
|
|
|
|
Рис.2 |
P = γ |
mM |
. |
|
|
|
||||
|
|
|
(R + h)2 |
||
Здесь М – масса, а R – радиус Земли. Будем полагать, что высота h, с которой падает точка, гораздо меньше радиуса Земли, и поэтому R + h с большой степенью точности равно R . Тогда
P = γ |
mM |
. |
(5) |
|
|||
|
R2 |
|
|
Запишем основное уравнение динамики точки
110
