
- •Передаточные функции типовых сар по каналам возмущения и задания
- •Оценка работы систем автоматического управления
- •Лекция №6
- •Анализ линейных непрерывных сар: устойчивость сар
- •Общее понятие устойчивости динамической системы. Особенности устойчивости линейных сар
- •Определение устойчивости сар прямыми методами. Виды неустойчивости
- •(Колебательный характер) (апериодический характер)
- •Лекция №7 Частотные критерии устойчивости
- •Лекция №8 Области устойчивости сар в пространстве параметров регулятора и объекта
- •Лекция №9 анализ качества сар Ошибки стабилизации и воспроизведения сар
- •Качество переходных процессов в сар при ступенчатых входных воздействиях
- •Прямые показатели качества переходных процессов (переходных характеристик) и их определение
- •Регламентные зоны переходного процесса
- •Лекция №10 Интегральные показатели качества
- •Статизм и астатизм типовых сар
- •Понятие о грубости и чувствительности сар
- •Лекция №11 синтез сар Задача синтеза в общей постановке и ее декомпозиция
- •Типичные критерии оптимальности
- •Типичные ограничения
- •Декомпозиция задачи синтеза.
- •Параметрический синтез типовых сар
- •Критерии, используемые в инженерных методиках синтеза
- •Методика расчета настроечных параметров регуляторов Копеловича а.П. (с использованием формул)
- •Методика расчета настроечных параметров регулятора Копеловича а.П. – Клюева а.С. (с использованием номограмм)
- •Корректировка параметров регулятора на работающем объекте
(Колебательный характер) (апериодический характер)
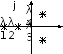
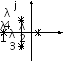
Рис. 6.3
Расположение полюсов на мнимой оси означает, что система находится на границе устойчивости.
В том случае, если неустойчивость обусловлена положительностью действительной части (αi) комплексной пары корней, то она имеет колебательный характер и называется колебательной неустойчивостью. Такая неустойчивость вызывается чрезмерно интенсивным воздействием регулятора на объект. Это обуславливается несоответствием установленных значений настроечных параметров регулятора свойствам (параметрам) объекта. Для устранения колебательной неустойчивости необходимо перенастроить регулятор.
Если неустойчивость обусловлена положительностью действительного корня, то она имеет апериодический характер и называется апериодической неустойчивостью. Апериодическая неустойчивость определяется наличием в системе положительной обратной связи. Устранить такую неустойчивость изменением параметров регулятора невозможно. Для простейших систем апериодическая неустойчивость всегда вызвана ошибкой в установленном знаке обратной связи (неправильном «направлении» воздействия регулятора при возникновении ошибки регулирования). Для устранения такой неустойчивости надо установить правильный знак обратной связи.
Системы, в которых изменением параметров регулятора невозможно добиться устойчивости, называются структурно неустойчивыми. Для обеспечения устойчивости таких систем нужно изменять структуру УУ (в частности – знак обратной связи).
Важно: для систем с запаздыванием оценка устойчивости САР по корням характеристического уравнения напрямую невозможна. Это связано с тем, что ДУ с отклоняющим аргументом теоретически имеет бесчисленное множество корней.
Исключить из передаточной функции системы, точнее из собственного оператора, трансцендентную передаточную функцию чистого запаздывания можно, разложив эту передаточную функцию в дробно-рациональный ряд Паде. На практике чаще пользуются рядом Паде второго порядка:
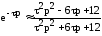 .
.
Лекция №7 Частотные критерии устойчивости
Частотные критерии дают возможность работать с системами, имеющими запаздывание без разложения запаздывания в упрощающие ряды.
А) критерий Михайлова
Пусть САР описывается однородным ДУ Qc(p).у = 0. Собственный оператор системы Qc(p) переведем в частотную область, для этого необходимо применить преобразование Фурье (формально заменить р на jω):
Qc(p)
Qc(j)
=
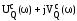 .
.
Формулировка критерия: система устойчива, если годограф Qc(jω)
(годограф
Михайлова) начинается на действительной
положительной полуоси и огибает против
часовой стрелки начало координат,
последовательно проходя n квадрантов.
В том случае, если
система имеет запаздывание, то ее
годограф может представлять собой
раскручивающуюся спираль, которая
последовательно проходит бесконечное
число квадрантов.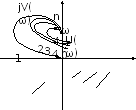
Рис. 7.1. Примеры годографов Михайлова САР 4-го порядка:
1 – САР устойчива; 2 – САР на границе устойчивости; 3, 4 – САР неустойчива

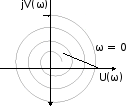
Рис.
7.2. Примеры годографов Михайлова
устойчивых систем различного
порядка Рис.
7.3. Пример годографа Михайлова
устойчивой САР с
запаздыванием
Для оценки устойчивости точный вид годографа Михайлова знать необязательно, а необходимо знать точки пересечения с его осями и последовательность их расположения, т.е. значения ω, которым они соответствуют. Для нахождения этих точек можно воспользоваться двумя условиями:
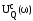 = 0 – условие
пересечения с осью V(ω);
= 0 – условие
пересечения с осью V(ω);
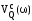 = 0 – условие
пересечения с осью U(ω);
= 0 – условие
пересечения с осью U(ω);
(когда оба условия выполняются при одинаковых значениях ω, то система находится на границе устойчивости).
Процедура нахождения точек:
1. Решая уравнение, описывающее условие пересечения с одной из осей, определяем значения частот, соответствующих точкам пересечения, как корни этого уравнения.
2. Подставляем значения найденных частот в другое выражение, найдем точки пересечения с осью, соответствующие этим частотам.
Б) критерий Найквиста
Позволяет судить
об устойчивости замкнутой системы по
годографу (АФЧХ) соответствующей
разомкнутой системы с передаточной
функцией: Wpc(p)
=
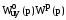 .
Это произведение передаточных функций,
входящих в замкнутый контур САР.
.
Это произведение передаточных функций,
входящих в замкнутый контур САР.
В частотной области она принимает вид:
Wpc(j)
=
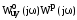 =Apc()
=Apc()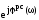 =Upc()
+ jVpc().
=Upc()
+ jVpc().
Важно: Apc()
=
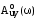 Ap();
pc()
=
Ap();
pc()
=
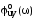 + p().
+ p().
Индекс «о» обозначает характеристику объекта, «р» – регулятора, «рс» – разомкнутой системы.
Формулировка критерия (для случая, когда САР в разомкнутом состоянии устойчива): замкнутая САР устойчива, если годограф (АФЧХ) разомкнутой системы не охватывает точку с координатами (–1; j0).
Примеры:
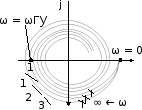
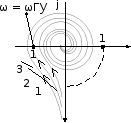
Рис.
7.5. Примеры АФЧХ астатических
разомкнутых систем
первого порядка. Соответствующая
замкнутая САР: 1
– устойчивая;
2 – на
границе устойчивости;
3 – неустойчивая
Рис.
7.4. Примеры АФЧХ статических
разомкнутых систем. Соответствующая
замкнутая САР: 1
– устойчивая; 2 – на границе устойчивости;
3 – неустойчивая
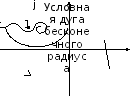
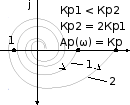
Рис.
7.6. Пример АФЧХ астатической разомкнутой
системы второго порядка и
построения условной дуги для определения
охвата им точки (–1; j0) Рис.
7.7. Пример изменения АФЧХ разомкнутой
САР со статическим объектом
и П- регулятором при изменении
коэффициента передачи
регулятора
На основе критерия Найквиста вводят понятие запасов устойчивости САР по модулю и по фазе. Коэффициент запаса устойчивости по модулю САР показывает насколько должна измениться длина радиус-вектора АФЧХ, т.е. Ac(ω) при неизменном c(ω) = –π, чтобы система вышла на границу устойчивости.
Запас устойчивости по фазе показывает, насколько должна измениться фаза АФЧХ при неизменной, равной единице, ее амплитуде – Арс(ω) = 1 (длине радиус-вектора) чтобы система вышла на границу устойчивости.
Запасы устойчивости
САР по амплитуде (модулю) АГУ
и ГУ
по фазе, можно пересчитать в запасы ее
устойчивости по коэффициенту передачи
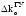 и времени запаздывания объекта
и времени запаздывания объекта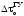 :
: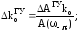
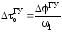 ,
,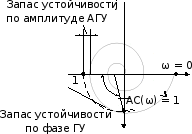
Рис. 7.8. Иллюстрация определения
запасов устойчивости
где – – значение частоты, при которой фазовый сдвиг в разомкнутой САР равен –;
1 – значение частоты, при которой значение АЧХ разомкнутой САР равно 1;
А(–) – значение АЧХ разомкнутой САР при частоте = –.
