
Матфизика Мурга Е.В
.pdf
X 0 C1 0,
а при х =
X С2 sin 0 .
Оскільки варіант С2=0 дає (з урахуванням С1=0) тривіальне рішення, залишається
sin 0 ,
тобто |
k |
k 1, 2,... . |
Значить, якщо k , то існують нетривіальні рішення задачі
(3.7)-(3.8) вигляду
k Xk x Ck sin x.
Знайдені значення називаються власними значеннями для даної крайової задачі, а функції Xk(x) – власними функціями.
Помітимо, що знайдені власні функція ортогональні на інтервалі 0, . Тепер слід відшукати функцію T(t). Функція Tk(t)
відповідна власному значенню k , задовольняє рівнянню
41

k a 2
Tk t Tk t 0,
загальне рішення якого має вигляд:
Tk t Ak |
cos |
k a |
t Bk |
sin |
k a |
t, |
|
|
|||||
|
|
|
|
|
||
Підставляючи знайдені функції Xk(t) і Тk(t) формулу (3.4),
можна отримати рішення рівняння (3.1), що задовольняють крайовим
умовам (3.2):
|
|
k a |
|
|
k a |
|
|
|
k |
|
|
|
||
uk x,t ak cos |
|
t bk |
sin |
|
t |
sin |
|
|
x. |
|
(3.9) |
|||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тут введені позначення |
a C A, |
b |
k |
C |
k |
B |
k |
, |
k 1,2,3,... |
|||||
|
|
|
k |
k k |
|
|
|
|
|
|
||||
Рішення (3.9) |
називаються власними функціями задачі (3.1)- |
|||||||||||||
(3.3), відповідні їм коливання струни – власними коливаннями.
Тепер доцільно перейти і заключній частині методу Фур’є: за
допомогою власних функцій побудуємо рішення, що задовольняє початковим умовам (3.2). Для цього візьмемо суму рішень (3.9), яка через лінійність і однорідність рівняння (3.1) також буде його рішенням:
|
|
|
k a |
|
k a |
|
k |
|
||
u x,t |
|
|
(3.10) |
|||||||
ak |
cos |
|
t bk |
sin |
|
t sin |
|
x, |
||
|
|
|
||||||||
k 1 |
|
|
|
|
|
|
|
|
||
42
Якщо цей ряд, а також що виходять з нього двократним
диференціюванням по x і по t, сходяться рівномірно на 0, , то функція (3.10) задовольняє рівнянню (3.1) і крайовим умовам (3.3).
Залишилося підібрати довільні постійні ak і bk так, щоб
задовольнити початковим умовам (3.2). При t=0 із співвідношення
(3.10) легко отримати
|
|
k |
|
|
|
u x,t ak |
sin |
x x . |
(3.11) |
||
|
|||||
k 1 |
|
|
|
||
Для задоволення другої початкової умови необхідно продиференціювати ряд (3.10) по t:
|
u |
|
|
|
|
k a |
|
|
|
|
k a |
k a |
k |
|
|
|||||||||
|
|
|
|
ak |
sin |
|
|
t bk |
cos |
|
|
|
t |
|
|
sin |
|
x |
|
|
||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
t |
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
і підставити t=0: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
u |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
k a |
bk sin |
x x . |
|
|
(3.12) |
|||||||||||||
|
|
|
t |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
t 0 |
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Формули |
(3.11) |
і |
(3.12) означає, |
що |
числа |
ak і |
k a |
bk є |
||||||||||||||||
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
коефіцієнтами розкладання функцій |
x |
|
і x |
в ряд Фур’є по |
||||||||||||||||||||
синусах в інтервалі 0, |
, тобто |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
43
|
2 |
|
|
|
k |
|
|
|
|
|
|
|
||
ak |
x sin |
xdx; |
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
0 |
|
|
|
|
|
|
|
k 1,2,... |
|
(3.13) |
|
|
|
|
2 |
|
|
|
k |
|
||||||
|
|
|
|
|
|
|
|
|
||||||
bk |
|
0 |
(x)sin |
|
|
|
xdx. |
|
|
|
|
|||
k a |
|
|
|
|
|
|
|
|||||||
Таким чином, при реалізації методу Фур’є для задачі (3.1)-(3.3) |
||||||||||||||
треба розкласти початкові дані x і |
x в ряд Фур’є по синусах |
|||||||||||||
на 0, . |
|
|
|
|
|
|
|
|
|
|
|
|
||
Підставляючи вирази для коефіцієнтів аk і bk |
в ряд |
(3.10), |
||||||||||||
остаточно знайдемо рішення поставленої задачі. |
|
|
|
|||||||||||
Зауваження: важливо звернути увагу на умови, що |
||||||||||||||
накладаються на функції x |
і x |
, щоб забезпечити законність |
||||||||||||
двократного почленного диференціювання ряду (3.10) по x і no t. |
|
|||||||||||||
Приклад |
|
1. Знайти |
|
коливання струни із закріпленими |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
кінцями |
х=0 і |
х= , |
|
|
|
|
|
|
|
|
|
|
|
|
якщо |
|
початкові |
|
|
|
|
|
|
|
|
|
|
|
|
швидкості |
точек рівні |
||
|
|
|
|
|
|
|
|
|
|
|
нулю, |
а |
початкове |
|
|
|
|
|
|
|
|
|
|
|
|
відхилення має форму |
|||
|
|
|
|
|
|
|
|
|
|
|
трикутника |
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
вершиною |
у |
точці |
|
|
|
|
|
|
|
|
|
|
|
|
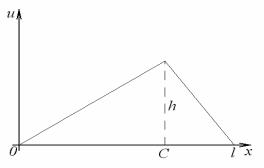
(С,h) (рисунок 3.1). |
|||
|
|
|
|
|
|
|
|
|
|
|
В момент |
t 0 |
||
|
|
Рисунок 3.1 |
|
|
|
|
струна займає |
положення, |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
44
зображене на рис. 3.1. Опишемо положення струни аналітично.
|
|
|
|
Для 0 x C |
|
є |
u |
|
h |
x |
|
|
|
(рівняння прямої, що проходить |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
через |
початок координат, |
кутовий |
|
|
|
|
коефіцієнт |
|
h |
|
). |
|
|
Для |
C x |
|||||||||||||||||||||||||||||||||
|
|
|
C |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
складемо рівняння прямої, що проходить через точки |
,0 |
і C,h : |
||||||||||||||||||||||||||||||||||||||||||||||
|
u 0 |
|
|
x |
, звідки |
|
|
|
|
|
|
|
|
|
|
|
u |
h |
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
h 0 |
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Задача приводиться до інтеграції рівняння |
|
|
2u |
a2 |
2u |
|
за |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x2 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|||||||
нульових крайових умов з початковими умовами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x, |
|
|
0 x C, |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
u x,0 x |
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h , |
C x . |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Щоб знайти ak , bk |
слід використовувати формули (3.13) |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
2 |
|
C |
h |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
ak |
|
u x,0 sin |
xdx |
|
|
xsin |
xdx |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
2 |
|
|
|
h |
x sin |
k |
|
|
|
|
|
|
|
2h |
|
|
|
|
|
k |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
xdx |
xsin |
xdx |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
C |
|
C |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2h |
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x sin |
xdx. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
C l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Інтеграли беруться по частинах
45
C |
|
|
k |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
k |
|
|
|
|
C |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
C |
|
|
||||||||||||||||||||||||
xsin |
xdx |
|
cos |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
x |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
k C |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
k C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
k |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
k |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
x sin |
xdx |
|
cos |
x |
|
|
|
|
|
|
|
|
|
|
sin |
|
x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
k |
|
|
|
|
|
|
|
|
C |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
k |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
C. |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Отже, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
2h |
cos |
k C |
|
|
|
|
|
2 l |
|
|
sin |
k C |
|
|
2h |
cos |
k C |
|
||||||||||||||||||||||||||||||||||||||||||||||||
k |
|
|
|
k2 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
sin |
|
k C |
|
|
|
|
|
|
|
|
2h 2 |
|
|
|
|
|
|
sin |
|
k C |
, |
|
|||||||||||||||||||||||||||||||||||
|
|
|
k2 2 C |
|
|
|
|
|
|
|
k2 2C C |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
оскільки початкова |
|
швидкість |
|
|
|
відсутня, |
|
|
|
|
|
коефіцієнти |
|
bk 0 . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Залишилося підставити знайдені значення ak і bk у формулу (3.10). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Відповідь: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
2h |
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
k C |
|
|
|
|
|
k x |
|
|
|
|
|
|
|
k at |
|
|
|
||||||||||||||||||||||||||
u x,t |
|
|
|
|
|
|
|
|
|
|
|
sin |
sin |
cos |
. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
C C |
|
|
k 1 |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Приклад 2. Однорідна струна завдовжки l натягнута між
точками x=0 і x=l. Початкова форма струни задається функцією
46
x Asin n x, початкова швидкість рівна нулю. Визначити
відхилення u x,t .
По формулах (3.13) слід знайти коефіцієнти ak і bk.
Коефіцієнти bk 0 , оскільки відсутня початкова швидкість Початкове положення струни співпадає з графіком однієї з власних функцій.
Тому крім всіх коефіцієнтів bk, звертаються в нуль і всі коефіцієнти ak
при k n, оскільки власні функції ортогональні.
|
|
2 |
|
n x |
|
|
an |
A |
sin2 |
dx A. |
|||
|
|
|||||
|
|
|
0 |
|
||
Значить, з ряду (3.10) залишається один доданок
u x,t Asin n a tsin n x.
Рішення можна записати у вигляді
u x,t A x sin n a t,
де A x Asin n x, амплітуда коливання, залежна від абсциси точки
струни. Всі точки струни скоюють гармонійні коливання з однією і
тією ж частотою n a . При цьому всі точки струни одночасно
47
досягають свого максимального відхилення і одночасно проходять положення рівноваги. Такі коливання струни називаються стоячими хвилями.
Задачі для самостійного розв’язування
1. Знайти коливання струни із закріпленими кінцями x 0 і
x l , якщо посередині струна зволікається від положення рівноваги і
в момент t 0 відпускається без початкової швидкості. Правильність
рішення перевірити, вважаючи у відповіді задачі 1: C l .
|
|
2 |
2. Струна, закріплена на |
||
кінцях х=0 і х=l, має в початковий |
||
момент |
форму |
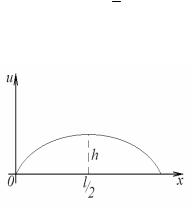
параболи |
u 4h/ 2 x x . |
Визначити |
|
зсув точок струни від осі абсцис, |
||
якщо |
початкові |
швидкості |
відсутні. (рис. 3.2).
Відповідь: |
|
|
|
|
|
|
Рисунок 3.2 |
|||||
u x, t 32h3 |
|
1 |
3 sin 2k |
1 |
x cos 2k |
1 at. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
2k 1 |
|
|
|
|
|
||||
Необхідно |
звернути |
|
увагу |
на |
той факт, |
що амплітуди |
||||||
послідовних гармонік тут убуває швидше, ніж в попередній задачі.
48
3. В початковому положенні струна знаходиться у спокої і точкам її на ділянці , додана постійна швидкість v 0 (цього можна добитися, ударяючи по струні на цій ділянці плоским жорстким молоточком). Знайти коливання струни. Досліджувати окремий випадок 0, .
Вказівка. Функція x представляється у вигляді:
0, |
|
если |
0 x ; |
|
, |
если |
x ; |
x v0 |
|||
|
|
если |
x . |
0, |
|
Відповідь:
|
|
|
2 v |
|
|
|
cos |
k |
|
cos |
k |
|
|
|
k |
k a |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
u x, t |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
sin |
|
x sin |
|
t; |
|||||||
|
|
2 |
a |
|
|
|
|
k |
2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
при 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
4 v |
0 |
|
|
|
1 |
|
|
|
|
|
|
2n 1 |
x |
|
|
2n 1 at |
|||||||||||
u x, t |
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
sin |
|
|
. |
|||||||
|
|
2 |
a |
|
2n 1 |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
4.Початкове відхилення струни, закріпленої в точках х = 0 і х
=l, рівні нулю, а початкова швидкість виражається формулою
49

u |
v0 const |
при |
|
x /2 |
|
h/2; |
|
|
|
|
|
|
x /2 |
|
|
t |
0 |
при |
|
|
h/2. |
||
|
|
|
|||||
Визначити форму струни для будь-якого моменту часу.
|
4v |
|
1 n |
|
|
|
2n 1 h |
|
|
2n 1 at |
|
|
2n 1 x |
||||||||||
U x,t |
|
0 |
|
|
|
|
sin |
|
|
|
|
sin |
|
|
|
|
sin |
|
|
|
|
||
|
2 |
|
2n 1 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|||||||||
|
a |
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
5. На |
відрізку 0 x , |
|
для рівняння utt |
a2uxx знайти |
|||||||||||||||||||
рішення за умов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
u 0,t u ,t 0, |
u x,0 0, |
ut x,0 sin |
2 x |
. |
|
|
|||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Відповідь: |
u x,t |
|
sin |
2 a |
t sin |
2 |
x. |
|
|
|
|
|
|
||||||||||
2 a |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6. Знайти закон коливання струни завдовжки l, розташованої на відрізку [0, ], якщо в початковий момент їй надали форму кривої
u |
x x |
, а потім відпустили без початкової швидкості. Струна |
|
8 |
|||
|
|
закріплена на кінцях. Зовнішні сили відсутні.
Відповідь:
|
|
|
|
1 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
2n 1 |
|
u x,t |
|
|
|
|
|
sin |
|
|
|
|
|
3 |
2n |
3 |
|
|
|
||||
|
|
n |
0 |
|
|
|
|
|||
cos 2n 1 at.
50
